Instantaneous Phase And Frequency

Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function:
:$\varphi(t) = \arg\,$
where arg is the complex argument function.
The instantaneous frequency is the 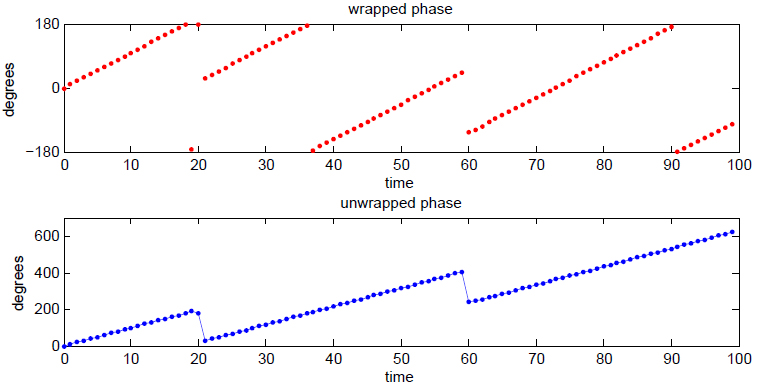temporal rate of change of the instantaneous phase.

And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''_a(''t''):
:\begin
\varphi(t) &= \arg\ \\ pt &= \arg\,
\end
where $\hat(t)$ represents the Hilbert transform of ''s''(''t'').

When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''_a(''t'') is a continuous function of ''t''. Unless otherwise indicated, the continuous form should be inferred.

Examples

Example 1

:$s(t) = A \cos(\omega t + \theta),$
where ''ω'' > 0.
:$\begin s_\mathrm(t) &= A e^, \\ \varphi(t) &= \omega t + \theta. \end$
In this simple sinusoidal example, the constant ''θ'' is also commonly referred to as ''phase'' or ''phase offset''. ''φ''(''t'') is a function of time; ''θ'' is not. In the next example, we also see that the phase offset of a real-valued sinusoid is ambiguous unless a reference (sin or cos) is specified. ''φ''(''t'') is unambiguously defined.

Example 2

:$s(t) = A \sin(\omega t) = A \cos\left(\omega t - \frac\right),$
where ''ω'' > 0.
:$\begin s_\mathrm(t) &= A e^, \\ \varphi(t) &= \omega t - \frac. \end$
In both examples the local maxima of ''s''(''t'') correspond to ''φ''(''t'') = 2''N'' for integer values of ''N''. This has applications in the field of computer vision.

Instantaneous frequency

Instantaneous angular frequency is defined as:
:$\omega(t) = \frac,$
and instantaneous (ordinary) frequency is defined as:
:$f(t) = \frac \omega(t) = \frac \frac$
where ''φ''(''t'') must be the unwrapped phase; otherwise, if ''φ''(''t'') is wrapped, discontinuities in ''φ''(''t'') will result in Dirac delta impulses in ''f''(''t'').

The inverse operation, which always unwraps phase, is:
:\begin
\varphi(t) &= \int_^t \omega(\tau)\, d\tau = 2 \pi \int_^t f(\tau)\, d\tau\\ pt &= \int_^0 \omega(\tau)\, d\tau + \int_0^t \omega(\tau)\, d\tau\\ pt &= \varphi(0) + \int_0^t \omega(\tau)\, d\tau.
\end

This instantaneous frequency, ''ω''(''t''), can be derived directly from the real and imaginary parts of ''s''_a(''t''), instead of the complex arg without concern of phase unwrapping.

:\begin
\varphi(t) &= \arg\ \\ pt &= \operatorname(\mathcal _\mathrm(t)\mathcal _\mathrm(t) + 2 m_1 \pi \\ pt &= \arctan\left( \frac \right) + m_2 \pi
\end

2''m''₁ and ''m''₂ are the integer multiples of necessary to add to unwrap the phase. At values of time, ''t'', where there is no change to integer ''m''₂, the derivative of ''φ''(''t'') is

:\begin
\omega(t) = \frac
&= \frac \arctan\left( \frac \right) \\ pt &= \frac \frac \left( \frac \right) \\ pt &= \frac \\ pt &= \frac \left(\mathcal _\mathrm(t)\frac - \mathcal _\mathrm(t)\frac \right) \\ pt &= \frac \left(s(t) \frac - \hat(t) \frac \right)
\end

For discrete-time functions, this can be written as a recursion:
:\begin
\varphi &= \varphi - 1+ \omega \\
&= \varphi - 1+ \underbrace_ \\
&= \varphi - 1+ \arg\left\ \\
\end

Discontinuities can then be removed by adding 2 whenever Δ''φ'' 'n''≤ −, and subtracting 2 whenever Δ''φ'' 'n''nbsp;> . That allows ''φ'' 'n''to accumulate without limit and produces an unwrapped instantaneous phase. An equivalent formulation that replaces the modulo 2 operation with a complex multiplication is:
:\varphi = \varphi - 1+ \arg\,
where the asterisk denotes complex conjugate. The discrete-time instantaneous frequency (in units of radians per sample) is simply the advancement of phase for that sample
:\omega = \arg\.

Complex representation

In some applications, such as averaging the values of phase at several moments of time, it may be useful to convert each value to a complex number, or vector representation:
:$e^ = \frac = \cos(\varphi(t)) + i \sin(\varphi(t)).$

This representation is similar to the wrapped phase representation in that it does not distinguish between multiples of 2 in the phase, but similar to the unwrapped phase representation since it is continuous. A vector-average phase can be obtained as the arg of the sum of the complex numbers without concern about wrap-around.

See also

* Analytic signal
* Frequency modulation
* Group delay
* Instantaneous amplitude
* Negative frequency

References

Further reading

*
*{{cite book , last1=Granlund , last2=Knutsson , title=Signal Processing for Computer Vision , publisher=Kluwer Academic Publishers , year=1995

Signal processing
Digital signal processing
Time–frequency analysis
Fourier analysis
Electrical engineering
Audio engineering