improper integrals

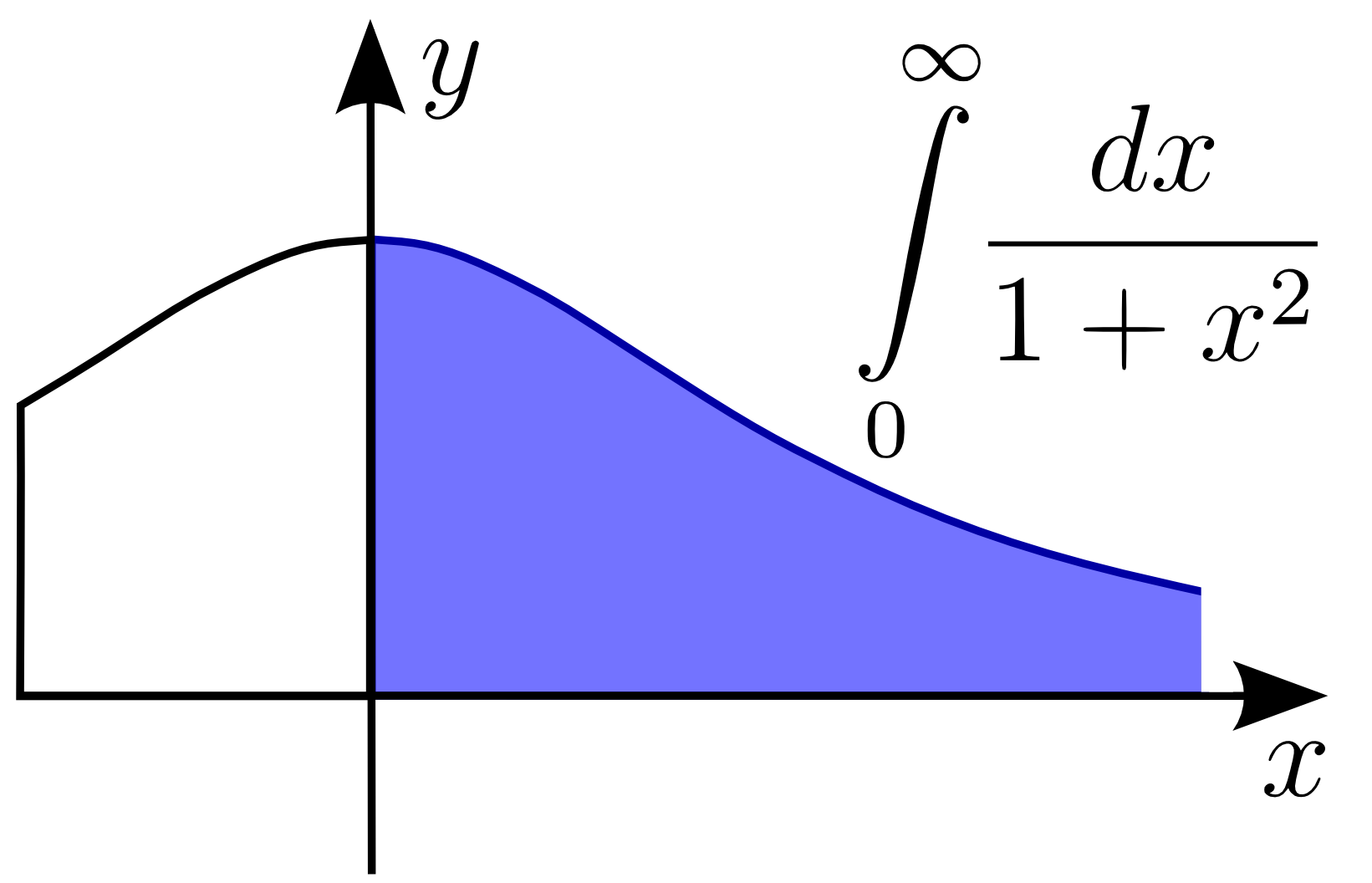
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result.

In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darboux) over a single interval, improper integrals may be in any of the following forms:
# $\int_a^\infty f(x)\, dx$
# $\int_^b f(x)\, dx$
# $\int_^\infty f(x)\, dx$
# $\int_a^b f(x)\, dx$, where $f(x)$ is undefined or discontinuous somewhere on ,b/math>

The first three forms are improper because the integrals are taken over an unbounded interval. (They may be improper for other reasons, as well, as explained below.) Such an integral is sometimes described as being of the "first" type or kind if the integrand otherwise satisfies the assumptions of integration. Integrals in the fourth form that are improper because $f(x)$ has a vertical asymptote somewhere on the interval ,b/math> may be described as being of the "second" type or kind. Integrals that combine aspects of both types are sometimes described as being of the "third" type or kind.

In each case above, the improper integral must be rewritten using one or more limits, depending on what is causing the integral to be improper. For example, in case 1, if $f(x)$ is continuous on the entire interval $[a,\infty)$, then
: $\int_a^\infty f(x)\, dx = \lim_ \int_a^b f(x)\, dx.$
The limit on the right is taken to be the definition of the integral notation on the left.

If $f(x)$ is only continuous on $(a,\infty)$ and not at $a$ itself, then typically this is rewritten as
: $\int_a^\infty f(x)\, dx = \lim_ \int_t^c f(x)\, dx + \lim_ \int_c^b f(x)\, dx,$
for any choice of $c>a$. Here both limits must converge to a finite value for the improper integral to be said to converge. This requirement avoids the ambiguous case of adding positive and negative infinities (i.e., the "$\infty-\infty$" indeterminate form). Alternatively, an iterated limit could be used or a single limit based on the Cauchy principal value.

If $f(x)$ is continuous on $[a,d)$ and $(d,\infty)$, with a discontinuity of any kind at $d$, then
: $\int_a^\infty f(x)\, dx = \lim_ \int_a^t f(x)\, dx + \lim_ \int_u^c f(x)\, dx + \lim_ \int_c^b f(x)\, dx,$
for any choice of $c>d$. The previous remarks about indeterminate forms, iterated limits, and the Cauchy principal value also apply here.

The function $f(x)$ can have more discontinuities, in which case even more limits would be required (or a more complicated principal value expression).

Cases 2–4 are handled similarly. See the examples below.

Improper integrals can also be evaluated in the context of complex numbers, in higher dimensions, and in other theoretical frameworks such as Lebesgue integration or Henstock–Kurzweil integration. Integrals that are considered improper in one framework may not be in others.

Examples

The original definition of the Riemann integral does not apply to a function such as $1/$ on the interval , because in this case the domain of integration is unbounded. However, the Riemann integral can often be extended by continuity, by defining the improper integral instead as a limit

:$\int_1^\infty \frac=\lim_ \int_1^b\frac = \lim_ \left(-\frac + \frac\right) = 1.$

The narrow definition of the Riemann integral also does not cover the function $1/\sqrt$ on the interval . The problem here is that the integrand is unbounded in the domain of integration. In other words, ''the definition of the Riemann integral requires that both the domain of integration and the integrand be bounded''. However, the improper integral does exist if understood as the limit

:$\int_0^1 \frac=\lim_\int_a^1\frac = \lim_ \left(2 - 2\sqrt\right)=2.$

Sometimes integrals may have two singularities where they are improper. Consider, for example, the function integrated from 0 to (shown right). At the lower bound of the integration domain, as goes to 0 the function goes to , and the upper bound is itself , though the function goes to 0. Thus this is a doubly improper integral. Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result of /6. To integrate from 1 to , a Riemann sum is not possible. However, any finite upper bound, say (with ), gives a well-defined result, . This has a finite limit as goes to infinity, namely /2. Similarly, the integral from 1/3 to 1 allows a Riemann sum as well, coincidentally again producing /6. Replacing 1/3 by an arbitrary positive value (with ) is equally safe, giving . This, too, has a finite limit as goes to zero, namely /2. Combining the limits of the two fragments, the result of this improper integral is
:$\begin \int_^ \frac & = \lim_ \int_s^1 \frac + \lim_ \int_1^t \frac \\ & = \lim_ \left(\frac - 2 \arctan \right) + \lim_ \left(2 \arctan - \frac \right) \\ & = \frac + \left(\pi - \frac \right) \\ & = \pi . \end$
This process does not guarantee success; a limit might fail to exist, or might be infinite. For example, over the bounded interval from 0 to 1 the integral of does not converge; and over the unbounded interval from 1 to the integral of does not converge.

It might also happen that an integrand is unbounded near an interior point, in which case the integral must be split at that point. For the integral as a whole to converge, the limit integrals on both sides must exist and must be bounded. For example:
:\begin
\int_^ \frac & = \lim_ \int_^ \frac
+ \lim_ \int_t^1 \frac \\
& = \lim_ 3\left(1-\sqrt right) + \lim_ 3\left(1-\sqrt right) \\
& = 3 + 3 \\
& = 6.
\end
But the similar integral
:$\int_^ \frac$
cannot be assigned a value in this way, as the integrals above and below zero in the integral domain do not independently converge. (However, see Cauchy principal value.)

Convergence of the integral

An improper integral converges if the limit defining it exists. Thus for example one says that the improper integral
:$\lim_\int_a^t f(x)\ dx$
exists and is equal to ''L'' if the integrals under the limit exist for all sufficiently large ''t'', and the value of the limit is equal to ''L''.

It is also possible for an improper integral to diverge to infinity. In that case, one may assign the value of ∞ (or −∞) to the integral. For instance
:$\lim_\int_1^b \frac = \infty.$
However, other improper integrals may simply diverge in no particular direction, such as
:$\lim_\int_1^b x\sin(x)\,dx,$
which does not exist, even as an extended real number. This is called divergence by oscillation.

A limitation of the technique of improper integration is that the limit must be taken with respect to one endpoint at a time. Thus, for instance, an improper integral of the form

:$\int_^\infty f(x)\,dx$

can be defined by taking two separate limits; to which

:$\int_^\infty f(x)\,dx = \lim_ \lim_ \int_a^bf(x)\,dx$

provided the double limit is finite. It can also be defined as a pair of distinct improper integrals of the first kind:

:$\lim_\int_a^c f(x)\,dx + \lim_ \int_c^b f(x)\,dx$

where ''c'' is any convenient point at which to start the integration. This definition also applies when one of these integrals is infinite, or both if they have the same sign.

An example of an improper integral where both endpoints are infinite is the Gaussian integral An example which evaluates to infinity is But one cannot even define other integrals of this kind unambiguously, such as since the double limit is infinite and the two-integral method

:$\lim_\int_a^cx\,dx + \lim_ \int_c^b x\,dx$
yields an indeterminate form, In this case, one can however define an improper integral in the sense of Cauchy principal value:

:$\operatorname \int_^\infty x\,dx = \lim_\int_^b x\,dx = 0.$

The questions one must address in determining an improper integral are:

*Does the limit exist?
*Can the limit be computed?

The first question is an issue of mathematical analysis. The second one can be addressed by calculus techniques, but also in some cases by contour integration, Fourier transforms and other more advanced methods.

Types of integrals

There is more than one theory of integration. From the point of view of calculus, the Riemann integral theory is usually assumed as the default theory. In using improper integrals, it can matter which integration theory is in play.

* For the Riemann integral (or the Darboux integral, which is equivalent to it), improper integration is necessary ''both'' for unbounded intervals (since one cannot divide the interval into finitely many subintervals of finite length) ''and'' for unbounded functions with finite integral (since, supposing it is unbounded above, then the upper integral will be infinite, but the lower integral will be finite).
* The Lebesgue integral deals differently with unbounded domains and unbounded functions, so that often an integral which only exists as an improper Riemann integral will exist as a (proper) Lebesgue integral, such as $\int_1^\infty \frac$. On the other hand, there are also integrals that have an improper Riemann integral but do not have a (proper) Lebesgue integral, such as $\int_0^\infty \frac\,dx$. The Lebesgue theory does not see this as a deficiency: from the point of view of measure theory, $\int_0^\infty \frac\,dx = \infty - \infty$ and cannot be defined satisfactorily. In some situations, however, it may be convenient to employ improper Lebesgue integrals as is the case, for instance, when defining the Cauchy principal value. The Lebesgue integral is more or less essential in the theoretical treatment of the Fourier transform, with pervasive use of integrals over the whole real line.
* For the Henstock–Kurzweil integral, improper integration ''is not necessary'', and this is seen as a strength of the theory: it encompasses all Lebesgue integrable and improper Riemann integrable functions.

Improper Riemann integrals and Lebesgue integrals

In some cases, the integral

:$\int_a^c f(x)\ dx$

can be defined as an integral (a Lebesgue integral, for instance) without reference to the limit

:$\lim_\int_a^b f(x)\,dx$

but cannot otherwise be conveniently computed. This often happens when the function ''f'' being integrated from ''a'' to ''c'' has a vertical asymptote at ''c'', or if ''c'' = ∞ (see Figures 1 and 2). In such cases, the improper Riemann integral allows one to calculate the Lebesgue integral of the function. Specifically, the following theorem holds :

* If a function ''f'' is Riemann integrable on 'a'',''b''for every ''b'' ≥ ''a'', and the partial integrals
::$\int_a^b, f(x), \,dx$
:are bounded as ''b'' → ∞, then the improper Riemann integrals
::$\int_a^\infty f(x)\,dx,\quad\mbox\int_a^\infty , f(x), \,dx$
:both exist. Furthermore, ''f'' is Lebesgue integrable on [''a'', ∞), and its Lebesgue integral is equal to its improper Riemann integral.

For example, the integral
:$\int_0^\infty\frac$
can be interpreted alternatively as the improper integral
:$\lim_\int_0^b\frac=\lim_\arctan=\frac,$
or it may be interpreted instead as a Lebesgue integral over the set (0, ∞). Since both of these kinds of integral agree, one is free to choose the first method to calculate the value of the integral, even if one ultimately wishes to regard it as a Lebesgue integral. Thus improper integrals are clearly useful tools for obtaining the actual values of integrals.

In other cases, however, a Lebesgue integral between finite endpoints may not even be defined, because the integrals of the positive and negative parts of ''f'' are both infinite, but the improper Riemann integral may still exist. Such cases are "properly improper" integrals, i.e. their values cannot be defined except as such limits. For example,

:$\int_0^\infty\frac\,dx$

cannot be interpreted as a Lebesgue integral, since

:$\int_0^\infty\left, \frac\\,dx=\infty.$

But $f(x)=\frac$ is nevertheless integrable between any two finite endpoints, and its integral between 0 and ∞ is usually understood as the limit of the integral:

:$\int_0^\infty\frac\,dx=\lim_\int_0^b\frac\,dx=\frac.$

Singularities

One can speak of the ''singularities'' of an improper integral, meaning those points of the extended real number line at which limits are used.

Cauchy principal value

Consider the difference in values of two limits:

:$\lim_\left(\int_^\frac+\int_a^1\frac\right)=0,$

:$\lim_\left(\int_^\frac+\int_^1\frac\right)=-\ln 2.$

The former is the Cauchy principal value of the otherwise ill-defined expression

:$\int_^1\frac \left(\mbox\ \mbox\ -\infty+\infty\right).$

Similarly, we have

:$\lim_\int_^a\frac=0,$

but

:$\lim_\int_^a\frac=-\ln 4.$

The former is the principal value of the otherwise ill-defined expression

:$\int_^\infty\frac \left(\mbox\ \mbox\ -\infty+\infty\right).$

All of the above limits are cases of the indeterminate form $\infty - \infty$.

These pathologies do not affect "Lebesgue-integrable" functions, that is, functions the integrals of whose absolute values are finite.

Summability

An improper integral may diverge in the sense that the limit defining it may not exist. In this case, there are more sophisticated definitions of the limit which can produce a convergent value for the improper integral. These are called summability methods.

One summability method, popular in Fourier analysis, is that of Cesàro summation. The integral

:$\int_0^\infty f(x)\,dx$

is Cesàro summable (C, α) if

:$\lim_\int_0^\lambda\left(1-\frac\right)^\alpha f(x)\ dx$

exists and is finite . The value of this limit, should it exist, is the (C, α) sum of the integral.

An integral is (C, 0) summable precisely when it exists as an improper integral. However, there are integrals which are (C, α) summable for α > 0 which fail to converge as improper integrals (in the sense of Riemann or Lebesgue). One example is the integral

:$\int_0^\infty\sin x \,dx$

which fails to exist as an improper integral, but is (C,''α'') summable for every ''α'' > 0. This is an integral version of Grandi's series.

Multivariable improper integrals

The improper integral can also be defined for functions of several variables. The definition is slightly different, depending on whether one requires integrating over an unbounded domain, such as $\R^2$, or is integrating a function with singularities, like $f(x,y)=\log\left(x^2+y^2\right)$.

Improper integrals over arbitrary domains

If $f:\R^n\to\R$ is a non-negative function that is Riemann integrable over every compact cube of the form a,an, for $a>0$, then the improper integral of ''f'' over $\R^n$ is defined to be the limit
:$\lim_\int_f,$
provided it exists.

A function on an arbitrary domain ''A'' in $\mathbb R^n$ is extended to a function $\tilde$ on $\R^n$ by zero outside of ''A'':
:$\tilde(x)=\beginf(x)& x\in A\\ 0 & x\not\in A \end$
The Riemann integral of a function over a bounded domain ''A'' is then defined as the integral of the extended function $\tilde$ over a cube a,an containing ''A'':
:$\int_A f = \int_\tilde.$
More generally, if ''A'' is unbounded, then the improper Riemann integral over an arbitrary domain in $\mathbb R^n$ is defined as the limit:
:$\int_Af=\lim_\int_f=\lim_\int_\tilde.$

Improper integrals with singularities

If ''f'' is a non-negative function which is unbounded in a domain ''A'', then the improper integral of ''f'' is defined by truncating ''f'' at some cutoff ''M'', integrating the resulting function, and then taking the limit as ''M'' tends to infinity. That is for $M>0$, set $f_M=\min\$. Then define
:$\int_A f = \lim_\int_A f_M$
provided this limit exists.

Functions with both positive and negative values

These definitions apply for functions that are non-negative. A more general function ''f'' can be decomposed as a difference of its positive part $f_+=\max\$ and negative part $f_-=\max\$, so
:$f=f_+-f_-$
with $f_+$ and $f_-$ both non-negative functions. The function ''f'' has an improper Riemann integral if each of $f_+$ and $f_-$ has one, in which case the value of that improper integral is defined by
:$\int_Af = \int_Af_+ - \int_A f_-.$
In order to exist in this sense, the improper integral necessarily converges absolutely, since
:$\int_A, f, = \int_Af_+ + \int_Af_-.$: "The relevant notion here is that of unconditional convergence." ... "In fact, for improper integrals of such functions, unconditional convergence turns out to be equivalent to absolute convergence."

Notes

Bibliography

* .
* .
*
* .
*
*

External links

Numerical Methods to Solve Improper Integrals
at Holistic Numerical Methods Institute

{{integral

Integral calculus