Heteroclinic bifurcation

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps).

The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them .

Bifurcation types

It is useful to divide bifurcations into two principal classes:
* Local bifurcations, which can be analysed entirely through changes in the local stability properties of equilibria, periodic orbits or other invariant sets as parameters cross through critical thresholds; and
* Global bifurcations, which often occur when larger invariant sets of the system 'collide' with each other, or with equilibria of the system. They cannot be detected purely by a stability analysis of the equilibria (fixed points).

Local bifurcations

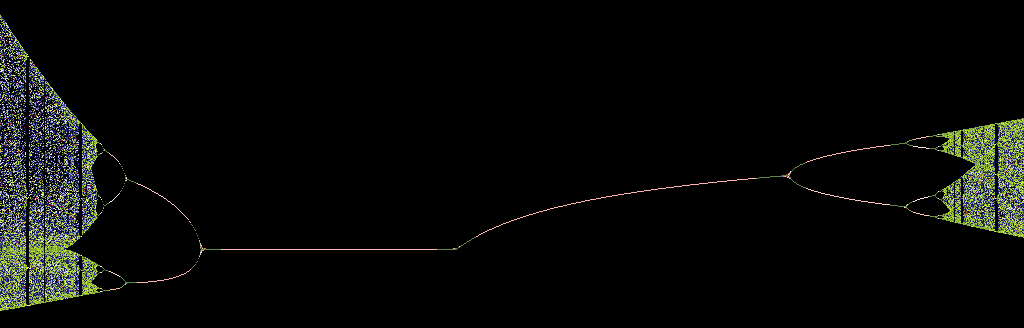A local bifurcation occurs when a parameter change causes the stability of an equilibrium (or fixed point) to change. In continuous systems, this corresponds to the real part of an eigenvalue of an equilibrium passing through zero. In discrete systems (described by maps), this corresponds to a fixed point having a Floquet multiplier with modulus equal to one. In both cases, the equilibrium is ''non-hyperbolic'' at the bifurcation point.
The topological changes in the phase portrait of the system can be confined to arbitrarily small neighbourhoods of the bifurcating fixed points by moving the bifurcation parameter close to the bifurcation point (hence 'local').

More technically, consider the continuous dynamical system described by the ordinary differential equation (ODE)
:$\dot x=f(x,\lambda)\quad f\colon\mathbb^n\times\mathbb\rightarrow\mathbb^n.$
A local bifurcation occurs at $(x_0,\lambda_0)$ if the Jacobian matrix
$\textrmf_$
has an eigenvalue with zero real part. If the eigenvalue is equal to zero, the bifurcation is a steady state bifurcation, but if the eigenvalue is non-zero but purely imaginary, this is a Hopf bifurcation.

For discrete dynamical systems, consider the system
:$x_=f(x_n,\lambda)\,.$
Then a local bifurcation occurs at $(x_0,\lambda_0)$ if the matrix
$\textrmf_$
has an eigenvalue with modulus equal to one. If the eigenvalue is equal to one, the bifurcation is either a saddle-node (often called fold bifurcation in maps), transcritical or pitchfork bifurcation. If the eigenvalue is equal to −1, it is a period-doubling (or flip) bifurcation, and otherwise, it is a Hopf bifurcation.

Examples of local bifurcations include:

* Saddle-node (fold) bifurcation
* Transcritical bifurcation
* Pitchfork bifurcation
* Period-doubling (flip) bifurcation
* Hopf bifurcation
* Neimark–Sacker (secondary Hopf) bifurcation

Global bifurcations

Global bifurcations occur when 'larger' invariant sets, such as periodic orbits, collide with equilibria. This causes changes in the topology of the trajectories in the phase space which cannot be confined to a small neighbourhood, as is the case with local bifurcations. In fact, the changes in topology extend out to an arbitrarily large distance (hence 'global').

Examples of global bifurcations include:

*Homoclinic bifurcation in which a limit cycle collides with a saddle point. Homoclinic bifurcations can occur supercritically or subcritically. The variant above is the "small" or "type I" homoclinic bifurcation. In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic dynamics.
*Heteroclinic bifurcation in which a limit cycle collides with two or more saddle points; they involve a heteroclinic cycle. Heteroclinic bifurcations are of two types: resonance bifurcations and transverse bifurcations. Both types of bifurcation will result in the change of stability of the heteroclinic cycle. At a resonance bifurcation, the stability of the cycle changes when an algebraic condition on the eigenvalues of the equilibria in the cycle is satisfied. This is usually accompanied by the birth or death of a periodic orbit. A transverse bifurcation of a heteroclinic cycle is caused when the real part of a transverse eigenvalue of one of the equilibria in the cycle passes through zero. This will also cause a change in stability of the heteroclinic cycle.
* Infinite-period bifurcation in which a stable node and saddle point simultaneously occur on a limit cycle. As the limit of a parameter approaches a certain critical value, the speed of the oscillation slows down and the period approaches infinity. The infinite-period bifurcation occurs at this critical value. Beyond the critical value, the two fixed points emerge continuously from each other on the limit cycle to disrupt the oscillation and form two saddle points.
* Blue sky catastrophe in which a limit cycle collides with a nonhyperbolic cycle.

Global bifurcations can also involve more complicated sets such as chaotic attractors (e.g. crises).

Codimension of a bifurcation

The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. This corresponds to the codimension of the parameter set for which the bifurcation occurs within the full space of parameters. Saddle-node bifurcations and Hopf bifurcations are the only generic local bifurcations which are really codimension-one (the others all having higher codimension). However, transcritical and pitchfork bifurcations are also often thought of as codimension-one, because the normal forms can be written with only one parameter.

An example of a well-studied codimension-two bifurcation is the Bogdanov–Takens bifurcation.

Applications in semiclassical and quantum physics

Bifurcation theory has been applied to connect quantum systems to the dynamics of their classical analogues in atomic systems, molecular systems, and resonant tunneling diodes. Bifurcation theory has also been applied to the study of laser dynamics and a number of theoretical examples which are difficult to access experimentally such as the kicked top and coupled quantum wells. The dominant reason for the link between quantum systems and bifurcations in the classical equations of motion is that at bifurcations, the signature of classical orbits becomes large, as Martin Gutzwiller points out in his classic work on quantum chaos. Many kinds of bifurcations have been studied with regard to links between classical and quantum dynamics including saddle node bifurcations, Hopf bifurcations, umbilic bifurcations, period doubling bifurcations, reconnection bifurcations, tangent bifurcations, and cusp bifurcations.

See also

* Bifurcation diagram
* Bifurcation memory
* Catastrophe theory
* Feigenbaum constants
* Geomagnetic reversal
* Phase portrait
* Tennis racket theorem

Notes

References

*
*Guardia, M.; Martinez-Seara, M.; Teixeira, M. A. (2011)
Generic bifurcations of low codimension of planar Filippov Systems
"Journal of differential equations", Febrer 2011, vol. 250, núm. 4, pp. 1967–2023. DOI:10.1016/j.jde.2010.11.016
*

External links

Nonlinear dynamics

Bifurcations and Two Dimensional Flows
by Elmer G. Wiens

Introduction to Bifurcation theory
by John David Crawford

{{DEFAULTSORT:Bifurcation Theory

Nonlinear systems