|
Heteroclinic Cycle
In mathematics, a heteroclinic cycle is an invariant set in the phase space of a dynamical system. It is a topological circle of equilibrium points and connecting heteroclinic orbits. If a heteroclinic cycle is asymptotically stable, approaching trajectories spend longer and longer periods of time in a neighbourhood of successive equilibria. In generic dynamical systems heteroclinic connections are of high co-dimension, that is, they will not persist if parameters are varied. Robust heteroclinic cycles A robust heteroclinic cycle is one which persists under small changes in the underlying dynamical system. Robust cycles often arise in the presence of symmetry or other constraints which force the existence of invariant hyperplanes. A prototypical example of a robust heteroclinic cycle is the Guckenheimer–Holmes cycle. This cycle has also been studied in the context of rotating convection, and as three competing species in population dynamics. See also * Heteroclinic b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Point
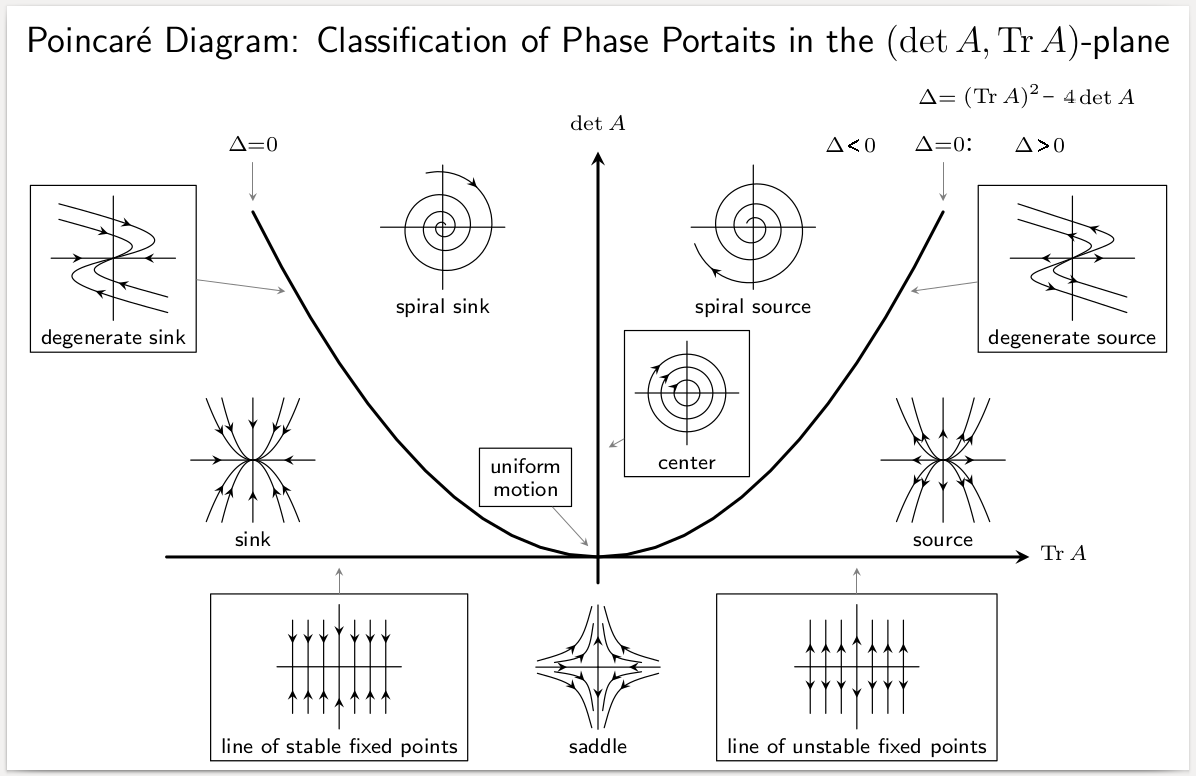
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroclinic Orbit
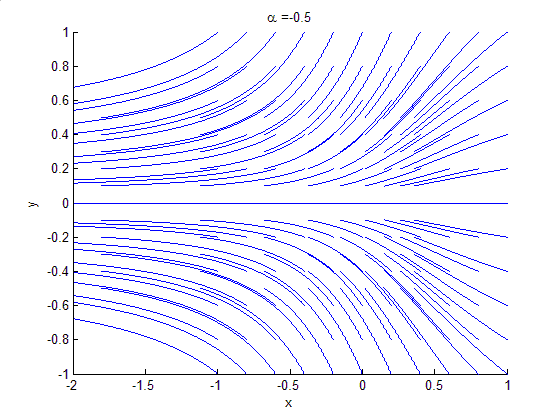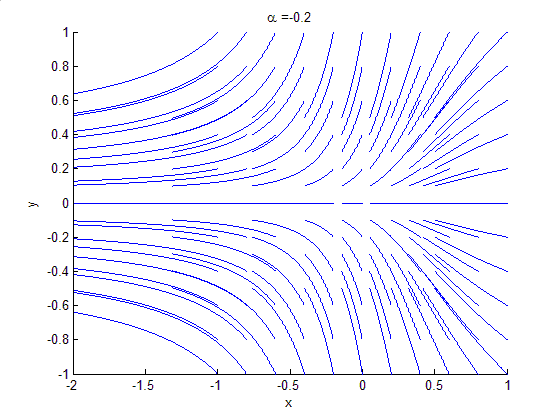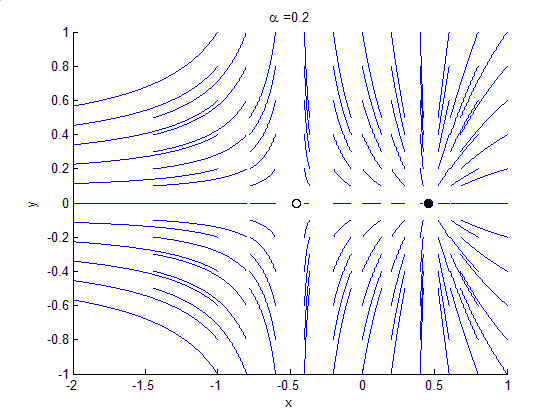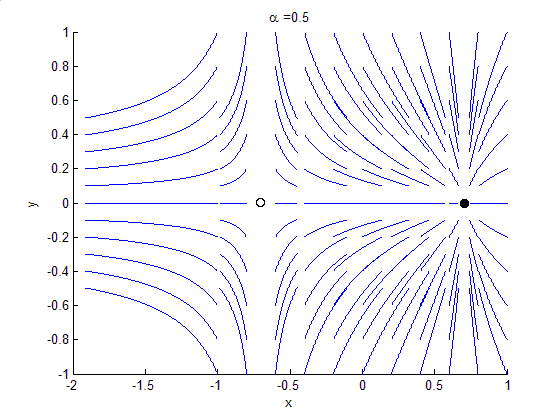
In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit (sometimes called a heteroclinic connection) is a path in phase space which joins two different equilibrium points. If the equilibrium points at the start and end of the orbit are the same, the orbit is a homoclinic orbit. Consider the continuous dynamical system described by the ODE ::\dot x=f(x) Suppose there are equilibria at x=x_0 and x=x_1, then a solution \phi(t) is a heteroclinic orbit from x_0 to x_1 if ::\phi(t)\rightarrow x_0\quad \mathrm\quad t\rightarrow-\infty and ::\phi(t)\rightarrow x_1\quad \mathrm\quad t\rightarrow+\infty This implies that the orbit is contained in the stable manifold of x_1 and the unstable manifold of x_0. Symbolic dynamics By using the Markov partition, the long-time behaviour of hyperbolic system can be studied using the techniques of symbolic dynamics. In this case, a heteroclinic orbit has a particularly simple and clear representation. Suppose that S=\ is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroclinic Bifurcation
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can be ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroclinic Network
In mathematics, a heteroclinic network is an invariant set in the phase space of a dynamical system. It can be thought of loosely as the union of more than one heteroclinic cycle In mathematics, a heteroclinic cycle is an invariant set in the phase space of a dynamical system. It is a topological circle of equilibrium points and connecting heteroclinic orbits. If a heteroclinic cycle is asymptotically stable, approaching t .... Heteroclinic networks arise naturally in a number of different types of applications, including fluid dynamics and populations dynamics. The dynamics of trajectories near to heteroclinic networks is intermittent: trajectories spend a long time performing one type of behaviour (often, close to equilibrium), before switching rapidly to another type of behaviour. This type of intermittent switching behaviour has led to several different groups of researchers using them as ways to model and understand various type of neural dynamics. References * * * * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Guckenheimer
John Mark Guckenheimer (born 1945) joined the Department of Mathematics at Cornell University in 1985. He was previously at the University of California, Santa Cruz (1973-1985). He was a Guggenheim fellow in 1984, and was elected president of the Society for Industrial and Applied Mathematics (SIAM), serving from 1997 to 1998. Guckenheimer received his A.B. in 1966 from Harvard and his Ph.D. in 1970 from Berkeley, where his Ph.D. thesis advisor was Stephen Smale. His book ''Nonlinear Oscillations, Dynamical Systems and Bifurcation of Vector Fields'' (with Philip Holmes) is an extensively cited work on dynamical systems. Research Dr. John Guckenheimer's research has focused on three areas — neuroscience, algorithms for periodic orbits, and dynamics in systems with multiple time scales. Neuroscience Guckenheimer studies dynamical models of a small neural system, the stomatogastric ganglion of crustaceans — attempting to learn more about neuromodulation, the ways in which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip Holmes
Philip John Holmes (born May 24, 1945) is the Eugene Higgins Professor of Mechanical and Aerospace Engineering at Princeton University. As a member of the Mechanical and Aerospace Engineering department, he formerly served as the interim chair until May 2007. Before moving to Princeton in 1994 he taught theoretical and applied mechanics at Cornell University from 1977 until 1994, when he was the Charles N. Mellowes Professor of Engineering and Professor of Mathematics. Holmes was educated in England at the University of Oxford, where he studied engineering from 1964 to 1967, and at the University of Southampton, where he obtained a Ph.D. in engineering in 1974. He has made solid contributions to the field of nonlinear dynamics and differential equations. His book on dynamical systems with John Guckenheimer is a landmark in the field. Holmes is a very creative researcher and scientist and an outstanding lecturer. The sheer breadth of his contributions to applied mathematics i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |