Great Truncated Cuboctahedron on:
[Wikipedia]
[Google]
[Amazon]
 In
In
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, the great truncated cuboctahedron (or quasitruncated cuboctahedron or stellatruncated cuboctahedron) is a nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, ...
, indexed as U20. It has 26 faces (12 square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
s, 8 hexagon
In geometry, a hexagon (from Ancient Greek, Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple polygon, simple (non-self-intersecting) hexagon is 720°.
Regular hexa ...
s and 6 octagram
In geometry, an octagram is an eight-angled star polygon.
The name ''octagram'' combine a Greek numeral prefix, '' octa-'', with the Greek suffix '' -gram''. The ''-gram'' suffix derives from γραμμή (''grammḗ'') meaning "line".
Detai ...
s), 72 edges, and 48 vertices. It is represented by the Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
tr, and Coxeter-Dynkin diagram . It is sometimes called the quasitruncated cuboctahedron because it is related to the truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its fac ...
, , except that the octagonal faces are replaced by octagrams.
Convex hull
Itsconvex hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space ...
is a nonuniform truncated cuboctahedron
In geometry, the truncated cuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its fac ...
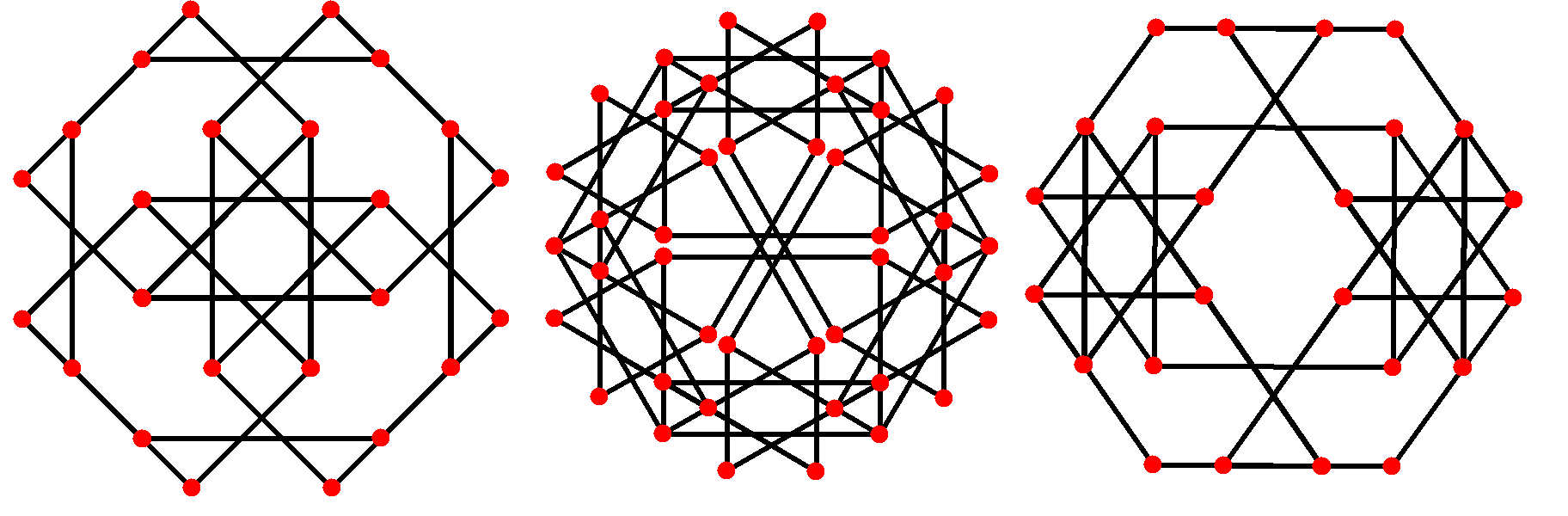
. The truncated cuboctahedron and the great truncated cuboctahedron form isomorphic graphs despite their different geometric structure.
Orthographic projections

Cartesian coordinates
Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
for the vertices of a great truncated cuboctahedron centered at the origin are all permutations of
See also
*List of uniform polyhedra
In geometry, a uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive ( transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are c ...
References
External links
* Uniform polyhedra {{Polyhedron-stub