Gravitational perturbation on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Most systems that involve multiple gravitational attractions present one primary body which is dominant in its effects (for example, a star, in the case of the star and its planet, or a planet, in the case of the planet and its satellite). The gravitational effects of the other bodies can be treated as perturbations of the hypothetical unperturbed motion of the planet or
Most systems that involve multiple gravitational attractions present one primary body which is dominant in its effects (for example, a star, in the case of the star and its planet, or a planet, in the case of the planet and its satellite). The gravitational effects of the other bodies can be treated as perturbations of the hypothetical unperturbed motion of the planet or
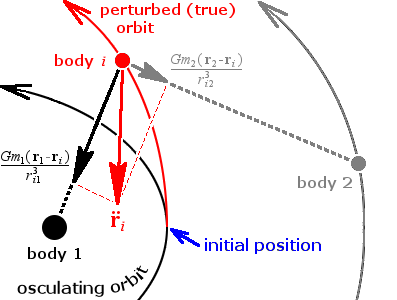 Cowell's formulation (so named for Philip H. Cowell, who, with A.C.D. Cromellin, used a similar method to predict the return of Halley's comet) is perhaps the simplest of the special perturbation methods. In a system of mutually interacting bodies, this method mathematically solves for the Newtonian forces on body by summing the individual interactions from the other bodies:
:
where is the
Cowell's formulation (so named for Philip H. Cowell, who, with A.C.D. Cromellin, used a similar method to predict the return of Halley's comet) is perhaps the simplest of the special perturbation methods. In a system of mutually interacting bodies, this method mathematically solves for the Newtonian forces on body by summing the individual interactions from the other bodies:
:
where is the
 Encke's method begins with the
Encke's method begins with the
 In the Solar System, many of the disturbances of one planet by another are periodic, consisting of small impulses each time a planet passes another in its orbit. This causes the bodies to follow motions that are periodic or quasi-periodic – such as the Moon in its strongly perturbed
In the Solar System, many of the disturbances of one planet by another are periodic, consisting of small impulses each time a planet passes another in its orbit. This causes the bodies to follow motions that are periodic or quasi-periodic – such as the Moon in its strongly perturbed
Introduction to the Theory of Flight of Artificial Earth Satellites
(by Aldo Vitagliano) predictions for the position/orbit/close approaches of Mars
Gravitation
Sir George Biddell Airy's 1884 book on gravitational motion and perturbations, using little or no math.(a
Google books
{{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System * Dynamical systems Dynamics of the Solar System Celestial mechanics
astronomy
Astronomy () is a natural science that studies celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and evolution. Objects of interest include planets, moons, stars, nebulae, g ...
, perturbation is the complex motion of a massive body subjected to forces other than the gravitational
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stron ...
attraction of a single other mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
ive body
Body may refer to:
In science
* Physical body, an object in physics that represents a large amount, has mass or takes up space
* Body (biology), the physical material of an organism
* Body plan, the physical features shared by a group of anima ...
. The other forces can include a third (fourth, fifth, etc.) body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body.
Introduction
The study of perturbations began with the first attempts to predict planetary motions in the sky. In ancient times the causes were unknown.Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the grea ...
, at the time he formulated his laws of motion
In physics, motion is the phenomenon in which an object changes its position with respect to time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed and frame of reference to an observer and m ...
and of gravitation, applied them to the first analysis of perturbations, recognizing the complex difficulties of their calculation. Many of the great mathematicians since then have given attention to the various problems involved; throughout the 18th and 19th centuries there was demand for accurate tables of the position of the Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width of ...
and planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a you ...
s for marine navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
.
The complex motions of gravitational perturbations can be broken down. The hypothetical motion that the body follows under the gravitational effect of one other body only is a conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a spe ...
, and can be described in geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ...
terms. This is called a two-body problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each ...
, or an unperturbed Keplerian orbit
Johannes Kepler (; ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws ...
. The differences between that and the actual motion of the body are perturbations due to the additional gravitational effects of the remaining body or bodies. If there is only one other significant body then the perturbed motion is a three-body problem
In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's ...
; if there are multiple other bodies it is an ''n''-body problem. A general analytical solution (a mathematical expression to predict the positions and motions at any future time) exists for the two-body problem; when more than two bodies are considered analytic solutions exist only for special cases. Even the two-body problem becomes insoluble if one of the bodies is irregular in shape.Roy (1988): ch. 6, 7.
 Most systems that involve multiple gravitational attractions present one primary body which is dominant in its effects (for example, a star, in the case of the star and its planet, or a planet, in the case of the planet and its satellite). The gravitational effects of the other bodies can be treated as perturbations of the hypothetical unperturbed motion of the planet or
Most systems that involve multiple gravitational attractions present one primary body which is dominant in its effects (for example, a star, in the case of the star and its planet, or a planet, in the case of the planet and its satellite). The gravitational effects of the other bodies can be treated as perturbations of the hypothetical unperturbed motion of the planet or satellite
A satellite or artificial satellite is an object intentionally placed into orbit in outer space. Except for passive satellites, most satellites have an electricity generation system for equipment on board, such as solar panels or radioi ...
around its primary body.
Mathematical analysis
General perturbations
In methods of general perturbations, general differential equations, either of motion or of change in the orbital elements, are solved analytically, usually byseries expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and divisi ...
s. The result is usually expressed in terms of algebraic and trigonometric functions of the orbital elements of the body in question and the perturbing bodies. This can be applied generally to many different sets of conditions, and is not specific to any particular set of gravitating objects. Historically, general perturbations were investigated first. The classical methods are known as ''variation of the elements'', ''variation of parameters
In mathematics, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous linear ordinary differential equations.
For first-order inhomogeneous linear differential equations it is usually possible t ...
'' or ''variation of the constants of integration''. In these methods, it is considered that the body is always moving in a conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a spe ...
, however the conic section is constantly changing due to the perturbations. If all perturbations were to cease at any particular instant, the body would continue in this (now unchanging) conic section indefinitely; this conic is known as the osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if pertu ...
and its orbital elements at any particular time are what are sought by the methods of general perturbations.
General perturbations takes advantage of the fact that in many problems of celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, the two-body orbit changes rather slowly due to the perturbations; the two-body orbit is a good first approximation. General perturbations is applicable only if the perturbing forces are about one order of magnitude smaller, or less, than the gravitational force of the primary body. In the Solar System
The Solar System Capitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar ...
, this is usually the case; Jupiter
Jupiter is the fifth planet from the Sun and the largest in the Solar System. It is a gas giant with a mass more than two and a half times that of all the other planets in the Solar System combined, but slightly less than one-thousandth t ...
, the second largest body, has a mass of about 1/1000 that of the Sun
The Sun is the star at the center of the Solar System. It is a nearly perfect ball of hot plasma, heated to incandescence by nuclear fusion reactions in its core. The Sun radiates this energy mainly as light, ultraviolet, and infrared radi ...
.
General perturbation methods are preferred for some types of problems, as the source of certain observed motions are readily found. This is not necessarily so for special perturbations; the motions would be predicted with similar accuracy, but no information on the configurations of the perturbing bodies (for instance, an orbital resonance
In celestial mechanics, orbital resonance occurs when orbiting bodies exert regular, periodic gravitational influence on each other, usually because their orbital periods are related by a ratio of small integers. Most commonly, this relationsh ...
) which caused them would be available.
Special perturbations
In methods of special perturbations, numerical datasets, representing values for the positions, velocities and accelerative forces on the bodies of interest, are made the basis ofnumerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations ...
of the differential equations of motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.''Encyclopaedia of Physics'' (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Ver ...
. In effect, the positions and velocities are perturbed directly, and no attempt is made to calculate the curves of the orbits or the orbital elements.Moulton (1914): ch. IX
Special perturbations can be applied to any problem in celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, as it is not limited to cases where the perturbing forces are small. Once applied only to comets and minor planets, special perturbation methods are now the basis of the most accurate machine-generated planetary ephemerides of the great astronomical almanacs. Special perturbations are also used for modeling
A model is an informative representation of an object, person or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin ''modulus'', a measure.
Models c ...
an orbit with computers.
Cowell's formulation
 Cowell's formulation (so named for Philip H. Cowell, who, with A.C.D. Cromellin, used a similar method to predict the return of Halley's comet) is perhaps the simplest of the special perturbation methods. In a system of mutually interacting bodies, this method mathematically solves for the Newtonian forces on body by summing the individual interactions from the other bodies:
:
where is the
Cowell's formulation (so named for Philip H. Cowell, who, with A.C.D. Cromellin, used a similar method to predict the return of Halley's comet) is perhaps the simplest of the special perturbation methods. In a system of mutually interacting bodies, this method mathematically solves for the Newtonian forces on body by summing the individual interactions from the other bodies:
:
where is the acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by t ...
vector of body , is the gravitational constant, is the mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
of body , and are the position vectors of objects and respectively, and is the distance from object to object , all vectors being referred to the barycenter
In astronomy, the barycenter (or barycentre; ) is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important con ...
of the system. This equation is resolved into components in , , and and these are integrated numerically to form the new velocity and position vectors. This process is repeated as many times as necessary. The advantage of Cowell's method is ease of application and programming. A disadvantage is that when perturbations become large in magnitude (as when an object makes a close approach to another) the errors of the method also become large.
, chapter 11.
However, for many problems in celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, this is never the case. Another disadvantage is that in systems with a dominant central body, such as the Sun
The Sun is the star at the center of the Solar System. It is a nearly perfect ball of hot plasma, heated to incandescence by nuclear fusion reactions in its core. The Sun radiates this energy mainly as light, ultraviolet, and infrared radi ...
, it is necessary to carry many significant digits
Significant figures (also known as the significant digits, ''precision'' or ''resolution'') of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something.
If a number expre ...
in the arithmetic because of the large difference in the forces of the central body and the perturbing bodies, although with modern computers this is not nearly the limitation it once was.
Encke's method
osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if pertu ...
as a reference and integrates numerically to solve for the variation from the reference as a function of time.
Its advantages are that perturbations are generally small in magnitude, so the integration can proceed in larger steps (with resulting lesser errors), and the method is much less affected by extreme perturbations. Its disadvantage is complexity; it cannot be used indefinitely without occasionally updating the osculating orbit and continuing from there, a process known as ''rectification''. Encke's method is similar to the general perturbation method of variation of the elements, except the rectification is performed at discrete intervals rather than continuously.
Letting be the radius vector of the osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if pertu ...
, the radius vector of the perturbed orbit, and the variation from the osculating orbit,
and are just the equations of motion of and
where is the gravitational parameter
In celestial mechanics, the standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of the bodies. For two bodies the parameter may be expressed as G(m1+m2), or as GM when ...
with and the mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
es of the central body and the perturbed body, is the perturbing acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by t ...
, and and are the magnitudes of and .
Substituting from equations () and () into equation (),
which, in theory, could be integrated twice to find . Since the osculating orbit is easily calculated by two-body methods, and are accounted for and can be solved. In practice, the quantity in the brackets, , is the difference of two nearly equal vectors, and further manipulation is necessary to avoid the need for extra significant digits
Significant figures (also known as the significant digits, ''precision'' or ''resolution'') of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something.
If a number expre ...
.
Encke's method was more widely used before the advent of modern computers, when much orbit computation was performed on mechanical calculating machines.
Periodic nature
 In the Solar System, many of the disturbances of one planet by another are periodic, consisting of small impulses each time a planet passes another in its orbit. This causes the bodies to follow motions that are periodic or quasi-periodic – such as the Moon in its strongly perturbed
In the Solar System, many of the disturbances of one planet by another are periodic, consisting of small impulses each time a planet passes another in its orbit. This causes the bodies to follow motions that are periodic or quasi-periodic – such as the Moon in its strongly perturbed orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a p ...
, which is the subject of lunar theory Lunar theory attempts to account for the motions of the Moon. There are many small variations (or perturbations) in the Moon's motion, and many attempts have been made to account for them. After centuries of being problematic, lunar motion can now ...
. This periodic nature led to the discovery of Neptune
The planet Neptune was mathematically predicted before it was directly observed. With a prediction by Urbain Le Verrier, telescopic observations confirming the existence of a major planet were made on the night of September 23–24, 1846, at the ...
in 1846 as a result of its perturbations of the orbit of Uranus
Uranus is the seventh planet from the Sun. Its name is a reference to the Greek god of the sky, Uranus (mythology), Uranus (Caelus), who, according to Greek mythology, was the great-grandfather of Ares (Mars (mythology), Mars), grandfather ...
.
On-going mutual perturbations of the planets cause long-term quasi-periodic variations in their orbital element
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same ...
s, most apparent when two planets' orbital periods are nearly in sync. For instance, five orbits of Jupiter
Jupiter is the fifth planet from the Sun and the largest in the Solar System. It is a gas giant with a mass more than two and a half times that of all the other planets in the Solar System combined, but slightly less than one-thousandth t ...
(59.31 years) is nearly equal to two of Saturn
Saturn is the sixth planet from the Sun and the second-largest in the Solar System, after Jupiter. It is a gas giant with an average radius of about nine and a half times that of Earth. It has only one-eighth the average density of Earth; h ...
(58.91 years). This causes large perturbations of both, with a period of 918 years, the time required for the small difference in their positions at conjunction
Conjunction may refer to:
* Conjunction (grammar), a part of speech
* Logical conjunction, a mathematical operator
** Conjunction introduction, a rule of inference of propositional logic
* Conjunction (astronomy), in which two astronomical bodies ...
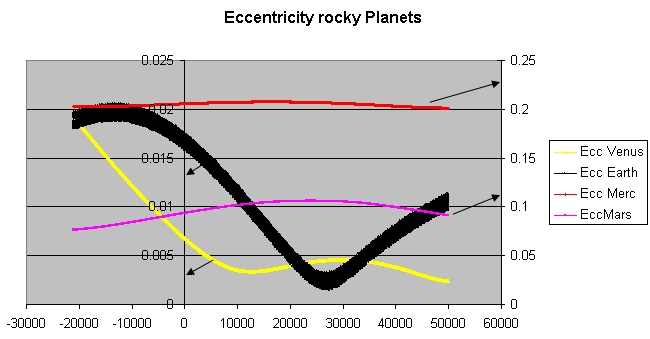
to make one complete circle, first discovered by Laplace. Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never fa ...
currently has the orbit with the least eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
, i.e. it is the closest to circular
Circular may refer to:
* The shape of a circle
* ''Circular'' (album), a 2006 album by Spanish singer Vega
* Circular letter (disambiguation)
** Flyer (pamphlet), a form of advertisement
* Circular reasoning, a type of logical fallacy
* Circula ...
, of all the planetary orbits. In 25,000 years' time, Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
will have a more circular (less eccentric) orbit than Venus. It has been shown that long-term periodic disturbances within the Solar System
The Solar System Capitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar ...
can become chaotic over very long time scales; under some circumstances one or more planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a you ...
s can cross the orbit of another, leading to collisions.see references at Stability of the Solar System
The stability of the Solar System is a subject of much inquiry in astronomy. Though the planets have been stable when historically observed, and will be in the short term, their weak gravitational effects on one another can add up in unpredictable ...
The orbits of many of the minor bodies of the Solar System, such as comet
A comet is an icy, small Solar System body that, when passing close to the Sun, warms and begins to release gases, a process that is called outgassing. This produces a visible atmosphere or coma, and sometimes also a tail. These phenomena ar ...
s, are often heavily perturbed, particularly by the gravitational fields of the gas giant
A gas giant is a giant planet composed mainly of hydrogen and helium. Gas giants are also called failed stars because they contain the same basic elements as a star. Jupiter and Saturn are the gas giants of the Solar System. The term "gas giant" ...
s. While many of these perturbations are periodic, others are not, and these in particular may represent aspects of chaotic motion
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have ...
. For example, in April 1996, Jupiter
Jupiter is the fifth planet from the Sun and the largest in the Solar System. It is a gas giant with a mass more than two and a half times that of all the other planets in the Solar System combined, but slightly less than one-thousandth t ...
's gravitational influence caused the period
Period may refer to:
Common uses
* Era, a length or span of time
* Full stop (or period), a punctuation mark
Arts, entertainment, and media
* Period (music), a concept in musical composition
* Periodic sentence (or rhetorical period), a concept ...
of Comet Hale–Bopp
Comet Hale–Bopp (formally designated C/1995 O1) is a comet that was one of the most widely observed of the 20th century and one of the brightest seen for many decades.
Alan Hale and Thomas Bopp discovered Comet Hale–Bopp separately ...
's orbit to decrease from 4,206 to 2,380 years, a change that will not revert on any periodic basis.
See also
*Formation and evolution of the Solar System
The formation of the Solar System began about 4.6 billion years ago with the gravitational collapse of a small part of a giant molecular cloud. Most of the collapsing mass collected in the center, forming the Sun, while the rest flattened into a ...
* Frozen orbit
In orbital mechanics, a frozen orbit is an orbit for an artificial satellite in which natural drifting due to the central body's shape has been minimized by careful selection of the orbital parameters. Typically, this is an orbit in which, over a ...
* Molniya orbit
A Molniya orbit ( rus, Молния, p=ˈmolnʲɪjə, a=Ru-молния.ogg, "Lightning") is a type of satellite orbit designed to provide communications and remote sensing coverage over high latitudes. It is a highly elliptical orbit with an ...
* Nereid
In Greek mythology, the Nereids or Nereides ( ; grc, Νηρηΐδες, Nērēḯdes; , also Νημερτές) are sea nymphs (female spirits of sea waters), the 50 daughters of the 'Old Man of the Sea' Nereus and the Oceanids, Oceanid Doris ...
one of the outer moons of Neptune with a high orbital eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values betwee ...
of ~0.75 and is frequently perturbed
* Osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space at a given moment in time is the gravitational Kepler orbit (i.e. an elliptic or other conic one) that it would have around its central body if perturba ...
* Orbit modeling
* Orbital resonance
In celestial mechanics, orbital resonance occurs when orbiting bodies exert regular, periodic gravitational influence on each other, usually because their orbital periods are related by a ratio of small integers. Most commonly, this relationsh ...
* Proper orbital elements
__NOTOC__
The proper orbital elements or proper elements of an orbit are constants of motion of an object in space that remain practically unchanged over an astronomically long timescale. The term is usually used to describe the three quantitie ...
* Stability of the Solar System
The stability of the Solar System is a subject of much inquiry in astronomy. Though the planets have been stable when historically observed, and will be in the short term, their weak gravitational effects on one another can add up in unpredictable ...
References
;Bibliography * * * ;FootnotesFurther reading
* P.E. El'YasbergIntroduction to the Theory of Flight of Artificial Earth Satellites
External links
(by Aldo Vitagliano) predictions for the position/orbit/close approaches of Mars
Gravitation
Sir George Biddell Airy's 1884 book on gravitational motion and perturbations, using little or no math.(a
Google books
{{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System * Dynamical systems Dynamics of the Solar System Celestial mechanics