|
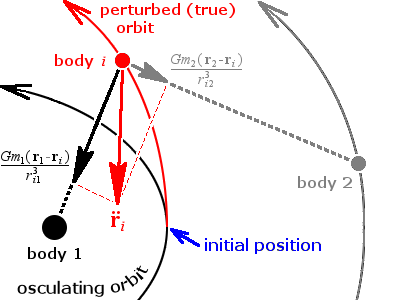
Orbit Modeling
Orbit modeling is the process of creating mathematical models to simulate motion of a massive body as it moves in orbit around another massive body due to gravity. Other forces such as gravitational attraction from tertiary bodies, air resistance, solar pressure, or thrust from a propulsion system are typically modeled as secondary effects. Directly modeling an orbit can push the limits of machine precision due to the need to model small perturbations to very large orbits. Because of this, perturbation methods are often used to model the orbit in order to achieve better accuracy. Background The study of orbital motion and mathematical modeling of orbits began with the first attempts to predict planetary motions in the sky, although in ancient times the causes remained a mystery. Newton, at the time he formulated his laws of motion and of gravitation, applied them to the first analysis of perturbations, recognizing the complex difficulties of their calculation. Many of the great ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics of orbi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modeling And Simulation
Modeling and simulation (M&S) is the use of models (e.g., physical, mathematical, or logical representation of a system, entity, phenomenon, or process) as a basis for simulations to develop data utilized for managerial or technical decision making. In the computer application of modeling and simulation a computer is used to build a mathematical model which contains key parameters of the physical model. The mathematical model represents the physical model in virtual form, and conditions are applied that set up the experiment of interest. The simulation starts – i.e., the computer calculates the results of those conditions on the mathematical model – and outputs results in a format that is either machine- or human-readable, depending upon the implementation. The use of M&S within engineering is well recognized. Simulation technology belongs to the tool set of engineers of all application domains and has been included in the body of knowledge of engineering management. M&S helps ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration (change of velocity) when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies. The SI base unit of mass is the kilogram (kg). In physics, mass is not the same as weight, even though mass is often determined by measuring the object's weight using a spring scale, rather than balance scale comparing it directly with known masses. An object on the Moon would weigh le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by the orientation of the ''net'' force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes: * the net balance of all external forces acting onto that object — magnitude is directly proportional to this net resulting force; * that object's mass, depending on the materials out of which it is made — magnitude is inversely proportional to the object's mass. The SI unit for acceleration is metre per second squared (, \mathrm). For example, when a vehicle starts from a standstill (zero velocity, in an inertial frame of reference) and travels in a straight line at increasing speeds, it is accelerating in the direction of travel. If the vehicle turns, an acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip Herbert Cowell
Philip Herbert Cowell FRS (1870 – 1949) was a British astronomer. Philip Herbert Cowell was born in Calcutta, India on the 7 August 1870, and educated at Eton and Trinity College, Cambridge. He became second chief assistant at the Royal Greenwich Observatory in 1896 and later became the Superintendent of HM Nautical Almanac Office between 1910 and 1930. He worked on celestial mechanics, and orbits of comets and minor planets in particular. He also carefully studied the discrepancy that then existed between the theory and observation of the position of the Moon. Cowell was elected a Fellow of the Royal Astronomical Society on 14 February 1896. On 27 October 1897 he was elected a member of the British Astronomical Association. He was also elected a Fellow of the Royal Society on 3 May 1906. In 1911 he won the Gold Medal of the Royal Astronomical Society. In 1909, he discovered 4358 Lynn, a 10-kilometer sized main-belt asteroid and member of the Eunomia. In 1910, for their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jet Propulsion Laboratory Development Ephemeris
Jet Propulsion Laboratory Development Ephemeris (abbreved JPL DE(number), or simply DE(number)) designates one of a series of mathematical models of the Solar System produced at the Jet Propulsion Laboratory in Pasadena, California, for use in spacecraft navigation and astronomy. The models consist of numeric representations of positions, velocities and accelerations of major Solar System bodies, tabulated at equally spaced intervals of time, covering a specified span of years. Barycentric rectangular coordinates of the Sun, eight major planets and Pluto, and geocentric coordinates of the Moon are tabulated. History There have been many versions of the JPL DE, from the 1960s through the present, in support of both robotic and crewed spacecraft missions. Available documentation is sketchy, but we know DE69 was announced in 1969 to be the third release of the JPL Ephemeris Tapes, and was a special purpose, short-duration ephemeris. The then-current JPL Export Ephemeris was DE19. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Ephemeris
A fundamental ephemeris of the Solar System is a model of the objects of the system in space, with all of their positions and motions accurately represented. It is intended to be a high-precision primary reference for prediction and observation of those positions and motions, and which provides a basis for further refinement of the model. It is generally not intended to cover the entire life of the Solar System; usually a short-duration time span, perhaps a few centuries, is represented to high accuracy. Some long ephemerides cover several millennia to medium accuracy. They are published by the Jet Propulsion Laboratory as Development Ephemeris. The latest releases include DE430 which covers planetary and lunar ephemeris from Dec 21, 1549 to Jan 25, 2650 with high precision and is intended for general use for modern time periods . DE431 was created to cover a longer time period Aug 15, -13200 to March 15, 17191 with slightly less precision for use with historic observations and far ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's Principia of 1687. The name "celestial mechanics" is more recent than that. Newton wrote that the field should be called "rational mechanics." The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term "celestial mechanics." Prior to Kepler there was little connection between exact, quantitative prediction of planetary positions, using geometrical or arithmetical techniques, and contemporary discussions of the physical causes of the planets' motion. Johannes Kepler Johannes Kepler (1571–1630) was the first to closely integrate the predictive geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Constant
The gravitational constant (also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant), denoted by the capital letter , is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor). The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately The modern notation of Newton's law involving was introduced in the 1890s by C. V. Boys. The first impl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary (astronomy), primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits). The true anomaly is usually denoted by the Greek letters or , or the Latin letter , and is usually restricted to the range 0–360° (0–2π). As shown in the image, the true anomaly is one of three angular parameters (''anomalies'') that defines a position along an orbit, the other two being the eccentric anomaly and the mean anomaly. Formulas From state vectors For elliptic orbits, the true anomaly can be calculated from orbital state vectors as: : \nu = \arccos ::(if then replace by ) where: * v is the orbital velocity vector of the orbiting body, * e is the eccentricity vector, * r is the orbital position vector (segment ''FP'' in the figure) of the orbiting bod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)