Glauber Dynamics on:
[Wikipedia]
[Google]
[Amazon]
In
 In the Ising model, we have say N
In the Ising model, we have say N
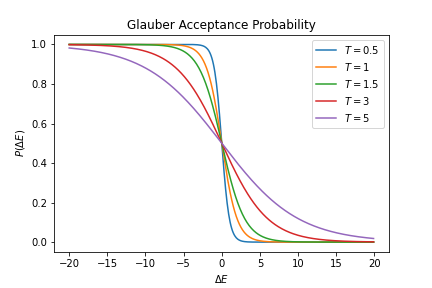
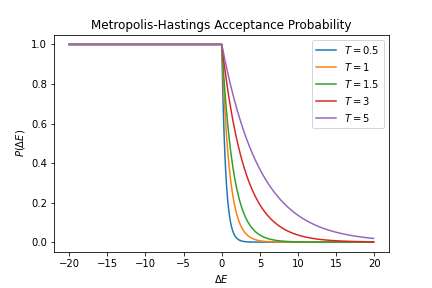 Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
In practice, the main difference between the
Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
In practice, the main difference between the
CRAN
statistical physics
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the Mathematics, mathematical tools for dealing with large populations ...
, Glauber dynamics is a way to simulate
A simulation is the imitation of the operation of a real-world process or system over time. Simulations require the use of Conceptual model, models; the model represents the key characteristics or behaviors of the selected system or proc ...
the Ising model
The Ising model () (or Lenz-Ising model or Ising-Lenz model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent ...
(a model of magnetism
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particles ...
) on a computer. It is a type of Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain ...
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specificat ...
.
The algorithm
 In the Ising model, we have say N
In the Ising model, we have say N particles
In the physical sciences, a particle (or corpuscule in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass.
They vary greatly in size or quantity, from s ...
that can spin up (+1) or down (-1). Say the particles are on a 2D grid. We label each with an x and y coordinate. Glauber's algorithm becomes:
# Choose a particle at random.
# Sum its four neighboring spins. .
# Compute the change in energy if the spin x, y were to flip. This is (see the Hamiltonian for the Ising model).
# Flip the spin with probability where T is the temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer.
Thermometers are calibrated in various temperature scales that historically have relied o ...
.
# Display the new grid. Repeat the above N times.
In Glauber algorithm, if the energy change in flipping a spin is zero, , then the spin would always gets flipped with probability .
Glauber V.S. Metropolis–Hastings algorithm
Metropolis–Hastings algorithm
In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. This seque ...
gives identical results as Glauber algorithm does, but it is faster. In the Metropolis algorithm, selecting a spin is deterministic. Usually, one may select the spins one by one following some order, for example “typewriter order”. In the Glauber dynamic, however, every spin has an equal chance of being chosen at each time step, regardless of being chosen before. The Metropolis acceptance criterion also includes the Boltzmann weight
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probabilit ...
, , but it always flips a spin in favor of lowering the energy, such that the spin-flip probability is:
. Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
In practice, the main difference between the
Although both of the acceptance probabilities approximate a step curve and they are almost indistinguishable at very low temperatures, they differ when temperature gets high. For an Ising model on a 2d lattice, the critical temperature is .
In practice, the main difference between the Metropolis–Hastings algorithm
In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. This seque ...
and with Glauber algorithm is in choosing the spins and how to flip them (step 4). However, at thermal equilibrium, these two algorithms should give identical results. In general, at equilibrium, any MCMC algorithm should produce the same distribution, as long as the algorithm satisfies ergodicity
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies th ...
and detailed balance The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes (collisions, or steps, or elementary reactions). It states that at equilibrium, each elementary process is in equilibrium with its reve ...
. In both algorithms, for any change in energy, , meaning that transition between the states of the system is always possible despite being very unlikely at some temperatures. So, the condition for ergodicity is satisfied for both of the algorithms. Detailed balance, which is a requirement of reversibility, states that if you observe the system for a long enough time, the system goes from state to with the same frequency as going from to . In equilibrium, the probability of observing the system at state A is given by the Boltzmann weight
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probabilit ...
, . So, the amount of time the system spends in low energy states is larger than in high energy states and there is more chance that the system is observed in states where it spends more time. Meaning that when the transition from to is energetically unfavorable, the system happens to be at more frequently, counterbalancing the lower intrinsic probability of transition. Therefore, both, Glauber and Metropolis–Hastings algorithms exhibit detailed balance.
History
The algorithm is named afterRoy J. Glauber
Roy Jay Glauber (September 1, 1925 – December 26, 2018) was an American theoretical physicist. He was the Mallinckrodt Professor of Physics at Harvard University and Adjunct Professor of Optical Sciences at the University of Arizona. Born in New ...
.
Software
* Simulation package IsingLenzMC provides simulation of Glauber Dynamics on 1D lattices with external fieldCRAN
Related pages
*Metropolis algorithm
A metropolis () is a large city or conurbation which is a significant economic, political, and cultural center for a country or region, and an important hub for regional or international connections, commerce, and communications.
A big c ...
* Ising model
The Ising model () (or Lenz-Ising model or Ising-Lenz model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent ...
* Monte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. Two examples of such algorithms are Karger–Stein algorithm and Monte Carlo algorithm for minimum Feedba ...
* Simulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It ...
References