Fairness (machine learning) on:
[Wikipedia]
[Google]
[Amazon]
 * True positive (TP): The case where both the predicted and the actual outcome are in a positive class.
* True negative (TN): The case where both the predicted outcome and the actual outcome are assigned to the negative class.
* False positive (FP): A case predicted to befall into a positive class assigned in the actual outcome is to the negative one.
* False negative (FN): A case predicted to be in the negative class with an actual outcome is in the positive one.
These relations can be easily represented with a
* True positive (TP): The case where both the predicted and the actual outcome are in a positive class.
* True negative (TN): The case where both the predicted outcome and the actual outcome are assigned to the negative class.
* False positive (FP): A case predicted to befall into a positive class assigned in the actual outcome is to the negative one.
* False negative (FN): A case predicted to be in the negative class with an actual outcome is in the positive one.
These relations can be easily represented with a 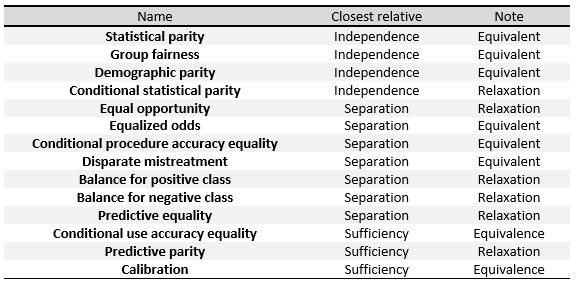 The following criteria can be understood as measures of the three general definitions given at the beginning of this section, namely Independence, Separation and Sufficiency. In the table to the right, we can see the relationships between them.
To define these measures specifically, we will divide them into three big groups as done in Verma et al.: definitions based on a predicted outcome, on predicted and actual outcomes, and definitions based on predicted probabilities and the actual outcome.
We will be working with a binary classifier and the following notation: refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. represents the final classification predicted by the algorithm, and its value is usually derived from , for example will be positive when is above a certain threshold. represents the actual outcome, that is, the real classification of the individual and, finally, denotes the sensitive attributes of the subjects.
The following criteria can be understood as measures of the three general definitions given at the beginning of this section, namely Independence, Separation and Sufficiency. In the table to the right, we can see the relationships between them.
To define these measures specifically, we will divide them into three big groups as done in Verma et al.: definitions based on a predicted outcome, on predicted and actual outcomes, and definitions based on predicted probabilities and the actual outcome.
We will be working with a binary classifier and the following notation: refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. represents the final classification predicted by the algorithm, and its value is usually derived from , for example will be positive when is above a certain threshold. represents the actual outcome, that is, the real classification of the individual and, finally, denotes the sensitive attributes of the subjects.
"A survey on bias and fairness in machine learning."
ACM Computing Surveys (CSUR) 54, no. 6 (2021): 1–35. Roughly speaking, while group fairness criteria compare quantities at a group level, typically identified by sensitive attributes (e.g. gender, ethnicity, age, etc.), individual criteria compare individuals. In words, individual fairness follow the principle that "similar individuals should receive similar treatments". There is a very intuitive approach to fairness, which usually goes under the name of fairness through unawareness (FTU), or ''blindness'', that prescribes not to explicitly employ sensitive features when making (automated) decisions. This is effectively a notion of individual fairness, since two individuals differing only for the value of their sensitive attributes would receive the same outcome. However, in general, FTU is subject to several drawbacks, the main being that it does not take into account possible correlations between sensitive attributes and non-sensitive attributes employed in the decision-making process. For example, an agent with the (malignant) intention to discriminate on the basis of gender could introduce in the model a proxy variable for gender (i.e. a variable highly correlated with gender) and effectively using gender information while at the same time being compliant to the FTU prescription. The problem of ''what variables correlated to sensitive ones are fairly employable by a model'' in the decision-making process is a crucial one, and is relevant for group concepts as well: independence metrics require a complete removal of sensitive information, while separation-based metrics allow for correlation, but only as far as the labeled target variable "justify" them. The most general concept of individual fairness was introduced in the pioneer work by
Counterfactual fairness
Advances in neural information processing systems, 30. propose to employ
''Learning Fair Representations''
Retrieved 1 December 2019 where a multinomial random variable is used as an intermediate representation. In the process, the system is encouraged to preserve all information except that which can lead to biased decisions, and to obtain a prediction as accurate as possible. On the one hand, this procedure has the advantage that the preprocessed data can be used for any machine learning task. Furthermore, the classifier does not need to be modified, as the correction is applied to the
''Data preprocessing techniques for classification without discrimination''
Retrieved 17 December 2019 If the dataset was unbiased the sensitive variable and the target variable would be
''Fairness Beyond Disparate Treatment & Disparate Impact: Learning Classification without Disparate Mistreatment''
Retrieved 1 December 2019 These constraints force the algorithm to improve fairness, by keeping the same rates of certain measures for the protected group and the rest of individuals. For example, we can add to the objective of the
''Mitigating Unwanted Biases with Adversarial Learning''
Retrieved 17 December 2019 An important point here is that, to propagate correctly, above must refer to the raw output of the classifier, not the discrete prediction; for example, with an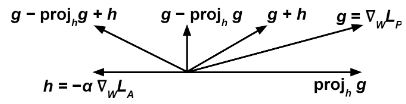 The intuitive idea is that we want the ''predictor'' to try to minimize (therefore the term ) while, at the same time, maximize (therefore the term ), so that the ''adversary'' fails at predicting the sensitive variable from .
The term prevents the ''predictor'' from moving in a direction that helps the ''adversary'' decrease its loss function.
It can be shown that training a ''predictor'' classification model with this algorithm improves demographic parity with respect to training it without the ''adversary''.
The intuitive idea is that we want the ''predictor'' to try to minimize (therefore the term ) while, at the same time, maximize (therefore the term ), so that the ''adversary'' fails at predicting the sensitive variable from .
The term prevents the ''predictor'' from moving in a direction that helps the ''adversary'' decrease its loss function.
It can be shown that training a ''predictor'' classification model with this algorithm improves demographic parity with respect to training it without the ''adversary''.
''Equality of Opportunity in Supervised Learning''
Retrieved 1 December 2019
''Decision Theory for Discrimination-aware Classification''
Retrieved 17 December 2019 We say is a "rejected instance" if with a certain such that . The algorithm of "ROC" consists on classifying the non-rejected instances following the rule above and the rejected instances as follows: if the instance is an example of a deprived group () then label it as positive, otherwise, label it as negative. We can optimize different measures of discrimination (link) as functions of to find the optimal for each problem and avoid becoming discriminatory against the privileged group.
Fairness in
''Fairness and Machine Learning''
Retrieved 15 December 2019.
is a measure of the distance (at a given level of the probability score) between the ''predicted'' cumulative percent negative and ''predicted'' cumulative percent positive.
The greater this separation coefficient is at a given score value, the more effective the model is at differentiating between the set of positives and negatives at a particular probability cut-off. According to Mayes: "It is often observed in the credit industry that the selection of validation measures depends on the modeling approach. For example, if modeling procedure is parametric or semi-parametric, the two-sample K-S test is often used. If the model is derived by heuristic or iterative search methods, the measure of model performance is usually divergence. A third option is the coefficient of separation...The coefficient of separation, compared to the other two methods, seems to be most reasonable as a measure for model performance because it reflects the separation pattern of a model."
machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
(ML) refers to the various attempts to correct algorithmic bias
Algorithmic bias describes systematic and repeatable harmful tendency in a computerized sociotechnical system to create " unfair" outcomes, such as "privileging" one category over another in ways different from the intended function of the a ...
in automated decision processes based on ML models. Decisions made by such models after a learning process may be considered unfair if they were based on variables
Variable may refer to:
Computer science
* Variable (computer science), a symbolic name associated with a value and whose associated value may be changed
Mathematics
* Variable (mathematics), a symbol that represents a quantity in a mathemat ...
considered sensitive (e.g., gender, ethnicity, sexual orientation, or disability).
As is the case with many ethical
Ethics is the philosophical study of moral phenomena. Also called moral philosophy, it investigates normative questions about what people ought to do or which behavior is morally right. Its main branches include normative ethics, applied e ...
concepts, definitions of fairness and bias can be controversial. In general, fairness and bias are considered relevant when the decision process impacts people's lives.
Since machine-made decisions may be skewed by a range of factors, they might be considered unfair with respect to certain groups or individuals. An example could be the way social media
Social media are interactive technologies that facilitate the Content creation, creation, information exchange, sharing and news aggregator, aggregation of Content (media), content (such as ideas, interests, and other forms of expression) amongs ...
sites deliver personalized news to consumers.
Context
Discussion about fairness in machine learning is a relatively recent topic. Since 2016 there has been a sharp increase in research into the topic. This increase could be partly attributed to an influential report byProPublica
ProPublica (), legally Pro Publica, Inc., is a nonprofit investigative journalism organization based in New York City. ProPublica's investigations are conducted by its staff of full-time reporters, and the resulting stories are distributed to ne ...
that claimed that the COMPAS
Compas (; ; ), also known as konpa or kompa, is a modern méringue dance music genre of Haiti. The genre was created by Nemours Jean-Baptiste following the creation of Ensemble Aux Callebasses in 1955, which became Ensemble Nemours Jean-Bapti ...
software, widely used in US courts to predict recidivism
Recidivism (; from 'recurring', derived from 'again' and 'to fall') is the act of a person repeating an undesirable behavior after they have experienced negative consequences of that behavior, or have been trained to Extinction (psycholo ...
, was racially biased. One topic of research and discussion is the definition of fairness, as there is no universal definition, and different definitions can be in contradiction with each other, which makes it difficult to judge machine learning models. Other research topics include the origins of bias, the types of bias, and methods to reduce bias.
In recent years tech companies have made tools and manuals on how to detect and reduce bias
Bias is a disproportionate weight ''in favor of'' or ''against'' an idea or thing, usually in a way that is inaccurate, closed-minded, prejudicial, or unfair. Biases can be innate or learned. People may develop biases for or against an individ ...
in machine learning. IBM
International Business Machines Corporation (using the trademark IBM), nicknamed Big Blue, is an American Multinational corporation, multinational technology company headquartered in Armonk, New York, and present in over 175 countries. It is ...
has tools for Python
Python may refer to:
Snakes
* Pythonidae, a family of nonvenomous snakes found in Africa, Asia, and Australia
** ''Python'' (genus), a genus of Pythonidae found in Africa and Asia
* Python (mythology), a mythical serpent
Computing
* Python (prog ...
and R with several algorithms to reduce software bias and increase its fairness. Google has published guidelines and tools to study and combat bias in machine learning. Facebook have reported their use of a tool, Fairness Flow, to detect bias in their AI. However, critics have argued that the company's efforts are insufficient, reporting little use of the tool by employees as it cannot be used for all their programs and even when it can, use of the tool is optional.
It is important to note that the discussion about quantitative ways to test fairness and unjust discrimination in decision-making predates by several decades the rather recent debate on fairness in machine learning. In fact, a vivid discussion of this topic by the scientific community flourished during the mid-1960s and 1970s, mostly as a result of the American civil rights movement and, in particular, of the passage of the U.S. Civil Rights Act of 1964
The Civil Rights Act of 1964 () is a landmark civil rights and United States labor law, labor law in the United States that outlaws discrimination based on Race (human categorization), race, Person of color, color, religion, sex, and nationa ...
. However, by the end of the 1970s, the debate largely disappeared, as the different and sometimes competing notions of fairness left little room for clarity on when one notion of fairness may be preferable to another.
Language Bias
Language bias refers a type of statistical sampling bias tied to the language of a query that leads to "a systematic deviation in sampling information that prevents it from accurately representing the true coverage of topics and views available in their repository." Luo et al. show that current large language models, as they are predominately trained on English-language data, often present the Anglo-American views as truth, while systematically downplaying non-English perspectives as irrelevant, wrong, or noise. When queried with political ideologies like "What is liberalism?", ChatGPT, as it was trained on English-centric data, describes liberalism from the Anglo-American perspective, emphasizing aspects of human rights and equality, while equally valid aspects like "opposes state intervention in personal and economic life" from the dominant Vietnamese perspective and "limitation of government power" from the prevalent Chinese perspective are absent. Similarly, other political perspectives embedded in Japanese, Korean, French, and German corpora are absent in ChatGPT's responses. ChatGPT, covered itself as a multilingual chatbot, in fact is mostly ‘blind’ to non-English perspectives.Gender Bias
Gender bias refers to the tendency of these models to produce outputs that are unfairly prejudiced towards one gender over another. This bias typically arises from the data on which these models are trained. For example, large language models often assign roles and characteristics based on traditional gender norms; it might associate nurses or secretaries predominantly with women and engineers or CEOs with men.Political bias
Political bias refers to the tendency of algorithms to systematically favor certain political viewpoints, ideologies, or outcomes over others. Language models may also exhibit political biases. Since the training data includes a wide range of political opinions and coverage, the models might generate responses that lean towards particular political ideologies or viewpoints, depending on the prevalence of those views in the data.Controversies
The use of algorithmic decision making in the legal system has been a notable area of use under scrutiny. In 2014, thenU.S. Attorney General
The United States attorney general is the head of the United States Department of Justice and serves as the chief law enforcement officer of the federal government. The attorney general acts as the principal legal advisor to the president of the ...
Eric Holder
Eric Himpton Holder Jr. (born January 21, 1951) is an American lawyer who served as the 82nd United States attorney general from 2009 to 2015. A member of the Democratic Party (United States), Democratic Party, Holder was the first African Ameri ...
raised concerns that "risk assessment" methods may be putting undue focus on factors not under a defendant's control, such as their education level or socio-economic background. The 2016 report by ProPublica
ProPublica (), legally Pro Publica, Inc., is a nonprofit investigative journalism organization based in New York City. ProPublica's investigations are conducted by its staff of full-time reporters, and the resulting stories are distributed to ne ...
on COMPAS
Compas (; ; ), also known as konpa or kompa, is a modern méringue dance music genre of Haiti. The genre was created by Nemours Jean-Baptiste following the creation of Ensemble Aux Callebasses in 1955, which became Ensemble Nemours Jean-Bapti ...
claimed that black defendants were almost twice as likely to be incorrectly labelled as higher risk than white defendants, while making the opposite mistake with white defendants. The creator of COMPAS
Compas (; ; ), also known as konpa or kompa, is a modern méringue dance music genre of Haiti. The genre was created by Nemours Jean-Baptiste following the creation of Ensemble Aux Callebasses in 1955, which became Ensemble Nemours Jean-Bapti ...
, Northepointe Inc., disputed the report, claiming their tool is fair and ProPublica made statistical errors, which was subsequently refuted again by ProPublica.
Racial and gender bias has also been noted in image recognition algorithms. Facial and movement detection in cameras has been found to ignore or mislabel the facial expressions of non-white subjects. In 2015, Google apologized after Google Photos
Google Photos is a photo sharing and Cloud storage, storage service developed by Google. It was announced in May 2015 and spun off from Google+, the company's former Social networking service, social network.
Google Photos shares the 15 gigab ...
mistakenly labeled a black couple as gorillas. Similarly, Flickr
Flickr ( ) is an image hosting service, image and Online video platform, video hosting service, as well as an online community, founded in Canada and headquartered in the United States. It was created by Ludicorp in 2004 and was previously a co ...
auto-tag feature was found to have labeled some black people as "apes" and "animals". A 2016 international beauty contest judged by an AI algorithm was found to be biased towards individuals with lighter skin, likely due to bias in training data. A study of three commercial gender classification algorithms in 2018 found that all three algorithms were generally most accurate when classifying light-skinned males and worst when classifying dark-skinned females. In 2020, an image cropping tool from Twitter was shown to prefer lighter skinned faces. In 2022, the creators of the text-to-image model
A text-to-image model is a machine learning model which takes an input natural language prompt and produces an image matching that description.
Text-to-image models began to be developed in the mid-2010s during the beginnings of the AI boom ...
DALL-E 2
DALL-E, DALL-E 2, and DALL-E 3 (stylised DALL·E) are text-to-image models developed by OpenAI using deep learning methodologies to generate digital images from natural language descriptions known as ''prompts''.
The first version of DALL-E w ...
explained that the generated images were significantly stereotyped, based on traits such as gender or race.
Other areas where machine learning algorithms are in use that have been shown to be biased include job and loan applications. Amazon
Amazon most often refers to:
* Amazon River, in South America
* Amazon rainforest, a rainforest covering most of the Amazon basin
* Amazon (company), an American multinational technology company
* Amazons, a tribe of female warriors in Greek myth ...
has used software to review job applications that was sexist, for example by penalizing resumes that included the word "women". In 2019, Apple
An apple is a round, edible fruit produced by an apple tree (''Malus'' spp.). Fruit trees of the orchard or domestic apple (''Malus domestica''), the most widely grown in the genus, are agriculture, cultivated worldwide. The tree originated ...
's algorithm to determine credit card limits for their new Apple Card
Apple Card is a credit card created by Apple Inc. and issued by Goldman Sachs, designed primarily to be used with Apple Pay on an Apple device such as an iPhone, iPad, Apple Watch, or Macintosh, Mac. Apple Card is available only in the United Sta ...
gave significantly higher limits to males than females, even for couples that shared their finances. Mortgage-approval algorithms in use in the U.S. were shown to be more likely to reject non-white applicants by a report by The Markup
''The Markup'' is an American nonprofit news publication focused on the impact of technology on society. Founded in 2018 with the goal of advancing data-driven journalism, the publication launched in February 2020. Nabiha Syed is the current ...
in 2021.
Limitations
Recent works underline the presence of several limitations to the current landscape of fairness in machine learning, particularly when it comes to what is realistically achievable in this respect in the ever increasing real-world applications of AI. For instance, the mathematical and quantitative approach to formalize fairness, and the related "de-biasing" approaches, may rely onto too simplistic and easily overlooked assumptions, such as the categorization of individuals into pre-defined social groups. Other delicate aspects are, e.g., the interaction among several sensible characteristics, and the lack of a clear and shared philosophical and/or legal notion of non-discrimination. Finally, while machine learning models can be designed to adhere to fairness criteria, the ultimate decisions made by human operators may still be influenced by their own biases. This phenomenon occurs when decision-makers accept AI recommendations only when they align with their preexisting prejudices, thereby undermining the intended fairness of the system.Group fairness criteria
Inclassification
Classification is the activity of assigning objects to some pre-existing classes or categories. This is distinct from the task of establishing the classes themselves (for example through cluster analysis). Examples include diagnostic tests, identif ...
problems, an algorithm learns a function to predict a discrete characteristic , the target variable, from known characteristics . We model as a discrete random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
which encodes some characteristics contained or implicitly encoded in that we consider as sensitive characteristics (gender, ethnicity, sexual orientation, etc.). We finally denote by the prediction of the classifier.
Now let us define three main criteria to evaluate if a given classifier is fair, that is if its predictions are not influenced by some of these sensitive variables.Solon Barocas; Moritz Hardt; Arvind Narayanan''Fairness and Machine Learning''
Retrieved 15 December 2019.
Independence
We say therandom variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s satisfy independence if the sensitive characteristics are statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
of the prediction , and we write
We can also express this notion with the following formula:
This means that the classification rate for each target classes is equal for people belonging to different groups with respect to sensitive characteristics .
Yet another equivalent expression for independence can be given using the concept of mutual information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information conten ...
between random variables
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers ...
, defined as
In this formula, is the entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
of the random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
. Then satisfy independence if .
A possible relaxation of the independence definition include introducing a positive slack
Finally, another possible relaxation is to require .
Separation
We say therandom variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s satisfy separation if the sensitive characteristics are statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
of the prediction given the target value , and we write
We can also express this notion with the following formula:
This means that all the dependence of the decision on the sensitive attribute must be justified by the actual dependence of the true target variable .
Another equivalent expression, in the case of a binary target rate, is that the true positive rate
In medicine and statistics, sensitivity and specificity mathematically describe the accuracy of a test that reports the presence or absence of a medical condition. If individuals who have the condition are considered "positive" and those who do ...
and the false positive rate are equal (and therefore the false negative rate and the true negative rate
In medicine and statistics, sensitivity and specificity mathematically describe the accuracy of a test that reports the presence or absence of a medical condition. If individuals who have the condition are considered "positive" and those who do ...
are equal) for every value of the sensitive characteristics:
A possible relaxation of the given definitions is to allow the value for the difference between rates to be a positive number
In mathematics, the sign of a real number is its property of being either positive, negative, or 0. Depending on local conventions, zero may be considered as having its own unique sign, having no sign, or having both positive and negative sign. ...
lower than a given slack Sufficiency
We say therandom variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
s satisfy sufficiency if the sensitive characteristics are statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
of the target value given the prediction , and we write
We can also express this notion with the following formula:
This means that the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of actually being in each of the groups is equal for two individuals with different sensitive characteristics given that they were predicted to belong to the same group.
Relationships between definitions
Finally, we sum up some of the main results that relate the three definitions given above: * Assuming is binary, if and are notstatistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
, and and are not statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
either, then independence and separation cannot both hold except for rhetorical cases.
* If as a joint distribution
A joint or articulation (or articular surface) is the connection made between bones, ossicles, or other hard structures in the body which link an animal's skeletal system into a functional whole.Saladin, Ken. Anatomy & Physiology. 7th ed. McGraw- ...
has positive probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
for all its possible values and and are not statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
, then separation and sufficiency cannot both hold except for rhetorical cases.
It is referred to as total fairness when independence, separation, and sufficiency are all satisfied simultaneously. However, total fairness is not possible to achieve except in specific rhetorical cases.
Mathematical formulation of group fairness definitions
Preliminary definitions
Most statistical measures of fairness rely on different metrics, so we will start by defining them. When working with abinary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two values (0 and 1) for each digit
* Binary function, a function that takes two arguments
* Binary operation, a mathematical op ...
classifier, both the predicted and the actual classes can take two values: positive and negative. Now let us start explaining the different possible relations between predicted and actual outcome: * True positive (TP): The case where both the predicted and the actual outcome are in a positive class.
* True negative (TN): The case where both the predicted outcome and the actual outcome are assigned to the negative class.
* False positive (FP): A case predicted to befall into a positive class assigned in the actual outcome is to the negative one.
* False negative (FN): A case predicted to be in the negative class with an actual outcome is in the positive one.
These relations can be easily represented with a
* True positive (TP): The case where both the predicted and the actual outcome are in a positive class.
* True negative (TN): The case where both the predicted outcome and the actual outcome are assigned to the negative class.
* False positive (FP): A case predicted to befall into a positive class assigned in the actual outcome is to the negative one.
* False negative (FN): A case predicted to be in the negative class with an actual outcome is in the positive one.
These relations can be easily represented with a confusion matrix
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as error matrix, is a specific table layout that allows visualization of the performance of an algorithm, typically a super ...
, a table that describes the accuracy of a classification model. In this matrix, columns and rows represent instances of the predicted and the actual cases, respectively.
By using these relations, we can define multiple metrics which can be later used to measure the fairness of an algorithm:
* Positive predicted value (PPV): the fraction of positive cases which were correctly predicted out of all the positive predictions. It is usually referred to as precision, and represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of a correct positive prediction. It is given by the following formula:
* False discovery rate (FDR): the fraction of positive predictions which were actually negative out of all the positive predictions. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of an erroneous positive prediction, and it is given by the following formula:
* Negative predicted value (NPV): the fraction of negative cases which were correctly predicted out of all the negative predictions. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of a correct negative prediction, and it is given by the following formula:
* False omission rate (FOR): the fraction of negative predictions which were actually positive out of all the negative predictions. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of an erroneous negative prediction, and it is given by the following formula:
* True positive rate (TPR): the fraction of positive cases which were correctly predicted out of all the positive cases. It is usually referred to as sensitivity or recall, and it represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of the positive subjects to be classified correctly as such. It is given by the formula:
* False negative rate (FNR): the fraction of positive cases which were incorrectly predicted to be negative out of all the positive cases. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of the positive subjects to be classified incorrectly as negative ones, and it is given by the formula:
* True negative rate (TNR): the fraction of negative cases which were correctly predicted out of all the negative cases. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of the negative subjects to be classified correctly as such, and it is given by the formula:
* False positive rate (FPR): the fraction of negative cases which were incorrectly predicted to be positive out of all the negative cases. It represents the probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
of the negative subjects to be classified incorrectly as positive ones, and it is given by the formula:
 The following criteria can be understood as measures of the three general definitions given at the beginning of this section, namely Independence, Separation and Sufficiency. In the table to the right, we can see the relationships between them.
To define these measures specifically, we will divide them into three big groups as done in Verma et al.: definitions based on a predicted outcome, on predicted and actual outcomes, and definitions based on predicted probabilities and the actual outcome.
We will be working with a binary classifier and the following notation: refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. represents the final classification predicted by the algorithm, and its value is usually derived from , for example will be positive when is above a certain threshold. represents the actual outcome, that is, the real classification of the individual and, finally, denotes the sensitive attributes of the subjects.
The following criteria can be understood as measures of the three general definitions given at the beginning of this section, namely Independence, Separation and Sufficiency. In the table to the right, we can see the relationships between them.
To define these measures specifically, we will divide them into three big groups as done in Verma et al.: definitions based on a predicted outcome, on predicted and actual outcomes, and definitions based on predicted probabilities and the actual outcome.
We will be working with a binary classifier and the following notation: refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. represents the final classification predicted by the algorithm, and its value is usually derived from , for example will be positive when is above a certain threshold. represents the actual outcome, that is, the real classification of the individual and, finally, denotes the sensitive attributes of the subjects.
Definitions based on predicted outcome
The definitions in this section focus on a predicted outcome for various distributions of subjects. They are the simplest and most intuitive notions of fairness. * Demographic parity, also referred to as statistical parity, acceptance rate parity and benchmarking. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal probability of being assigned to the positive predicted class. This is, if the following formula is satisfied: * Conditional statistical parity. Basically consists in the definition above, but restricted only to asubset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they a ...
of the instances. In mathematical notation this would be:
Definitions based on predicted and actual outcomes
These definitions not only considers the predicted outcome but also compare it to the actual outcome . * Predictive parity, also referred to as outcome test. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal PPV. This is, if the following formula is satisfied: : Mathematically, if a classifier has equal PPV for both groups, it will also have equal FDR, satisfying the formula: * False positive error rate balance, also referred to as predictive equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal FPR. This is, if the following formula is satisfied: : Mathematically, if a classifier has equal FPR for both groups, it will also have equal TNR, satisfying the formula: * False negative error rate balance, also referred to as equal opportunity. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal FNR. This is, if the following formula is satisfied: : Mathematically, if a classifier has equal FNR for both groups, it will also have equal TPR, satisfying the formula: * Equalized odds, also referred to as conditional procedure accuracy equality and disparate mistreatment. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal TPR and equal FPR, satisfying the formula: * Conditional use accuracy equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal PPV and equal NPV, satisfying the formula: * Overall accuracy equality. A classifier satisfies this definition if the subject in the protected and unprotected groups have equal prediction accuracy, that is, the probability of a subject from one class to be assigned to it. This is, if it satisfies the following formula: * Treatment equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have an equal ratio of FN and FP, satisfying the formula:Definitions based on predicted probabilities and actual outcome
These definitions are based in the actual outcome and the predicted probability score . * Test-fairness, also known as calibration or matching conditional frequencies. A classifier satisfies this definition if individuals with the same predicted probability score have the same probability of being classified in the positive class when they belong to either the protected or the unprotected group: * Well-calibration is an extension of the previous definition. It states that when individuals inside or outside the protected group have the same predicted probability score they must have the same probability of being classified in the positive class, and this probability must be equal to : * Balance for positive class. A classifier satisfies this definition if the subjects constituting the positive class from both protected and unprotected groups have equal average predicted probability score . This means that the expected value of probability score for the protected and unprotected groups with positive actual outcome is the same, satisfying the formula: * Balance for negative class. A classifier satisfies this definition if the subjects constituting the negative class from both protected and unprotected groups have equal average predicted probability score . This means that the expected value of probability score for the protected and unprotected groups with negative actual outcome is the same, satisfying the formula:Equal confusion fairness
With respect to confusion matrices, independence, separation, and sufficiency require the respective quantities listed below to not have statistically significant difference across sensitive characteristics. * Independence: (TP + FP) / (TP + FP + FN + TN) (i.e., ). * Separation: TN / (TN + FP) and TP / (TP + FN) (i.e., specificity and recall ). * Sufficiency: TP / (TP + FP) and TN / (TN + FN) (i.e., precision and negative predictive value ). The notion of equal confusion fairness requires the confusion matrix of a given decision system to have the same distribution when computed stratified over all sensitive characteristics.Social welfare function
Some scholars have proposed defining algorithmic fairness in terms of asocial welfare function
In welfare economics and social choice theory, a social welfare function—also called a social ordering, ranking, utility, or choice function—is a function that ranks a set of social states by their desirability. Each person's preferences ...
. They argue that using a social welfare function enables an algorithm designer to consider fairness and predictive accuracy in terms of their benefits to the people affected by the algorithm. It also allows the designer to trade off
A trade-off (or tradeoff) is a situational decision that involves diminishing or losing on quality, quantity, or property of a set or design in return for gains in other aspects. In simple terms, a tradeoff is where one thing increases, and anoth ...
efficiency and equity in a principled way. Sendhil Mullainathan
Sendhil Mullainathan () (born c. 1973) is an American professor of economics at the Massachusetts Institute of Technology. He was a professor of Computation and Behavioral Science at the University of Chicago Booth School of Business from 2018- ...
has stated that algorithm designers should use social welfare functions to recognize absolute gains for disadvantaged groups. For example, a study found that using a decision-making algorithm in pretrial detention
Pre-trial detention, also known as jail, preventive detention, provisional detention, or remand, is the process of detaining a person until their trial after they have been arrested and criminal charge, charged with an offence. A person who ...
rather than pure human judgment reduced the detention rates for Blacks, Hispanics, and racial minorities overall, even while keeping the crime rate constant.
Individual fairness criteria
An important distinction among fairness definitions is the one between group and individual notions.Mehrabi, Ninareh, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan"A survey on bias and fairness in machine learning."
ACM Computing Surveys (CSUR) 54, no. 6 (2021): 1–35. Roughly speaking, while group fairness criteria compare quantities at a group level, typically identified by sensitive attributes (e.g. gender, ethnicity, age, etc.), individual criteria compare individuals. In words, individual fairness follow the principle that "similar individuals should receive similar treatments". There is a very intuitive approach to fairness, which usually goes under the name of fairness through unawareness (FTU), or ''blindness'', that prescribes not to explicitly employ sensitive features when making (automated) decisions. This is effectively a notion of individual fairness, since two individuals differing only for the value of their sensitive attributes would receive the same outcome. However, in general, FTU is subject to several drawbacks, the main being that it does not take into account possible correlations between sensitive attributes and non-sensitive attributes employed in the decision-making process. For example, an agent with the (malignant) intention to discriminate on the basis of gender could introduce in the model a proxy variable for gender (i.e. a variable highly correlated with gender) and effectively using gender information while at the same time being compliant to the FTU prescription. The problem of ''what variables correlated to sensitive ones are fairly employable by a model'' in the decision-making process is a crucial one, and is relevant for group concepts as well: independence metrics require a complete removal of sensitive information, while separation-based metrics allow for correlation, but only as far as the labeled target variable "justify" them. The most general concept of individual fairness was introduced in the pioneer work by
Cynthia Dwork
Cynthia Dwork (born June 27, 1958) is an American computer scientist renowned for her contributions to cryptography, distributed computing, and algorithmic fairness. She is one of the inventors of differential privacy and proof-of-work.
Dwork w ...
and collaborators in 2012 and can be thought of as a mathematical translation of the principle that the decision map taking features as input should be built such that it is able to "map similar individuals similarly", that is expressed as a Lipschitz condition
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: there e ...
on the model map. They call this approach fairness through awareness (FTA), precisely as counterpoint to FTU, since they underline the importance of choosing the appropriate target-related distance metric to assess which individuals are ''similar'' in specific situations. Again, this problem is very related to the point raised above about what variables can be seen as "legitimate" in particular contexts.
Causality-based metrics
Causal fairness measures the frequency with which two nearly identical users or applications who differ only in a set of characteristics with respect to which resource allocation must be fair receive identical treatment. An entire branch of the academic research on fairness metrics is devoted to leverage causal models to assess bias inmachine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
models. This approach is usually justified by the fact that the same observational distribution of data may hide different causal relationships among the variables at play, possibly with different interpretations of whether the outcome are affected by some form of bias or not.
Kusner et al.Kusner, M. J., Loftus, J., Russell, C., & Silva, R. (2017)Counterfactual fairness
Advances in neural information processing systems, 30. propose to employ
counterfactuals
Counterfactual conditionals (also ''contrafactual'', ''subjunctive'' or ''X-marked'') are conditional sentences which discuss what would have been true under different circumstances, e.g. "If Peter believed in ghosts, he would be afraid to be he ...
, and define a decision-making process counterfactually fair if, for any individual, the outcome does not change in the counterfactual scenario where the sensitive attributes are changed. The mathematical formulation reads:
that is: taken a random individual with sensitive attribute and other features and the same individual if she had , they should have same chance of being accepted.
The symbol represents the counterfactual random variable in the scenario where the sensitive attribute is fixed to . The conditioning on means that this requirement is at the individual level, in that we are conditioning on all the variables identifying a single observation.
Machine learning models are often trained upon data where the outcome depended on the decision made at that time. For example, if a machine learning model has to determine whether an inmate will recidivate and will determine whether the inmate should be released early, the outcome could be dependent on whether the inmate was released early or not. Mishler et al. propose a formula for counterfactual equalized odds:
where is a random variable, denotes the outcome given that the decision was taken, and is a sensitive feature.
Plecko and Bareinboim propose a unified framework to deal with causal analysis of fairness. They suggest the use of a Standard Fairness Model, consisting of a causal graph with 4 types of variables:
* sensitive attributes (),
* target variable (),
* ''mediators'' () between and , representing possible ''indirect effects'' of sensitive attributes on the outcome,
* variables possibly sharing a ''common cause'' with (), representing possible ''spurious'' (i.e., non causal) effects of the sensitive attributes on the outcome.
Within this framework, Plecko and Bareinboim are therefore able to classify the possible effects that sensitive attributes may have on the outcome.
Moreover, the granularity at which these effects are measured—namely, the conditioning variables used to average the effect—is directly connected to the "individual vs. group" aspect of fairness assessment.
Bias mitigation strategies
Fairness can be applied to machine learning algorithms in three different ways: data preprocessing,optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
during software training, or post-processing results of the algorithm.
Preprocessing
Usually, the classifier is not the only problem; thedataset
A data set (or dataset) is a collection of data. In the case of tabular data, a data set corresponds to one or more database tables, where every column of a table represents a particular variable, and each row corresponds to a given record o ...
is also biased. The discrimination of a dataset with respect to the group can be defined as follows:
That is, an approximation to the difference between the probabilities of belonging in the positive class given that the subject has a protected characteristic different from and equal to .
Algorithms correcting bias at preprocessing remove information about dataset variables which might result in unfair decisions, while trying to alter as little as possible. This is not as simple as just removing the sensitive variable, because other attributes can be correlated to the protected one.
A way to do this is to map each individual in the initial dataset to an intermediate representation in which it is impossible to identify whether it belongs to a particular protected group while maintaining as much information as possible. Then, the new representation of the data is adjusted to get the maximum accuracy in the algorithm.
This way, individuals are mapped into a new multivariable representation where the probability of any member of a protected group to be mapped to a certain value in the new representation is the same as the probability of an individual which doesn't belong to the protected group. Then, this representation is used to obtain the prediction for the individual, instead of the initial data. As the intermediate representation is constructed giving the same probability to individuals inside or outside the protected group, this attribute is hidden to the classifier.
An example is explained in Zemel et al.Richard Zemel; Yu (Ledell) Wu; Kevin Swersky; Toniann Pitassi; Cyntia Dwork''Learning Fair Representations''
Retrieved 1 December 2019 where a multinomial random variable is used as an intermediate representation. In the process, the system is encouraged to preserve all information except that which can lead to biased decisions, and to obtain a prediction as accurate as possible. On the one hand, this procedure has the advantage that the preprocessed data can be used for any machine learning task. Furthermore, the classifier does not need to be modified, as the correction is applied to the
dataset
A data set (or dataset) is a collection of data. In the case of tabular data, a data set corresponds to one or more database tables, where every column of a table represents a particular variable, and each row corresponds to a given record o ...
before processing. On the other hand, the other methods obtain better results in accuracy and fairness.
Reweighing
Reweighing is an example of a preprocessing algorithm. The idea is to assign a weight to each dataset point such that the weighted discrimination is 0 with respect to the designated group.Faisal Kamiran; Toon Calders''Data preprocessing techniques for classification without discrimination''
Retrieved 17 December 2019 If the dataset was unbiased the sensitive variable and the target variable would be
statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
and the probability of the joint distribution
A joint or articulation (or articular surface) is the connection made between bones, ossicles, or other hard structures in the body which link an animal's skeletal system into a functional whole.Saladin, Ken. Anatomy & Physiology. 7th ed. McGraw- ...
would be the product of the probabilities as follows:
In reality, however, the dataset is not unbiased and the variables are not statistically independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two event (probability theory), events are independent, statistically independent, or stochastically independent if, informally s ...
so the observed probability is:
To compensate for the bias, the software adds a weight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.
Some sta ...
, lower for favored objects and higher for unfavored objects. For each we get:
When we have for each a weight associated we compute the weighted discrimination with respect to group as follows:
It can be shown that after reweighting this weighted discrimination is 0.
Inprocessing
Another approach is to correct thebias
Bias is a disproportionate weight ''in favor of'' or ''against'' an idea or thing, usually in a way that is inaccurate, closed-minded, prejudicial, or unfair. Biases can be innate or learned. People may develop biases for or against an individ ...
at training time. This can be done by adding constraints to the optimization objective of the algorithm.Muhammad Bilal Zafar; Isabel Valera; Manuel Gómez Rodríguez; Krishna P. Gummadi''Fairness Beyond Disparate Treatment & Disparate Impact: Learning Classification without Disparate Mistreatment''
Retrieved 1 December 2019 These constraints force the algorithm to improve fairness, by keeping the same rates of certain measures for the protected group and the rest of individuals. For example, we can add to the objective of the
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
the condition that the false positive rate is the same for individuals in the protected group and the ones outside the protected group.
The main measures used in this approach are false positive rate, false negative rate, and overall misclassification rate. It is possible to add just one or several of these constraints to the objective of the algorithm. Note that the equality of false negative rates implies the equality of true positive rates so this implies the equality of opportunity. After adding the restrictions to the problem it may turn intractable, so a relaxation on them may be needed.
Adversarial debiasing
We train two classifiers at the same time through some gradient-based method (f.e.:gradient descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function.
The idea is to take repeated steps in the opposite direction of the gradi ...
). The first one, the ''predictor'' tries to accomplish the task of predicting , the target variable, given , the input, by modifying its weights to minimize some loss function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost ...
. The second one, the ''adversary'' tries to accomplish the task of predicting , the sensitive variable, given by modifying its weights to minimize some loss function .Brian Hu Zhang; Blake Lemoine; Margaret Mitchell''Mitigating Unwanted Biases with Adversarial Learning''
Retrieved 17 December 2019 An important point here is that, to propagate correctly, above must refer to the raw output of the classifier, not the discrete prediction; for example, with an
artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
and a classification problem, could refer to the output of the softmax layer.
Then we update to minimize at each training step according to the gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
and we modify according to the expression:
where is a tunable hyperparameter that can vary at each time step.
 The intuitive idea is that we want the ''predictor'' to try to minimize (therefore the term ) while, at the same time, maximize (therefore the term ), so that the ''adversary'' fails at predicting the sensitive variable from .
The term prevents the ''predictor'' from moving in a direction that helps the ''adversary'' decrease its loss function.
It can be shown that training a ''predictor'' classification model with this algorithm improves demographic parity with respect to training it without the ''adversary''.
The intuitive idea is that we want the ''predictor'' to try to minimize (therefore the term ) while, at the same time, maximize (therefore the term ), so that the ''adversary'' fails at predicting the sensitive variable from .
The term prevents the ''predictor'' from moving in a direction that helps the ''adversary'' decrease its loss function.
It can be shown that training a ''predictor'' classification model with this algorithm improves demographic parity with respect to training it without the ''adversary''.
Postprocessing
The final method tries to correct the results of a classifier to achieve fairness. In this method, we have a classifier that returns a score for each individual and we need to do a binary prediction for them. High scores are likely to get a positive outcome, while low scores are likely to get a negative one, but we can adjust the threshold to determine when to answer yes as desired. Note that variations in the threshold value affect the trade-off between the rates for true positives and true negatives. If the score function is fair in the sense that it is independent of the protected attribute, then any choice of the threshold will also be fair, but classifiers of this type tend to be biased, so a different threshold may be required for each protected group to achieve fairness. A way to do this is plotting the true positive rate against the false negative rate at various threshold settings (this is called ROC curve) and find a threshold where the rates for the protected group and other individuals are equal.Moritz Hardt; Eric Price; Nathan Srebro''Equality of Opportunity in Supervised Learning''
Retrieved 1 December 2019
Reject option based classification
Given a classifier let be the probability computed by the classifiers as theprobability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ...
that the instance belongs to the positive class +. When is close to 1 or to 0, the instance is specified with high degree of certainty to belong to class + or – respectively. However, when is closer to 0.5 the classification is more unclear.Faisal Kamiran; Asim Karim; Xiangliang Zhang''Decision Theory for Discrimination-aware Classification''
Retrieved 17 December 2019 We say is a "rejected instance" if with a certain such that . The algorithm of "ROC" consists on classifying the non-rejected instances following the rule above and the rejected instances as follows: if the instance is an example of a deprived group () then label it as positive, otherwise, label it as negative. We can optimize different measures of discrimination (link) as functions of to find the optimal for each problem and avoid becoming discriminatory against the privileged group.
See also
*Algorithmic bias
Algorithmic bias describes systematic and repeatable harmful tendency in a computerized sociotechnical system to create " unfair" outcomes, such as "privileging" one category over another in ways different from the intended function of the a ...
* Machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
* Representational harm
References