|
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the suffix, and ''k'' the prefix). The Bernoulli distribution models the outcome of a si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergence Of Multinomial Distribution To The Gaussian Distribution
Convergence may refer to: Arts and media Literature *''Convergence'' (book series), edited by Ruth Nanda Anshen * "Convergence" (comics), two separate story lines published by DC Comics: **A four-part crossover storyline that united the four Weirdoverse titles in 1997 **A 2015 crossover storyline spanning the DC Comics Multiverse * ''Convergence'' (journal), an academic journal that covers the fields of communications and media * ''Convergence'' (novel), by Charles Sheffield * ''Convergence'' (Cherryh novel), by C. J. Cherryh Music * ''Convergence'' (Front Line Assembly album), 1988 * ''Convergence'' (David Arkenstone and David Lanz album), 1996 * ''Convergence'' (Dave Douglas album), 1999 * ''Convergence'' (Warren Wolf album), 2016 Other media * ''Convergence'' (Pollock), a 1952 oil painting by Jackson Pollock * ''Convergence'' (2015 film), an American horror-thriller film * ''Convergence'' (2019 film), a British drama film *''Convergence'', a 2021 Netflix film by Orlando von ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the \chi^2-distribution with k Degrees of freedom (statistics), degrees of freedom is the distribution of a sum of the squares of k Independence (probability theory), independent standard normal random variables. The chi-squared distribution \chi^2_k is a special case of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim \chi^2_k then X \sim \text(\alpha=\frac, \theta=2) (where \alpha is the shape parameter and \theta the scale parameter of the gamma distribution) and X \sim \text_1(1,k) . The scaled chi-squared distribution s^2 \chi^2_k is a reparametrization of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim s^2 \chi^2_k then X \sim \text(\alpha=\frac, \theta=2 s^2) and X \sim \text_1(s^2,k) . The chi-squared distribution is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in constru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Converges In Distribution
In probability theory, there exist several different notions of convergence of sequences of random variables, including ''convergence in probability'', ''convergence in distribution'', and ''almost sure convergence''. The different notions of convergence capture different properties about the sequence, with some notions of convergence being stronger than others. For example, convergence in distribution tells us about the limit distribution of a sequence of random variables. This is a weaker notion than convergence in probability, which tells us about the value a random variable will take, rather than just the distribution. The concept is important in probability theory, and its applications to statistics and stochastic processes. The same concepts are known in more general mathematics as stochastic convergence and they formalize the idea that certain properties of a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behavior that i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sanov's Theorem
In mathematics and information theory, Sanov's theorem gives a bound on the probability of observing an atypical sequence of samples from a given probability distribution. In the language of large deviations theory, Sanov's theorem identifies the rate function for large deviations of the empirical measure of a sequence of i.i.d. random variables. Let ''A'' be a set of probability distributions over an alphabet ''X'', and let ''q'' be an arbitrary distribution over ''X'' (where ''q'' may or may not be in ''A''). Suppose we draw ''n'' i.i.d. samples from ''q'', represented by the vector x^n = (x_1, x_2, \ldots, x_n). Then, we have the following bound on the probability that the empirical measure \hat_ of the samples falls within the set ''A'': :q^n(\hat_\in A) \le (n+1)^ 2^, where * q^n is the joint probability distribution on X^n, and * p^* is the information projection of ''q'' onto ''A''. * D_(P \, Q), the KL divergence, is given by: D_(P \, Q) = \sum_ P(x) \log \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
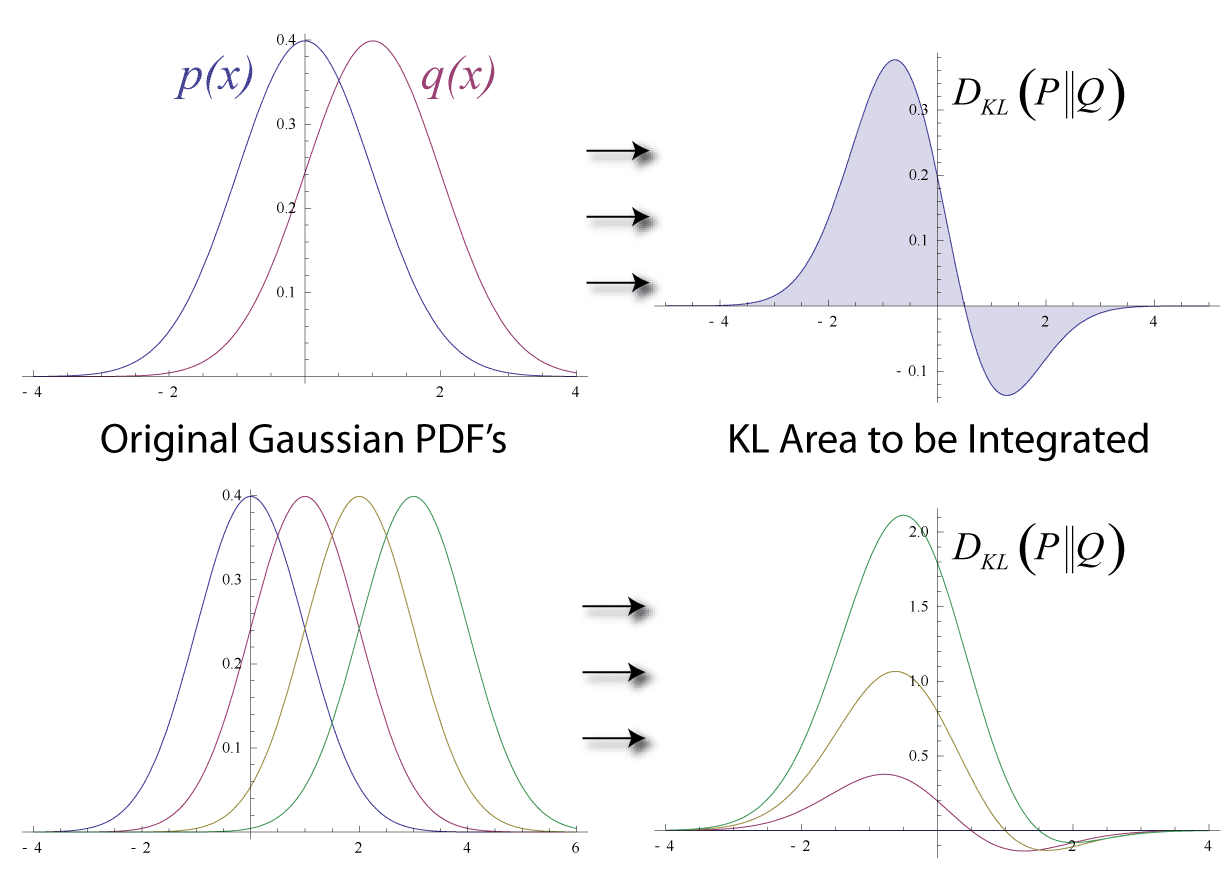
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling's Formula
In mathematics, Stirling's approximation (or Stirling's formula) is an Asymptotic analysis, asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling (mathematician), James Stirling, though a related but less precise result was first stated by Abraham de Moivre. One way of stating the approximation involves the logarithm of the factorial: \ln(n!) = n\ln n - n +O(\ln n), where the big O notation means that, for all sufficiently large values of n, the difference between \ln(n!) and n\ln n-n will be at most proportional to the logarithm of n. In computer science applications such as the Comparison sort#Number of comparisons required to sort a list, worst-case lower bound for comparison sorting, it is convenient to instead use the binary logarithm, giving the equivalent form \log_2 (n!) = n\log_2 n - n\log_2 e +O(\log_2 n). The error term in either base can be expressed more precisely as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. For example, * a 0-dimensional simplex is a point, * a 1-dimensional simplex is a line segment, * a 2-dimensional simplex is a triangle, * a 3-dimensional simplex is a tetrahedron, and * a 4-dimensional simplex is a 5-cell. Specifically, a -simplex is a -dimensional polytope that is the convex hull of its vertices. More formally, suppose the points u_0, \dots, u_k are affinely independent, which means that the vectors u_1 - u_0,\dots, u_k-u_0 are linearly independent. Then, the simplex determined by them is the set of points C = \left\. A regular simplex is a simplex that is also a regular polytope. A regular -simplex may be constructed from a regular -simplex by connecting a new vertex to all original vertices by the common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Range (statistics)
In descriptive statistics, the range of a set of data is size of the narrowest interval which contains all the data. It is calculated as the difference between the largest and smallest values (also known as the sample maximum and minimum). It is expressed in the same units as the data. The range provides an indication of statistical dispersion. Closely related alternative measures are the Interdecile range and the Interquartile range. Range of continuous IID random variables For ''n'' independent and identically distributed continuous random variables ''X''1, ''X''2, ..., ''X''''n'' with the cumulative distribution function G(''x'') and a probability density function g(''x''), let T denote the range of them, that is, T= max(''X''1, ''X''2, ..., ''X''''n'')- min(''X''1, ''X''2, ..., ''X''''n''). Distribution The range, T, has the cumulative distribution function ::F(t)= n \int_^\infty g(x) (x+t)-G(x) \, \textx. Gumbel notes that the "beauty of this formula is com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Pyramid
In mathematics, Pascal's pyramid is a three-dimensional arrangement of the coefficients of the trinomial expansion and the trinomial distribution. Pascal's pyramid is the three-dimensional analog of the two-dimensional Pascal's triangle, which contains the binomial coefficients that appear in the binomial expansion and the binomial distribution. The binomial and trinomial coefficients, expansions, and distributions are subsets of the multinomial constructs with the same names. Structure of the tetrahedron Because the tetrahedron is a three-dimensional object, displaying it on a piece of paper, a computer screen, or other two-dimensional medium is difficult. Assume the tetrahedron is divided into a number of levels, floors, slices, or layers. The top layer (the apex) is labeled "Layer 0". Other layers can be thought of as overhead views of the tetrahedron with the previous layers removed. The first six layers are as follows: The layers of the tetrahedron have been deliberatel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy. The rows of Pascal's triangle are conventionally enumerated starting with row n = 0 at the top (the 0th row). The entries in each row are numbered from the left beginning with k = 0 and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |