function graphing on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, the graph of a function is the set of
In mathematics, the graph of a function is the set of 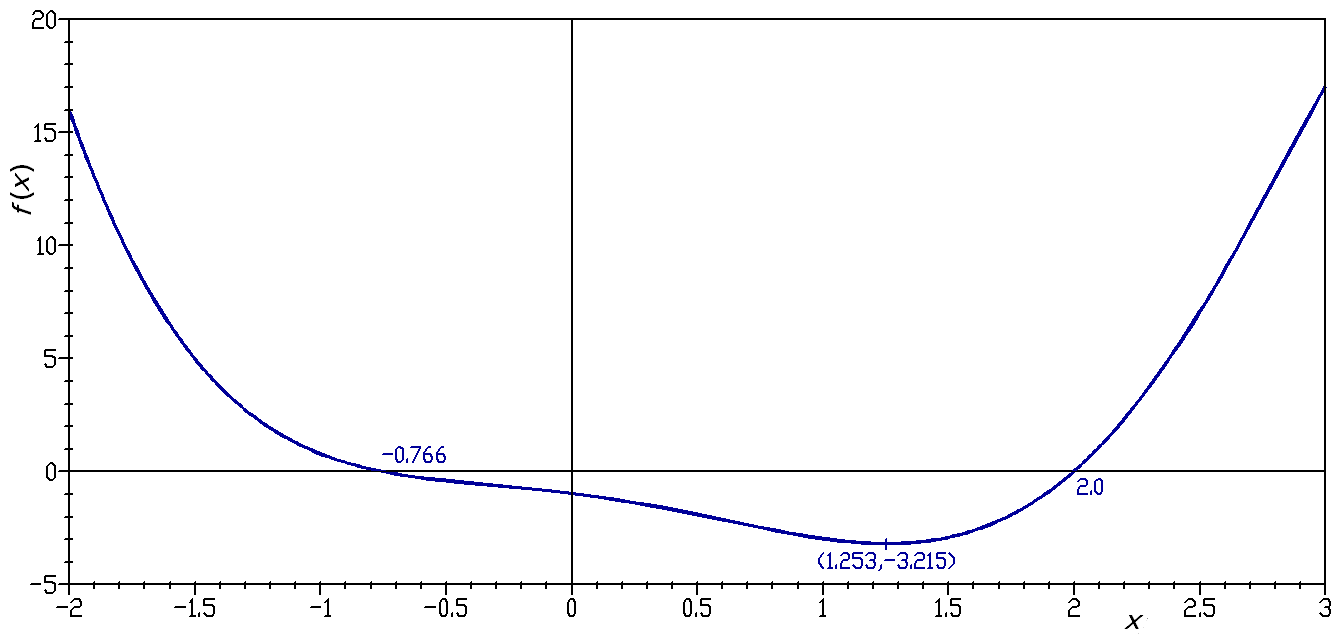
 The graph of the function defined by
is the subset of the set
From the graph, the domain is recovered as the set of first component of each pair in the graph .
Similarly, the range can be recovered as .
The codomain , however, cannot be determined from the graph alone.
The graph of the cubic polynomial on the
The graph of the function defined by
is the subset of the set
From the graph, the domain is recovered as the set of first component of each pair in the graph .
Similarly, the range can be recovered as .
The codomain , however, cannot be determined from the graph alone.
The graph of the cubic polynomial on the
 The graph of the
The graph of the
Function Graph
" From MathWorld—A Wolfram Web Resource. {{Visualization Charts Functions and mappings Numerical function drawing
ordered pair
In mathematics, an ordered pair (''a'', ''b'') is a pair of objects. The order in which the objects appear in the pair is significant: the ordered pair (''a'', ''b'') is different from the ordered pair (''b'', ''a'') unless ''a'' = ''b''. (In co ...
s , where In the common case where and are real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
s, these pairs are Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured i ...
of points in two-dimensional space
In mathematics, a plane is a Euclidean ( flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as ...
and thus form a subset of this plane.
In the case of functions of two variables, that is functions whose domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
** Domain of definition of a partial function
**Natural domain of a partial function
**Domain of holomorphy of a function
*Do ...
consists of pairs the graph usually refers to the set of ordered triples where instead of the pairs as in the definition above. This set is a subset of three-dimensional space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal ...
; for a continuous real-valued function
In mathematics, a real-valued function is a function whose values are real numbers. In other words, it is a function that assigns a real number to each member of its domain.
Real-valued functions of a real variable (commonly called ''real ...
of two real variables, it is a surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is t ...
.
In science
Science is a systematic endeavor that Scientific method, builds and organizes knowledge in the form of Testability, testable explanations and predictions about the universe.
Science may be as old as the human species, and some of the earli ...
, engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, technology
Technology is the application of knowledge to reach practical goals in a specifiable and reproducible way. The word ''technology'' may also mean the product of such an endeavor. The use of technology is widely prevalent in medicine, scie ...
, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see ''Plot (graphics)
A plot is a graphical technique for representing a data set, usually as a graph showing the relationship between two or more variables. The plot can be drawn by hand or by a computer. In the past, sometimes mechanical or electronic plotters were ...
'' for details.
A graph of a function is a special case of a relation.
In the modern foundations of mathematics
Foundations of mathematics is the study of the philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathe ...
, and, typically, in set theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concer ...
, a function is actually equal to its graph. However, it is often useful to see functions as mappings, which consist not only of the relation between input and output, but also which set is the domain, and which set is the codomain
In mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation . The term range is sometimes ambiguously used to refer to either ...
. For example, to say that a function is onto (surjective
In mathematics, a surjective function (also known as surjection, or onto function) is a function that every element can be mapped from element so that . In other words, every element of the function's codomain is the image of one element of ...
) or not the codomain should be taken into account. The graph of a function on its own doesn't determine the codomain. It is common to use both terms ''function'' and ''graph of a function'' since even if considered the same object, they indicate viewing it from a different perspective.
Definition
Given a mapping in other words a function together with its domain and codomain the graph of the mapping is the set which is a subset of . In the abstract definition of a function, is actually equal to One can observe that, if, then the graph is a subset of (strictly speaking it is but one can embed it with the natural isomorphism).Examples
Functions of one variable
 The graph of the function defined by
is the subset of the set
From the graph, the domain is recovered as the set of first component of each pair in the graph .
Similarly, the range can be recovered as .
The codomain , however, cannot be determined from the graph alone.
The graph of the cubic polynomial on the
The graph of the function defined by
is the subset of the set
From the graph, the domain is recovered as the set of first component of each pair in the graph .
Similarly, the range can be recovered as .
The codomain , however, cannot be determined from the graph alone.
The graph of the cubic polynomial on the real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
is
If this set is plotted on a Cartesian plane
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured i ...
, the result is a curve (see figure).
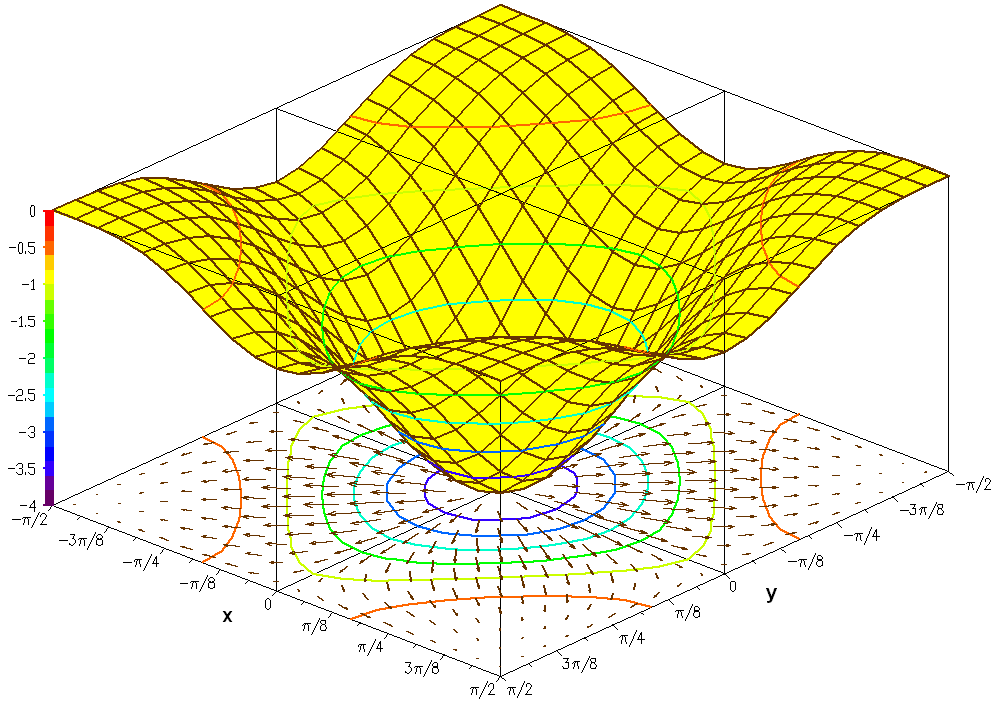
Functions of two variables
trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in ...
is
If this set is plotted on a three dimensional Cartesian coordinate system, the result is a surface (see figure).
Oftentimes it is helpful to show with the graph, the gradient of the function and several level curves. The level curves can be mapped on the function surface or can be projected on the bottom plane. The second figure shows such a drawing of the graph of the function:
See also
*Asymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...
* Chart
* Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.
Definition
A real-valued function f on an ...
* Convex function
In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of the function lies above the graph between the two points. Equivalently, a function is convex if its epigraph (the set of poin ...
* Contour plot
* Critical point
* Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
* Epigraph
* Normal to a graph
* Slope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is used ...
* Stationary point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" i ...
* Tetraview
* Vertical translation
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction. A translation can also be interpreted as the addition of a constant vector to eve ...
* y-intercept
In analytic geometry, using the common convention that the horizontal axis represents a variable ''x'' and the vertical axis represents a variable ''y'', a ''y''-intercept or vertical intercept is a point where the graph of a function or relati ...
References
*External links
* Weisstein, Eric W.Function Graph
" From MathWorld—A Wolfram Web Resource. {{Visualization Charts Functions and mappings Numerical function drawing