Finger Tree on:
[Wikipedia]
[Google]
[Amazon]
In
 Ralf Hinze and Ross Paterson state a finger tree is a functional representation of persistent sequences that can access the ends in amortized constant time. Concatenation and splitting can be done in logarithmic time in the size of the smaller piece. The structure can also be made into a general purpose data structure by defining the split operation in a general form, allowing it to act as a sequence, priority queue, search tree, or priority search queue, among other varieties of abstract data types..
A ''finger'' is a point where one can access ''part'' of a data structure; in imperative languages, this is called a pointer. In a finger tree, the fingers are structures that point to the ends of a sequence, or the leaf nodes. The fingers are added on to the original tree to allow for constant time access to fingers. In the images shown below, the fingers are the lines reaching out of the spine to the nodes.
A finger tree is composed of different ''layers'' which can be identified by the nodes along its ''spine''. The spine of a tree can be thought of as the trunk in the same way trees have leaves and a root. Though finger trees are often shown with the spine and branches coming off the sides, there are actually two nodes on the spine at each level that have been paired to make this central spine. The ''prefix'' is on the left of the spine, while the ''suffix'' is on the right. Each of those nodes has a link to the next level of the spine until they reach the root.
Ralf Hinze and Ross Paterson state a finger tree is a functional representation of persistent sequences that can access the ends in amortized constant time. Concatenation and splitting can be done in logarithmic time in the size of the smaller piece. The structure can also be made into a general purpose data structure by defining the split operation in a general form, allowing it to act as a sequence, priority queue, search tree, or priority search queue, among other varieties of abstract data types..
A ''finger'' is a point where one can access ''part'' of a data structure; in imperative languages, this is called a pointer. In a finger tree, the fingers are structures that point to the ends of a sequence, or the leaf nodes. The fingers are added on to the original tree to allow for constant time access to fingers. In the images shown below, the fingers are the lines reaching out of the spine to the nodes.
A finger tree is composed of different ''layers'' which can be identified by the nodes along its ''spine''. The spine of a tree can be thought of as the trunk in the same way trees have leaves and a root. Though finger trees are often shown with the spine and branches coming off the sides, there are actually two nodes on the spine at each level that have been paired to make this central spine. The ''prefix'' is on the left of the spine, while the ''suffix'' is on the right. Each of those nodes has a link to the next level of the spine until they reach the root.
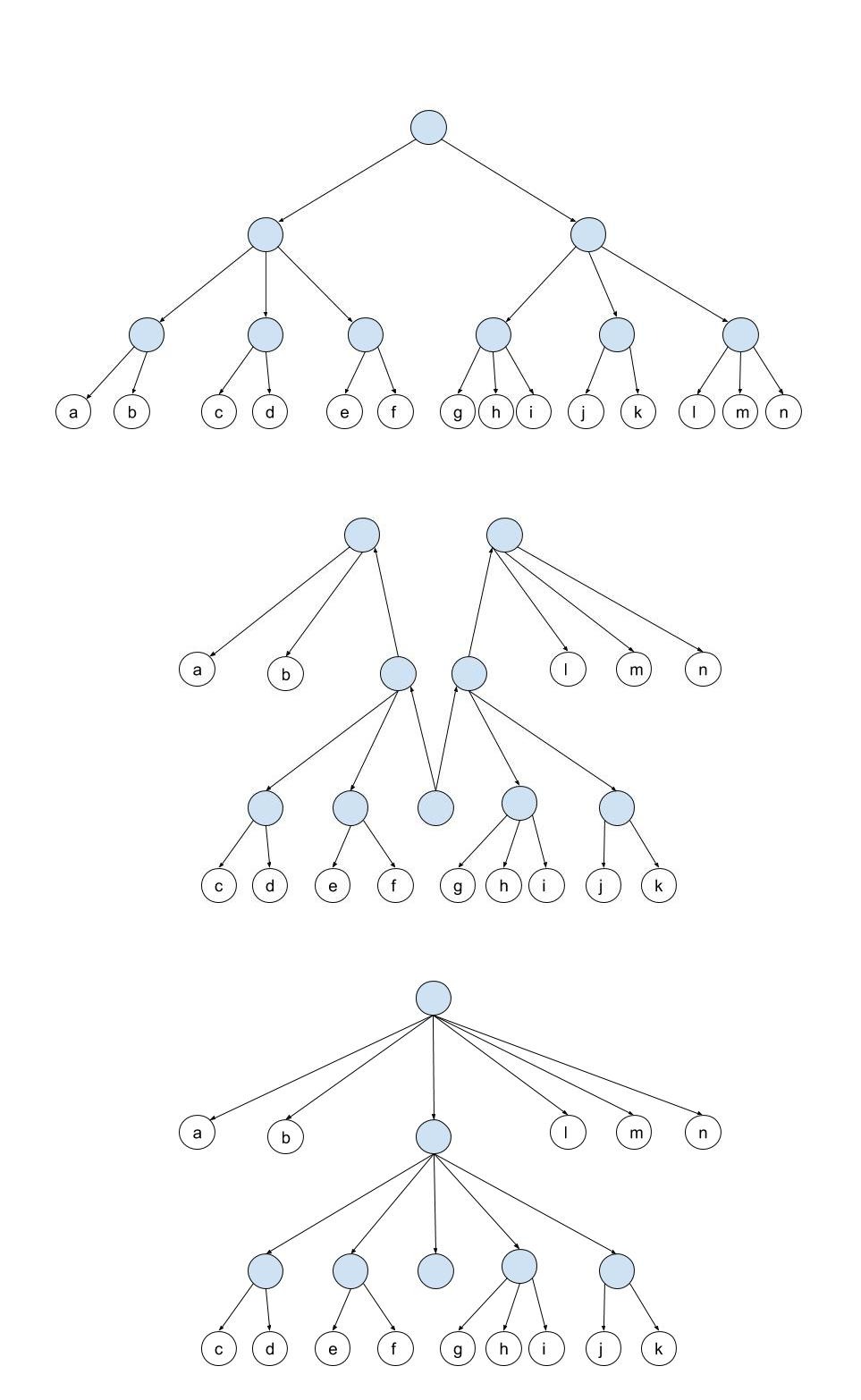 The first level of the tree contains only values, the leaf nodes of the tree, and is of depth 0. The second level is of depth 1. The third is of depth 2 and so on. The closer to the root, the deeper the subtrees of the original tree (the tree before it was a finger tree) the nodes points to. In this way, working down the tree is going from the leaves to the root of the tree, which is the opposite of the typical tree data structure. To get this nice and unusual structure, we have to make sure the original tree has a uniform depth. To ensure that the depth is uniform, when declaring the node object, it must be parameterized by the type of the child. The nodes on the spine of depth 1 and above point to trees, and with this parameterization they can be represented by the nested nodes.
The first level of the tree contains only values, the leaf nodes of the tree, and is of depth 0. The second level is of depth 1. The third is of depth 2 and so on. The closer to the root, the deeper the subtrees of the original tree (the tree before it was a finger tree) the nodes points to. In this way, working down the tree is going from the leaves to the root of the tree, which is the opposite of the typical tree data structure. To get this nice and unusual structure, we have to make sure the original tree has a uniform depth. To ensure that the depth is uniform, when declaring the node object, it must be parameterized by the type of the child. The nodes on the spine of depth 1 and above point to trees, and with this parameterization they can be represented by the nested nodes.
data FingerTree a
= Empty
, Single a
, Deep (Digit a) (FingerTree (Node a)) (Digit a)
data Node a
= Node2 a a
, Node3 a a a
The digits in the examples shown are the nodes with letters. Each list is divided by the prefix or suffix of each node on the spine. In a transformed 2–3 tree it seems that the digit lists at the top level can have a length of two or three with the lower levels only having length of one or two. In order for some application of finger trees to run so efficiently, finger trees allow between one and four subtrees on each level.
The digits of the finger tree can be transformed into a list like so:
type Digit a = One a , Two a a , Three a a a , Four a a a a
And so on the image, the top level has elements of type ''a'', the next has elements of type ''Node a'' because the node in between the spine and leaves, and this would go on meaning in general that the ''n''th level of the tree has elements of type ''a'', or 2–3 trees of depth n. This means a sequence of ''n'' elements is represented by a tree of depth Θ(log ''n''). Even better, an element ''d'' places from the nearest end is stored at a depth of Θ(log d) in the tree.
newtype Size = Size
deriving (Eq, Ord)
instance Monoid Size where
∅ = Size 0
Size m ⊕ Size n = Size (m + n)
The ''N'' is for natural numbers. The new type is needed because the type is the carrier of different monoids. Another new type is still needed for the elements in the sequence, shown below.
newtype Elem a = Elem
newtype Seq a = Seq (FingerTree Size (Elem a))
instance Measured (Elem a) Size where
, , Elem, , = Size 1
These lines of code show that instance works a base case for measuring the sizes and the elements are of size one. The use of newtypes doesn't cause a run-time penalty in Haskell because in a library, the ''Size'' and ''Elem'' types would be hidden from the user with wrapper functions.
With these changes, the length of a sequence can now be computed in constant time.
Example of 2–3 trees in C#
Example of Hinze/Paterson Finger Trees in Java
Example of Hinze/Paterson Finger Trees in C#
Finger tree library for Clojure
Finger tree in Scalaz
{{CS-Trees Trees (data structures) Functional data structures Amortized data structures
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, a finger tree is a purely functional data structure
In computer science, a purely functional data structure is a data structure that can be directly implemented in a purely functional language. The main difference between an arbitrary data structure and a purely functional one is that the latter ...
that can be used to efficiently implement other functional data structures. A finger tree gives amortized constant time access to the "fingers" (leaves) of the tree, which is where data is stored, and concatenation and splitting logarithmic time in the size of the smaller piece. It also stores in each internal node the result of applying some associative operation
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement for express ...
to its descendants. This "summary" data stored in the internal nodes can be used to provide the functionality of data structures other than trees.
Overview
 Ralf Hinze and Ross Paterson state a finger tree is a functional representation of persistent sequences that can access the ends in amortized constant time. Concatenation and splitting can be done in logarithmic time in the size of the smaller piece. The structure can also be made into a general purpose data structure by defining the split operation in a general form, allowing it to act as a sequence, priority queue, search tree, or priority search queue, among other varieties of abstract data types..
A ''finger'' is a point where one can access ''part'' of a data structure; in imperative languages, this is called a pointer. In a finger tree, the fingers are structures that point to the ends of a sequence, or the leaf nodes. The fingers are added on to the original tree to allow for constant time access to fingers. In the images shown below, the fingers are the lines reaching out of the spine to the nodes.
A finger tree is composed of different ''layers'' which can be identified by the nodes along its ''spine''. The spine of a tree can be thought of as the trunk in the same way trees have leaves and a root. Though finger trees are often shown with the spine and branches coming off the sides, there are actually two nodes on the spine at each level that have been paired to make this central spine. The ''prefix'' is on the left of the spine, while the ''suffix'' is on the right. Each of those nodes has a link to the next level of the spine until they reach the root.
Ralf Hinze and Ross Paterson state a finger tree is a functional representation of persistent sequences that can access the ends in amortized constant time. Concatenation and splitting can be done in logarithmic time in the size of the smaller piece. The structure can also be made into a general purpose data structure by defining the split operation in a general form, allowing it to act as a sequence, priority queue, search tree, or priority search queue, among other varieties of abstract data types..
A ''finger'' is a point where one can access ''part'' of a data structure; in imperative languages, this is called a pointer. In a finger tree, the fingers are structures that point to the ends of a sequence, or the leaf nodes. The fingers are added on to the original tree to allow for constant time access to fingers. In the images shown below, the fingers are the lines reaching out of the spine to the nodes.
A finger tree is composed of different ''layers'' which can be identified by the nodes along its ''spine''. The spine of a tree can be thought of as the trunk in the same way trees have leaves and a root. Though finger trees are often shown with the spine and branches coming off the sides, there are actually two nodes on the spine at each level that have been paired to make this central spine. The ''prefix'' is on the left of the spine, while the ''suffix'' is on the right. Each of those nodes has a link to the next level of the spine until they reach the root.
 The first level of the tree contains only values, the leaf nodes of the tree, and is of depth 0. The second level is of depth 1. The third is of depth 2 and so on. The closer to the root, the deeper the subtrees of the original tree (the tree before it was a finger tree) the nodes points to. In this way, working down the tree is going from the leaves to the root of the tree, which is the opposite of the typical tree data structure. To get this nice and unusual structure, we have to make sure the original tree has a uniform depth. To ensure that the depth is uniform, when declaring the node object, it must be parameterized by the type of the child. The nodes on the spine of depth 1 and above point to trees, and with this parameterization they can be represented by the nested nodes.
The first level of the tree contains only values, the leaf nodes of the tree, and is of depth 0. The second level is of depth 1. The third is of depth 2 and so on. The closer to the root, the deeper the subtrees of the original tree (the tree before it was a finger tree) the nodes points to. In this way, working down the tree is going from the leaves to the root of the tree, which is the opposite of the typical tree data structure. To get this nice and unusual structure, we have to make sure the original tree has a uniform depth. To ensure that the depth is uniform, when declaring the node object, it must be parameterized by the type of the child. The nodes on the spine of depth 1 and above point to trees, and with this parameterization they can be represented by the nested nodes.
Transforming a tree into a finger tree
We will start this process with a balanced 2–3 tree. For the finger tree to work, all the leaf nodes need to also be level. A finger is "a structure providing efficient access to nodes of a tree near a distinguished location." To make a finger tree we need to put fingers to the right and left ends of the tree and transform it like azipper
A zipper (N. America), zip, zip fastener (UK), formerly known as a clasp locker, is a commonly used device for binding together two edges of textile, fabric or other flexible material. Used in clothing (e.g. jackets and jeans), luggage and oth ...
. This gives us that constant amortized time access to the ends of a sequence.
To transform, start with the balanced 2–3 tree.
Take the leftmost and rightmost internal nodes of the tree and pull them up so the rest of the tree dangles between them as shown in the image to the right.
Combines the spines to make a standard 2–3 finger tree.
This can be described as:
Reductions
Deque operations
Finger trees also make efficient deques. Whether the structure is persistent or not, all operations take Θ(1) amortized time. The analysis can be compared to Okasaki's implicit deques, the only difference being that the FingerTree type stores Nodes instead of pairs.Application
Finger trees can be used to build other trees. For example, apriority queue
In computer science, a priority queue is an abstract data type similar to a regular queue (abstract data type), queue or stack (abstract data type), stack abstract data type.
In a priority queue, each element has an associated ''priority'', which ...
can be implemented by labeling the internal nodes by the minimum priority of its children in the tree, or an indexed list/array can be implemented with a labeling of nodes by the count of the leaves in their children. Other applications are random-access sequences, described below, ordered sequences, and interval trees.
Finger trees can provide amortized O(1) pushing, reversing, popping, O(log n) append and split; and can be adapted to be indexed or ordered sequences. And like all functional data structures, it is inherently persistent; that is, older versions of the tree are always preserved.
Random-access sequences
Finger trees can efficiently implement random-access sequences. This should support fast positional operations including accessing the ''n''th element and splitting a sequence at a certain position. To do this, we annotate the finger tree with sizes.First publication
Finger trees were first published in 1977 by Leonidas J. Guibas, and periodically refined since (e.g. a version using AVL trees, non-lazy finger trees, simpler 2–3 finger trees shown here, B-Trees and so on)Implementations
Finger trees have since been used in theHaskell
Haskell () is a general-purpose, statically typed, purely functional programming language with type inference and lazy evaluation. Designed for teaching, research, and industrial applications, Haskell pioneered several programming language ...
core libraries (in the implementation of ''Data.Sequence''), and an implementation in OCaml
OCaml ( , formerly Objective Caml) is a General-purpose programming language, general-purpose, High-level programming language, high-level, Comparison of multi-paradigm programming languages, multi-paradigm programming language which extends the ...
exists which was derived from a proven-correct Coq implementation. There is also a verified implementation in Isabelle (proof assistant)
The Isabelle automated theorem prover is a higher-order logic (HOL) theorem prover, written in Standard ML and Scala. As a Logic for Computable Functions (LCF) style theorem prover, it is based on a small logical core (kernel) to increase the ...
from which programs in Haskell and other (functional) languages can be generated. Finger trees can be implemented with or without lazy evaluation
In programming language theory, lazy evaluation, or call-by-need, is an evaluation strategy which delays the evaluation of an Expression (computer science), expression until its value is needed (non-strict evaluation) and which avoids repeated eva ...
,. but laziness allows for simpler implementations.
See also
*Monoid
In abstract algebra, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being .
Monoids are semigroups with identity ...
* Finger search tree
In computer science, finger search trees are a type of binary search tree that keeps pointers to interior nodes, called ''fingers''. The fingers speed up searches, insertions, and deletions for elements close to the fingers, giving amortized O ...
* Zippers
References
External links
* http://www.soi.city.ac.uk/~ross/papers/FingerTree.html * http://hackage.haskell.org/packages/archive/EdisonCore/1.2.1.1/doc/html/Data-Edison-Concrete-FingerTree.htmlExample of 2–3 trees in C#
Example of Hinze/Paterson Finger Trees in Java
Example of Hinze/Paterson Finger Trees in C#
Finger tree library for Clojure
Finger tree in Scalaz
{{CS-Trees Trees (data structures) Functional data structures Amortized data structures