Euclidean minimum spanning tree

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

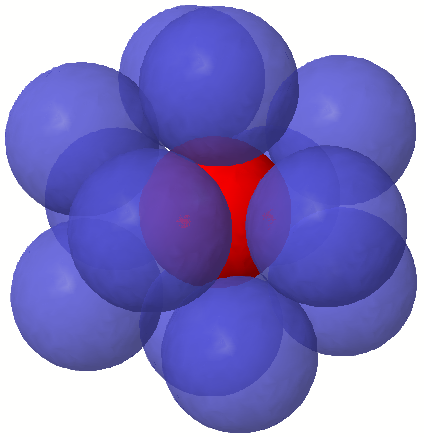
The edges of the minimum spanning tree meet at angles of at least 60°, at most six to a vertex. In higher dimensions, the number of edges per vertex is bounded by the kissing number of tangent unit spheres. The total length of the edges, for points in a unit square, is at most proportional to the square root of the number of points. Each edge lies in an empty region of the plane, and these regions can be used to prove that the Euclidean minimum spanning tree is a subgraph of other geometric graphs including the relative neighborhood graph and Delaunay triangulation. By constructing the Delaunay triangulation and then applying a graph minimum spanning tree algorithm, the minimum spanning tree of $n$ given planar points may be found in time $O(n\log n)$, as expressed in big O notation. This is optimal in some models of computation, although faster randomized algorithms exist for points with integer coordinates. For points in higher dimensions, finding an optimal algorithm remains an open problem.

Definition and related problems

A Euclidean minimum spanning tree, for a set of $n$ points in the Euclidean plane or Euclidean space, is a system of line segments, having only the given points as their endpoints, whose union includes all of the points in a connected set, and which has the minimum possible total length of any such system. Such a network cannot contain a polygonal ring of segments; if one existed, the network could be shortened by removing an edge of the polygon. Therefore, the minimum-length network forms a tree. This observation leads to the equivalent definition that a Euclidean minimum spanning tree is a tree of line segments between pairs of the given points, of minimum total length. The same tree may also be described as a minimum spanning tree of a weighted complete graph, having the given points as its vertices and the distances between points as edge weights. The same points may have more than one minimum spanning tree. For instance, for the vertices of a regular polygon, removing any edge of the polygon produces a minimum spanning tree.

Publications on the Euclidean minimum spanning tree commonly abbreviate it as "EMST". They may also be called "geometric minimum spanning trees", but that term may be used more generally for geometric spaces with non-Euclidean distances, such as spaces. When the context of Euclidean point sets is clear, they may be called simply "minimum spanning trees".

Several other standard geometric networks are closely related to the Euclidean minimum spanning tree:
*The Steiner tree problem again seeks a system of line segments connecting all given points, but without requiring the segments to start and end only at given points. In this problem, additional points may be added as segment endpoints, allowing the Steiner tree to be shorter than the minimum spanning tree.
*In the Euclidean traveling salesperson path problem, the connecting line segments must start and end at the given points, like the spanning tree and unlike the Steiner tree; additionally, each point can touch at most two line segments, so the result forms a polygonal chain. Because of this restriction, the optimal path may be longer than the Euclidean minimum spanning tree, but is at most twice as long.
*Geometric spanners are low-weight networks that, like the minimum spanning tree, connect all of the points. Unlike the minimum spanning tree, all of these connecting paths are required to be short, having length proportional to the distance between the points they connect. To achieve this property, these networks generally have cycles and so are not trees.

Properties

Angles and vertex degrees

Whenever two edges of a Euclidean minimum spanning tree meet at a vertex, they must form an angle of 60° or more, with equality only when they form two sides of an equilateral triangle. This is because, for two edges forming any sharper angle, one of the two edges could be replaced by the third, shorter edge of the triangle they form, forming a tree with smaller total length. In comparison, the Steiner tree problem has a stronger angle bound: an optimal Steiner tree has all angles at least 120°.

The same 60° angle bound also occurs in the kissing number problem, of finding the maximum number of unit spheres in Euclidean space that can be tangent to a central unit sphere without any two spheres intersecting (beyond a point of tangency). The center points of these spheres have a minimum spanning tree in the form of a star, with the central point adjacent to all other points. Conversely, for any vertex $v$ of any minimum spanning tree, one can construct non-overlapping unit spheres centered at $v$ and at points two units along each of its edges, with a tangency for each neighbor of $v$. Therefore, in $n$-dimensional space the maximum possible degree of a vertex (the number of spanning tree edges connected to it) equals the kissing number of spheres in $n$ dimensions. Planar minimum spanning trees have degree at most six, and when a tree has degree six there is always another minimum spanning tree with maximum degree five. Three-dimensional minimum spanning trees have degree at most twelve. The only higher dimensions in which the exact value of the kissing number is known are four, eight, and 24 dimensions.

For points generated at random from a given continuous distribution, the minimum spanning tree is almost surely unique. The numbers of vertices of any given degree converge, for large number of vertices, to a constant times that number of vertices. The values of these constants depend on the degree and the distribution. However, even for simple cases—such as the number of leaves for points uniformly distributed in a unit square—their precise values are not known.

Empty regions

For any edge $uv$ of any Euclidean minimum spanning tree, the lens (or vesica piscis) formed by intersecting the two circles with $uv$ as their radii cannot have any other given vertex $w$ in its interior. Put another way, if any tree has an edge $uv$ whose lens contains a third point $w$, then it is not of minimum length. For, by the geometry of the two circles, $w$ would be closer to both $u$ and $v$ than they are to each other. If edge $uv$ were removed from the tree, $w$ would remain connected to one of $u$ and $v$, but not the other. Replacing the removed edge $uv$ by $uw$ or $vw$ (whichever of these two edges reconnects $w$ to the vertex from which it was disconnected) would produce a shorter tree.

For any edge $uv$ of any Euclidean minimum spanning tree, the rhombus with angles of 60° and 120°, having $uv$ as its long diagonal, is disjoint from the rhombi formed analogously by all other edges. Two edges sharing an endpoint cannot have overlapping rhombi, because that would imply a edge angle sharper than 60°, and two disjoint edges cannot have overlapping rhombi; if they did, the longer of the two edges could be replaced by a shorter edge among the same four vertices.

Supergraphs

Certain geometric graphs have definitions involving empty regions in point sets, from which it follows that they contain every edge that can be part of a Euclidean minimum spanning tree. These include:
*The relative neighborhood graph, which has an edge between any pair of points whenever the lens they define is empty.
*The Gabriel graph, which has an edge between any pair of points whenever the circle having the pair as a diameter is empty.
*The Delaunay triangulation, which has an edge between any pair of points whenever there exists an empty circle having the pair as a chord.
*The Urquhart graph, formed from the Delaunay triangulation by removing the longest edge of each triangle. For each remaining edge, the vertices of the Delaunay triangles that use that edge cannot lie within the empty lune of the relative neighborhood graph.
Because the empty-region criteria for these graphs are progressively weaker, these graphs form an ordered sequence of subgraphs. That is, using "⊆" to denote the subset relationship among their edges, these graphs have the relations:

Another graph guaranteed to contain the minimum spanning tree is the Yao graph, determined for points in the plane by dividing the plane around each point into six 60° wedges and connecting each point to the nearest neighbor in each wedge. The resulting graph contains the relative neighborhood graph, because two vertices with an empty lens must be the nearest neighbors to each other in their wedges. As with many of the other geometric graphs above, this definition can be generalized to higher dimensions, and (unlike the Delaunay triangulation) its generalizations always include a linear number of edges.

Total length

For $n$ points in the unit square (or any other fixed shape), the total length of the minimum spanning tree edges is $O(\sqrt n)$. Some sets of points, such as points evenly spaced in a $\sqrt n \times \sqrt n$ grid, attain this bound. For points in a unit hypercube in $d$-dimensional space, the corresponding bound is $O(n^)$. The same bound applies to the expected total length of the minimum spanning tree for $n$ points chosen uniformly and independently from a unit square or unit hypercube. Returning to the unit square, the sum of squared edge lengths of the minimum spanning tree is $O(1)$. This bound follows from the observation that the edges have disjoint rhombi, with area proportional to the edge lengths squared. The $O(\sqrt n)$ bound on total length follows by application of the Cauchy–Schwarz inequality.

Another interpretation of these results is that the average edge length for any set of points in a unit square is $O(1/\sqrt n)$, at most proportional to the spacing of points in a regular grid; and that for ''random'' points in a unit square the average length is proportional to $1/\sqrt n$. However, in the random case, with high probability the longest edge has length approximately $\sqrt,$ longer than the average by a non-constant factor. With high probability, the longest edge forms a leaf of the spanning tree, and connects a point far from all the other points to its nearest neighbor. For large numbers of points, the distribution of the longest edge length around its expected value converges to a Laplace distribution.

Any geometric spanner, a subgraph of a complete geometric graph whose shortest paths approximate the Euclidean distance, must have total edge length at least as large as the minimum spanning tree, and one of the standard quality measures for a geometric spanner is the ratio between its total length and of the minimum spanning tree for the same points. Several methods for constructing spanners, such as the greedy geometric spanner, achieve a constant bound for this ratio. It has been conjectured that the Steiner ratio, the largest possible ratio between the total length of a minimum spanning tree and Steiner tree for the same set of points in the plane, is $2/\sqrt\approx 1.1547$, the ratio for three points in an equilateral triangle.

Subdivision

If every edge of a Euclidean minimum spanning tree is subdivided, by adding a new point at its midpoint, then the resulting tree is still a minimum spanning tree of the augmented point set. Repeating this subdivision process allows a Euclidean minimum spanning tree to be subdivided arbitrarily finely. However, subdividing only some of the edges, or subdividing the edges at points other than the midpoint, may produce a point set for which the subdivided tree is not the minimum spanning tree.

Computational complexity

For points in any dimension, the minimum spanning tree can be constructed in time $O(n^2)$ by constructing a complete graph with an edge between every pair of points, weighted by Euclidean distance, and then applying a graph minimum spanning tree algorithm such as the Prim–Dijkstra–Jarník algorithm or Borůvka's algorithm on it. These algorithms can be made to take time $O(n^2)$ on complete graphs, unlike another common choice, Kruskal's algorithm, which is slower because it involves sorting all distances. For points in low-dimensional spaces, the problem may be solved more quickly, as detailed below.

Computing Euclidean distances involves a square root calculation. In any comparison of edge weights, comparing the squares of the Euclidean distances, instead of the distances themselves, yields the same ordering, and so does not change the rest of the tree's computation. This shortcut speeds up calculation and allows a minimum spanning tree for points with integer coordinates to be constructed using only integer arithmetic.

Two dimensions

A faster approach to finding the minimum spanning tree of planar points uses the property that it is a subgraph of the Delaunay triangulation:
# Compute the Delaunay triangulation, which can be done in $O(n\log n)$ time. Because the Delaunay triangulation is a planar graph, it has at most $3n-6$ edges.
# Label each edge with its (squared) length.
# Run a graph minimum spanning tree algorithm. Since there are $O(n)$ edges, this requires $O(n\log n)$ time using any of the standard minimum spanning tree algorithms.
The result is an algorithm taking $O(n\log n)$ time, optimal in certain models of computation (see below).

If the input coordinates are integers and can be used as array indices, faster algorithms are possible: the Delaunay triangulation can be constructed by a randomized algorithm in $O(n\log\log n)$ expected time. Additionally, since the Delaunay triangulation is a planar graph, its minimum spanning tree can be found in linear time by a variant of Borůvka's algorithm that removes all but the cheapest edge between each pair of components after each stage of the algorithm. Therefore, the total expected time for this algorithm is $O(n\log\log n)$. In the other direction, the Delaunay triangulation can be constructed from the minimum spanning tree in the near-linear time bound $O(n\log^* n)$, where $\log^*$ denotes the iterated logarithm.

Higher dimensions

The problem can also be generalized to $n$ points in the $d$-dimensional space $\R^d$. In higher dimensions, the connectivity determined by the Delaunay triangulation (which, likewise, partitions the convex hull into $d$-dimensional simplices) contains the minimum spanning tree; however, the triangulation might contain the complete graph. Therefore, finding the Euclidean minimum spanning tree as a spanning tree of the complete graph or as a spanning tree of the Delaunay triangulation both take $O(dn^2)$ time. For three dimensions the minimum spanning tree can be found in time $O\bigl((n\log n)^\bigr)$, and in any greater dimension, in time
$O\left(n^\right)$
for any $\varepsilon>0$—faster than the quadratic time bound for the complete graph and Delaunay triangulation algorithms.

The optimal time complexity for higher-dimensional minimum spanning trees remains unknown, but is closely related to the complexity of computing ''bichromatic closest pairs''. In the bichromatic closest pair problem, the input is a set of points, given two different colors (say, red and blue). The output is a pair of a red point and a blue point with the minimum possible distance. This pair always forms one of the edges in the minimum spanning tree. Therefore, the bichromatic closest pair problem can be solved in the amount of time that it takes to construct a minimum spanning tree and scan its edges for the shortest red–blue edge. Conversely, for any red–blue coloring of any subset of a given set of points, the bichromatic closest pair produces one edge of the minimum spanning tree of the subset. By carefully choosing a sequence of colorings of subsets, and finding the bichromatic closest pair of each subproblem, the minimum spanning tree may be found in time proportional to the optimal time for finding bichromatic closest pairs for the same number of points, whatever that optimal time turns out to be.

For uniformly random point sets in any bounded dimension, the Yao graph or Delaunay triangulation have linear expected numbers of edges, are guaranteed to contain the minimum spanning tree, and can be constructed in linear expected time. From these graphs, the minimum spanning tree itself may be constructed in linear time, by using a randomized linear time algorithm for graph minimum spanning trees. However, the poor performance of these methods on inputs coming from clustered data has led algorithm engineering researchers to develop methods with a somewhat slower $O(n\log n)$ time bound, for random inputs or inputs whose distances and clustering resemble those of random data, while exhibiting better performance on real-world data.

A well-separated pair decomposition is a family of pairs of subsets of the given points, so that every pair of points belong to one of these pairs of subsets, and so that all pairs of points coming from the same pair of subsets have approximately the same length. It is possible to find a well-separated pair decomposition with a linear number of subsets, and a representative pair of points for each subset, in time $O(n\log n)$. The minimum spanning tree of the graph formed by these representative pairs is then an approximation to the minimum spanning tree. Using these ideas, a $(1+\varepsilon)$-approximation to the minimum spanning tree may be found in $O(n\log n)$ time, for constant $\varepsilon$. More precisely, by choosing each representative pair to approximate the closest pair in its equivalence class, and carefully varying the quality of this approximation for different pairs, the dependence on $\varepsilon$ in the time bound can be given as $O(n \log n + (\varepsilon^ \log ^2 \tfrac)n),$ for any fixed dimension.

Dynamic and kinetic

The Euclidean minimum spanning tree has been generalized in many different ways to systems of moving or changing points:
*If a set of points undergoes a sequence of dynamic insertions or deletions of points, each of these updates induces a bounded amount of change to the minimum spanning tree of the points. When the update sequence is known in advance, for points in the plane, the change after each insertion or deletion can be found in time $O(\log^2 n)$ per insertion or deletion. When the updates must be handled in an online manner, a slower (but still poly-logarithmic) $O(\log^ n)$ time bound is known. For higher-dimensional versions of the problem the time per update is slower, but still sublinear.
*For $n$ points moving linearly with constant speed, or with more general algebraic motions, the minimum spanning tree will change by a sequence of swaps, in which one edge is removed and another replaces it at a point in time where both have equal length. For linear motions, the number of changes is at most slightly larger than $n^$. For more general algebraic motions, there is a near-cubic upper bound on the number of swaps, based on the theory of Davenport–Schinzel sequences.
*The ''minimum moving spanning tree problem'' again concerns points moving linearly with constant speed, over an interval of time, and seeks a single tree that minimizes the maximum sum of weights occurring at any instant during this interval. It is NP-hard to compute exactly, but can be approximated to within a factor of two in polynomial time.
*The kinetic Euclidean minimum spanning tree problem asks for a kinetic data structure that can maintain the minimum spanning tree as its points undergo both continuous motions and insertions and deletions. Several papers have studied such structures, and a kinetic structure for algebraically moving points with near-cubic total time, nearly matching the bound on the number of swaps, is known.

Lower bound

An asymptotic lower bound of $\Omega(n\log n)$ of the Euclidean minimum spanning tree problem can be established in restricted models of computation. These include the algebraic decision tree and algebraic computation tree models, in which the algorithm has access to the input points only through certain restricted primitives that perform simple algebraic computations on their coordinates. In these models, the closest pair of points problem requires $\Omega(n\log n)$ time, but the closest pair is necessarily an edge of the minimum spanning tree, so the minimum spanning tree also requires this much time. Therefore, algorithms for constructing the planar minimum spanning tree in time $O(n\log n)$ within this model, for instance by using the Delaunay triangulation, are optimal. However, these lower bounds do not apply to models of computation with integer point coordinates, in which bitwise operations and table indexing operations on those coordinates are permitted. In these models, faster algorithms are possible, as described above.

Applications

An obvious application of Euclidean minimum spanning trees is to find the cheapest network of wires or pipes to connect a set of places, assuming the links cost a fixed amount per unit length. The first publications on minimum spanning trees more generally concerned a geographic version of the problem, involving the design of an electrical grid for southern Moravia, and an application to minimizing wire lengths in circuits was described in 1957 by Loberman and Weinberger.

Minimum spanning trees are closely related to single-linkage clustering, one of several methods for hierarchical clustering. The edges of a minimum spanning tree, sorted by their length, give the order in which to merge clusters into larger clusters in this clustering method. Once these edges have been found, by any algorithm, they may be used to construct the single-linkage clustering in time $O(n\log n)$. Although the long thin cluster shapes produced by single-linkage clustering can be a bad fit for certain types of data, such as mixtures of Gaussian distributions, it can be a good choice in applications where the clusters themselves are expected to have long thin shapes, such as in modeling the dark matter halos of galaxies. In geographic information science, several researcher groups have used minimum spanning trees of the centroids of buildings to identify meaningful clusters of buildings, for instance by removing edges identified in some other way as inconsistent.

Minimum spanning trees have also been used to infer the shape of curves in the plane, given points sampled along the curve. For a smooth curve, sampled more finely than its local feature size, the minimum spanning tree will form a path connecting consecutive points along the curve. More generally, similar methods can recognize curves drawn in a dotted or dashed style rather than as a single connected set. Applications of this curve-finding technique include particle physics, in automatically identifying the tracks left by particles in a bubble chamber. More sophisticated versions of this idea can find curves from a cloud of noisy sample points that roughly follows the curve outline, by using the topology of the spanning tree to guide a moving least squares method.

Another application of minimum spanning trees is a constant-factor approximation algorithm for the Euclidean traveling salesman problem, the problem of finding the shortest polygonalization of a point set. Walking around the boundary of the minimum spanning tree can approximate the optimal traveling salesman tour within a factor of two of the optimal length. However, more accurate polynomial-time approximation schemes are known for this problem. In wireless ad hoc networks, broadcasting messages along paths in a minimum spanning tree can be an accurate approximation to the minimum-energy broadcast routing, which is, again, hard to compute exactly.

Realization

The ''realization problem'' for Euclidean minimum spanning trees takes an abstract tree as input and seeks a geometric location for each vertex of the tree (in a space of some fixed dimension), such that the given tree equals the minimum spanning tree of those points. Not every abstract tree has such a realization; for instance, the tree must obey the kissing number bound on the degree of each vertex. Additional restrictions exist; for instance, it is not possible for a planar minimum spanning tree to have a degree-six vertex adjacent to a vertex of degree five or six. Determining whether a two-dimensional realization exists is NP-hard. However, the proof of hardness depends on the fact that degree-six vertices in a tree have a very restricted set of realizations: the neighbors of such a vertex must be placed on the vertices of a regular hexagon centered at that vertex. Indeed, for trees of maximum degree five, a planar realization always exists. Similarly, for trees of maximum degree ten, a three-dimensional realization always exists. For these realizations, some trees may require edges of exponential length and bounding boxes of exponential area relative to the length of their shortest edge. Trees of maximum degree four have smaller planar realizations, with polynomially bounded edge lengths and bounding boxes.

See also

*Rectilinear minimum spanning tree, a minimum spanning tree with distances measured using taxicab geometry

References

External links

EMST tutorial
mlpack documentation

{{DEFAULTSORT:Euclidean Minimum Spanning Tree
Spanning tree
Geometric graphs