Elastic Map on:
[Wikipedia]
[Google]
[Amazon]
 Elastic maps provide a tool for
Elastic maps provide a tool for
A.Y. Zinovyev
and A.A. Pitenko in 1996–1998.
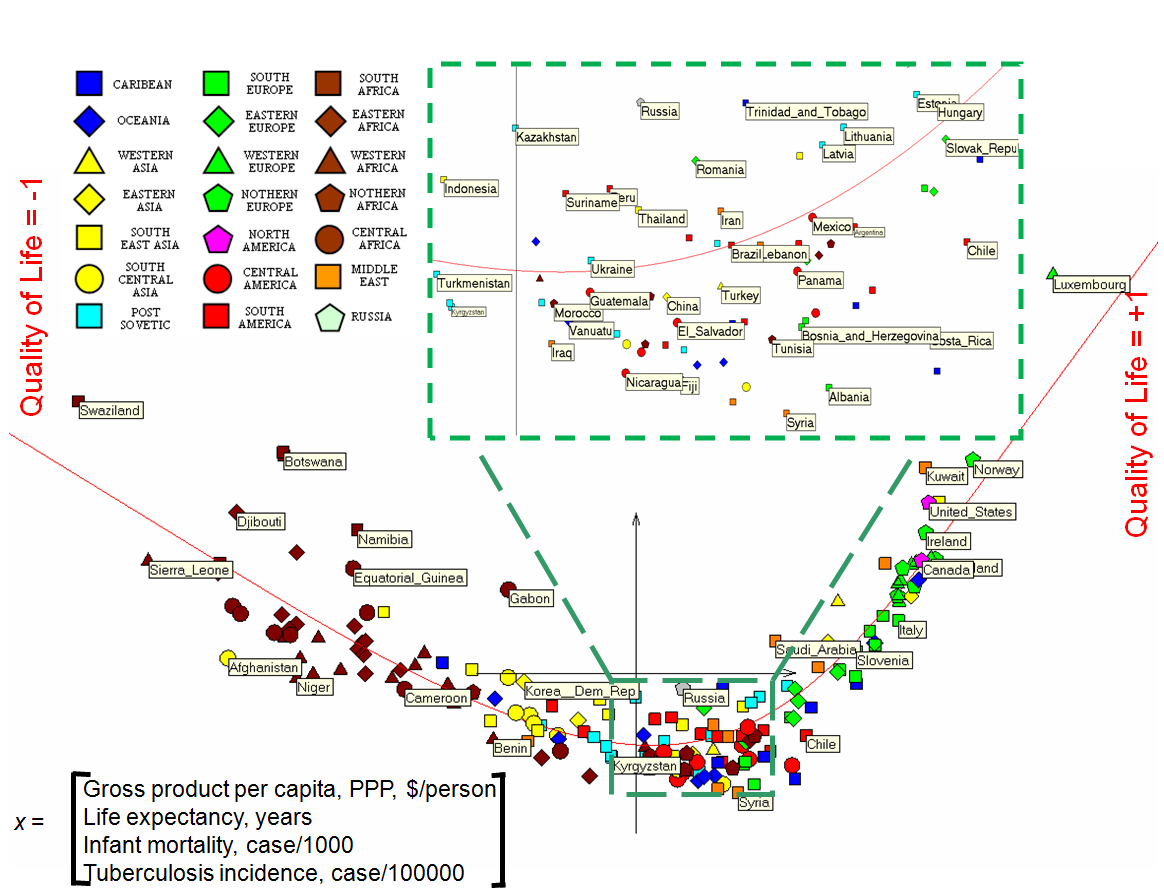 Most important applications of the method and free software are in bioinformatics for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
The method is applied in quantitative biology for reconstructing the curved surface of a tree leaf from a stack of light microscopy images. This reconstruction is used for quantifying the
Most important applications of the method and free software are in bioinformatics for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
The method is applied in quantitative biology for reconstructing the curved surface of a tree leaf from a stack of light microscopy images. This reconstruction is used for quantifying the
Computational Intelligence Paradigms in Economic and Financial Decision Making
Series Intelligent Systems Reference Library, Volume 99, Springer International Publishing, Switzerland 2016. provides a systematic comparison of elastic maps and
 Elastic maps provide a tool for
Elastic maps provide a tool for nonlinear dimensionality reduction
Nonlinear dimensionality reduction, also known as manifold learning, refers to various related techniques that aim to project high-dimensional data onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low- ...
. By their construction, they are a system of elastic springs
Spring(s) may refer to:
Common uses
* Spring (season), a season of the year
* Spring (device), a mechanical device that stores energy
* Spring (hydrology), a natural source of water
* Spring (mathematics), a geometric surface in the shape of a he ...
embedded in the data
space. This system approximates a low-dimensional manifold. The elastic coefficients of this system allow the switch from completely unstructured k-means clustering
''k''-means clustering is a method of vector quantization, originally from signal processing, that aims to partition ''n'' observations into ''k'' clusters in which each observation belongs to the cluster with the nearest mean (cluster centers o ...
(zero elasticity) to the estimators located closely to linear PCA manifolds (for high bending and low stretching modules). With some intermediate values of the elasticity coefficient
The rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, and product concentrations and other effectors. The degree to which these factors change the reaction rate is described by the elasticity ...
s, this system effectively approximates non-linear principal manifolds. This approach is based on a mechanical
Mechanical may refer to:
Machine
* Machine (mechanical), a system of mechanisms that shape the actuator input to achieve a specific application of output forces and movement
* Mechanical calculator, a device used to perform the basic operations of ...
analogy between principal manifolds, that are passing through "the middle" of the data distribution, and elastic membranes and plates. The method was developed by A.N. GorbanA.Y. Zinovyev
and A.A. Pitenko in 1996–1998.
Energy of elastic map
Let be a data set in a finite-dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean sp ...
. Elastic map is represented by a set of nodes in the same space. Each datapoint has a ''host node'', namely the closest node (if there are several closest nodes then one takes the node with the smallest number). The data set is divided into classes .
The ''approximation energy'' D is the distortion
: ,
which is the energy of the springs with unit elasticity which connect each data point with its host node. It is possible to apply weighting factors to the terms of this sum, for example to reflect the standard deviation of the probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) c ...
of any subset of data points .
On the set of nodes an additional structure is defined. Some pairs of nodes, , are connected by ''elastic edges''. Call this set of pairs . Some triplets of nodes, , form ''bending ribs''. Call this set of triplets .
: The stretching energy is ,
: The bending energy is ,
where and are the stretching and bending moduli respectively. The stretching energy is sometimes referred to as the ''membrane'', while the bending energy is referred to as the ''thin plate'' term.
For example, on the 2D rectangular grid the elastic edges are just vertical and horizontal edges (pairs of closest vertices) and the bending ribs are the vertical or horizontal triplets of consecutive (closest) vertices.
: The total energy of the elastic map is thus
The position of the nodes is determined by the mechanical equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is ze ...
of the elastic map, i.e. its location is such that it minimizes the total energy .
Expectation-maximization algorithm
For a given splitting of dataset in classes , minimization of the quadratic functional is a linear problem with the sparse matrix of coefficients. Therefore, similar toprincipal component analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and ...
or k-means
''k''-means clustering is a method of vector quantization, originally from signal processing, that aims to Partition of a set, partition ''n'' observations into ''k'' clusters in which each observation belongs to the Cluster (statistics), cluster ...
, a splitting method is used:
* For given find ;
* For given minimize and find ;
* If no change, terminate.
This expectation-maximization algorithm guarantees a local minimum of . For improving the approximation various additional methods are proposed. For example, the ''softening'' strategy is used. This strategy
starts with a rigid grids (small length, small bending and large elasticity modules
and coefficients) and finishes with soft grids (small and ). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is ''growing net'': one starts from a small number of nodes and gradually adds new nodes. Each epoch goes with its own number of nodes.
Applications
 Most important applications of the method and free software are in bioinformatics for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
The method is applied in quantitative biology for reconstructing the curved surface of a tree leaf from a stack of light microscopy images. This reconstruction is used for quantifying the
Most important applications of the method and free software are in bioinformatics for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.
The method is applied in quantitative biology for reconstructing the curved surface of a tree leaf from a stack of light microscopy images. This reconstruction is used for quantifying the geodesic
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
distances between trichomes
Trichomes (); ) are fine outgrowths or appendages on plants, algae, lichens, and certain protists. They are of diverse structure and function. Examples are hairs, glandular hairs, scales, and papillae. A covering of any kind of hair on a pla ...
and their patterning, which is a marker of the capability of a plant to resist to pathogenes.
Recently, the method is adapted as a support tool in the decision process underlying the selection, optimization, and management of financial portfolio
In finance, a portfolio is a collection of investments.
Definition
The term “portfolio” refers to any combination of financial assets such as stocks, bonds and cash. Portfolios may be held by individual investors or managed by financial p ...
s.
The method of elastic maps has been systematically tested and compared with several machine learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence.
Machine ...
methods on the applied problem of identification of the flow regime of a gas-liquid flow in a pipe. There are various regimes: Single phase water or air flow, Bubbly flow, Bubbly-slug flow, Slug flow, Slug-churn flow, Churn flow, Churn-annular flow, and Annular flow. The simplest and most common method used to identify the flow regime is visual observation. This approach is, however, subjective and unsuitable for relatively high gas and liquid flow rates. Therefore, the machine learning methods are proposed by many authors. The methods are applied to differential pressure data collected during a calibration process. The method of elastic maps provided a 2D map, where the area of each regime is represented. The comparison with some other machine learning methods is presented in Table 1 for various pipe diameters and pressure.
Here, ANN stands for the backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions gener ...
artificial neural network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains.
An ANN is based on a collection of connected units ...
s, SVM stands for the support vector machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories ...
, SOM for the self-organizing map
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional (typically two-dimensional) representation of a higher dimensional data set while preserving the ...
s. The hybrid technology was developed for engineering applications. In this technology, elastic maps are used in combination with Principal Component Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and ...
(PCA), Independent Component Analysis
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents. This is done by assuming that at most one subcomponent is Gaussian and that the subcomponents a ...
(ICA) and backpropagation ANN.
The textbookM. RestaComputational Intelligence Paradigms in Economic and Financial Decision Making
Series Intelligent Systems Reference Library, Volume 99, Springer International Publishing, Switzerland 2016. provides a systematic comparison of elastic maps and
self-organizing map
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised machine learning technique used to produce a low-dimensional (typically two-dimensional) representation of a higher dimensional data set while preserving the ...
s (SOMs) in applications to economic and financial decision-making.
References
{{reflist Data mining Dimension reduction