Distribution Fitting on:
[Wikipedia]
[Google]
[Amazon]
Probability distribution fitting or simply distribution fitting is the fitting of a
 The selection of the appropriate distribution depends on the presence or absence of symmetry of the data set with respect to the
The selection of the appropriate distribution depends on the presence or absence of symmetry of the data set with respect to the  When the larger values tend to be farther away from the mean than the smaller values, one has a skew distribution to the right (i.e. there is positive
When the larger values tend to be farther away from the mean than the smaller values, one has a skew distribution to the right (i.e. there is positive
/ref> the inverted (mirrored) Gumbel distribution, the
o
/ref> ::
/ref>
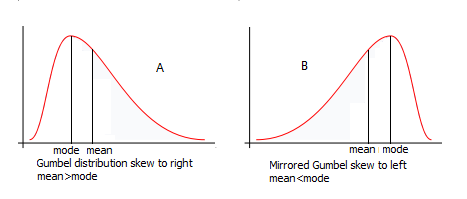 Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
The technique of distribution shifting augments the chance to find a properly fitting probability distribution.
 The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
 Predictions of occurrence based on fitted probability distributions are subject to
Predictions of occurrence based on fitted probability distributions are subject to 
probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon i ...
to a series of data concerning the repeated measurement of a variable phenomenon.
The aim of distribution fitting is to predict
A prediction (Latin ''præ-'', "before," and ''dicere'', "to say"), or forecast, is a statement about a future event or data. They are often, but not always, based upon experience or knowledge. There is no universal agreement about the exact ...
the probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ...
or to forecast the frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
of occurrence of the magnitude of the phenomenon in a certain interval.
There are many probability distributions (see list of probability distributions
Many probability distributions that are important in theory or applications have been given specific names.
Discrete distributions
With finite support
* The Bernoulli distribution, which takes value 1 with probability ''p'' and value 0 with pr ...
) of which some can be fitted more closely to the observed frequency of the data than others, depending on the characteristics of the phenomenon and of the distribution. The distribution giving a close fit is supposed to lead to good predictions.
In distribution fitting, therefore, one needs to select a distribution that suits the data well.
Selection of distribution
central tendency
In statistics, a central tendency (or measure of central tendency) is a central or typical value for a probability distribution.Weisberg H.F (1992) ''Central Tendency and Variability'', Sage University Paper Series on Quantitative Applications ...
.
''Symmetrical distributions''
When the data are symmetrically distributed around the mean while the frequency of occurrence of data farther away from the mean diminishes, one may for example select the normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
, the logistic distribution
Logistic may refer to:
Mathematics
* Logistic function, a sigmoid function used in many fields
** Logistic map, a recurrence relation that sometimes exhibits chaos
** Logistic regression, a statistical model using the logistic function
** Logit, ...
, or the Student's t-distribution
In probability and statistics, Student's ''t''-distribution (or simply the ''t''-distribution) is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in sit ...
. The first two are very similar, while the last, with one degree of freedom, has "heavier tails" meaning that the values farther away from the mean occur relatively more often (i.e. the kurtosis
In probability theory and statistics, kurtosis (from el, κυρτός, ''kyrtos'' or ''kurtos'', meaning "curved, arching") is a measure of the "tailedness" of the probability distribution of a real-valued random variable. Like skewness, kurtosi ...
is higher). The Cauchy distribution
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) fun ...
is also symmetric.
''Skew distributions to the right''
skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal d ...
), one may for example select the log-normal distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal ...
(i.e. the log values of the data are normally distributed), the log-logistic distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events ...
(i.e. the log values of the data follow a logistic distribution
Logistic may refer to:
Mathematics
* Logistic function, a sigmoid function used in many fields
** Logistic map, a recurrence relation that sometimes exhibits chaos
** Logistic regression, a statistical model using the logistic function
** Logit, ...
), the Gumbel distribution
In probability theory and statistics, the Gumbel distribution (also known as the type-I generalized extreme value distribution) is used to model the distribution of the maximum (or the minimum) of a number of samples of various distributions.
Thi ...
, the exponential distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average ...
, the Pareto distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto ( ), is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actua ...
, the Weibull distribution
In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Maurice Ren ...
, the Burr distribution
In probability theory, statistics and econometrics, the Burr Type XII distribution or simply the Burr distribution is a continuous probability distribution for a non-negative random variable. It is also known as the Singh–Maddala distribution a ...
, or the Fréchet distribution
The Fréchet distribution, also known as inverse Weibull distribution, is a special case of the generalized extreme value distribution. It has the cumulative distribution function
:\Pr(X \le x)=e^ \text x>0.
where ''α'' > 0 is a ...
. The last four distributions are bounded to the left.
''Skew distributions to the left''
When the smaller values tend to be farther away from the mean than the larger values, one has a skew distribution to the left (i.e. there is negative skewness), one may for example select the ''square-normal distribution'' (i.e. the normal distribution applied to the square of the data values),Left (negatively) skewed frequency histograms can be fitted to square Normal or mirrored Gumbel probability functions. On line/ref> the inverted (mirrored) Gumbel distribution, the
Dagum distribution
The Dagum distribution (or Mielke Beta-Kappa distribution) is a continuous probability distribution defined over positive real numbers. It is named after Camilo Dagum, who proposed it in a series of papers in the 1970s. The Dagum distribution aro ...
(mirrored Burr distribution), or the Gompertz distribution
In probability and statistics, the Gompertz distribution is a continuous probability distribution, named after Benjamin Gompertz. The Gompertz distribution is often applied to describe the distribution of adult lifespans by demographers and actu ...
, which is bounded to the left.
Techniques of fitting
The following techniques of distribution fitting exist: *''Parametric methods'', by which theparameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s of the distribution are calculated from the data series. The parametric methods are:
** Method of moments
**Maximum spacing estimation
In statistics, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model. The method requires maximization of the geometric mean of ''sp ...
**Method of L-moment
In statistics, L-moments are a sequence of statistics used to summarize the shape of a probability distribution. They are linear combinations of order statistics ( L-statistics) analogous to conventional moments, and can be used to calculate qu ...
s
**Maximum likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimation theory, estimating the Statistical parameter, parameters of an assumed probability distribution, given some observed data. This is achieved by Mathematical optimization, ...
method
::
*Plotting position
Plot or Plotting may refer to:
Art, media and entertainment
* Plot (narrative), the story of a piece of fiction
Music
* ''The Plot'' (album), a 1976 album by jazz trumpeter Enrico Rava
* The Plot (band), a band formed in 2003
Other
* ''Plot'' ...
plus Regression analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one ...
, using a transformation of the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
so that a linear relation
In linear algebra, a linear relation, or simply relation, between elements of a vector space or a module is a linear equation that has these elements as a solution.
More precisely, if e_1,\dots,e_n are elements of a (left) module over a ring ( ...
is found between the cumulative probability
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
and the values of the data, which may also need to be transformed, depending on the selected probability distribution. In this method the cumulative probability needs to be estimated by the plotting position
Plot or Plotting may refer to:
Art, media and entertainment
* Plot (narrative), the story of a piece of fiction
Music
* ''The Plot'' (album), a 1976 album by jazz trumpeter Enrico Rava
* The Plot (band), a band formed in 2003
Other
* ''Plot'' ...
Software for Generalized and Composite Probability Distributions. International Journal of Mathematical and Computational Methods, 4, 1-o
/ref> ::
Generalization of distributions
It is customary to transform data logarithmically to fit symmetrical distributions (like the normal distribution, normal and logistic) to data obeying a distribution that is positively skewed (i.e. skew to the right, withmean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.
For a data set, the ''arithme ...
> mode
Mode ( la, modus meaning "manner, tune, measure, due measure, rhythm, melody") may refer to:
Arts and entertainment
* '' MO''D''E (magazine)'', a defunct U.S. women's fashion magazine
* ''Mode'' magazine, a fictional fashion magazine which is ...
, and with a right hand tail that is longer than the left hand tail), see lognormal distribution
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable is log-normally distributed, then has a normal ...
and the loglogistic distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events ...
. A similar effect can be achieved by taking the square root of the data.
To fit a symmetrical distribution to data obeying a negatively skewed distribution (i.e. skewed to the left, with mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.
For a data set, the ''arithme ...
< mode
Mode ( la, modus meaning "manner, tune, measure, due measure, rhythm, melody") may refer to:
Arts and entertainment
* '' MO''D''E (magazine)'', a defunct U.S. women's fashion magazine
* ''Mode'' magazine, a fictional fashion magazine which is ...
, and with a right hand tail this is shorter than the left hand tail) one could use the squared values of the data to accomplish the fit.
More generally one can raise the data to a power ''p'' in order to fit symmetrical distributions to data obeying a distribution of any skewness, whereby ''p'' < 1 when the skewness is positive and ''p'' > 1 when the skewness is negative. The optimal value of ''p'' is to be found by a numerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
. The numerical method may consist of assuming a range of ''p'' values, then applying the distribution fitting procedure repeatedly for all the assumed ''p'' values, and finally selecting the value of ''p'' for which the sum of squares of deviations of calculated probabilities from measured frequencies ( chi squared) is minimum, as is done in CumFreq
In statistics and data analysis the application software CumFreq is a tool for cumulative frequency analysis of a single variable and for probability distribution fitting.
Originally the method was developed for the analysis of hydrological ...
.
The generalization enhances the flexibility of probability distributions and increases their applicability in distribution fitting.
The versatility of generalization makes it possible, for example, to fit approximately normally distributed data sets to a large number of different probability distributions, while negatively skewed distributions can be fitted to
square normal and mirrored Gumbel distributions.Left (negatively) skewed frequency histograms can be
fitted to square normal or mirrored Gumbel probability functions/ref>
Inversion of skewness
 Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(F) by its complement: F'=1-F, obtaining the Cumulative distribution function#Complementary cumulative distribution function (tail distribution), complementary distribution function (also called survival function
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive past a certain time.
The survival function is also known as the survivor function
or reliability function.
The term ...
) that gives a mirror image. In this manner, a distribution that is skewed to the right is transformed into a distribution that is skewed to the left and vice versa.
::
The technique of skewness inversion increases the number of probability distributions available for distribution fitting and enlarges the distribution fitting opportunities.
Shifting of distributions
Some probability distributions, like theexponential
Exponential may refer to any of several mathematical topics related to exponentiation, including:
*Exponential function, also:
**Matrix exponential, the matrix analogue to the above
* Exponential decay, decrease at a rate proportional to value
*Exp ...
, do not support data values (''X'') equal to or less than zero. Yet, when negative data are present, such distributions can still be used replacing ''X'' by ''Y''=''X''-''Xm'', where ''Xm'' is the minimum value of ''X''. This replacement represents a shift of the probability distribution in positive direction, i.e. to the right, because ''Xm'' is negative. After completing the distribution fitting of ''Y'', the corresponding ''X''-values are found from ''X''=''Y''+''Xm'', which represents a back-shift of the distribution in negative direction, i.e. to the left.The technique of distribution shifting augments the chance to find a properly fitting probability distribution.
Composite distributions
 The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the Laplace distribution
In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponen ...
. The ranges are separated by a break-point. The use of such composite (discontinuous) probability distributions can be opportune when the data of the phenomenon studied were obtained under two sets different conditions.
Uncertainty of prediction
 Predictions of occurrence based on fitted probability distributions are subject to
Predictions of occurrence based on fitted probability distributions are subject to uncertainty
Uncertainty refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or ...
, which arises from the following conditions:
* The true probability distribution of events may deviate from the fitted distribution, as the observed data series may not be totally representative of the real probability of occurrence of the phenomenon due to random error
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. In statistics, an error is not necessarily a " mistake ...
* The occurrence of events in another situation or in the future may deviate from the fitted distribution as this occurrence can also be subject to random error
* A change of environmental conditions may cause a change in the probability of occurrence of the phenomenon
An estimate of the uncertainty in the first and second case can be obtained with the binomial probability distribution using for example the probability of exceedance ''Pe'' (i.e. the chance that the event ''X'' is larger than a reference value ''Xr'' of ''X'') and the probability of non-exceedance ''Pn'' (i.e. the chance that the event ''X'' is smaller than or equal to the reference value ''Xr'', this is also called cumulative probability
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
). In this case there are only two possibilities: either there is exceedance or there is non-exceedance. This duality is the reason that the binomial distribution is applicable.
With the binomial distribution one can obtain a prediction interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are o ...
. Such an interval also estimates the risk of failure, i.e. the chance that the predicted event still remains outside the confidence interval. The confidence or risk analysis may include the return period A return period, also known as a recurrence interval or repeat interval, is an average time or an estimated average time between events such as earthquakes, floods, landslides, or river discharge flows to occur.
It is a statistical measurement typ ...
''T=1/Pe'' as is done in hydrology
Hydrology () is the scientific study of the movement, distribution, and management of water on Earth and other planets, including the water cycle, water resources, and environmental watershed sustainability. A practitioner of hydrology is calle ...
.

Goodness of fit
By ranking thegoodness of fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measure ...
of various distributions one can get an impression of which distribution is acceptable and which is not.
Histogram and density function
From thecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(CDF) one can derive a histogram
A histogram is an approximate representation of the distribution of numerical data. The term was first introduced by Karl Pearson. To construct a histogram, the first step is to " bin" (or "bucket") the range of values—that is, divide the ent ...
and the probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can ...
(PDF).
See also
*Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is ...
* Density estimation
In statistics, probability density estimation or simply density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function. The unobservable density function is thought o ...
* Mixture distribution
In probability and statistics, a mixture distribution is the probability distribution of a random variable that is derived from a collection of other random variables as follows: first, a random variable is selected by chance from the collection a ...
* Product distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables ''X'' and ''Y'', the distribution of ...
References
{{Distribution fitting software