discontinuous

Continuous functions are of utmost importance in mathematics, functions and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set, or even the entire domain of the function. This article describes the classification of discontinuities in the simplest case of functions of a single real variable taking real values.

The oscillation of a function at a point quantifies these discontinuities as follows:
* in a removable discontinuity, the distance that the value of the function is off by is the oscillation;
* in a jump discontinuity, the size of the jump is the oscillation (assuming that the value ''at'' the point lies between these limits of the two sides);
* in an essential discontinuity, oscillation measures the failure of a limit to exist; the limit is constant.
A special case is if the function diverges to infinity or minus infinity, in which case the oscillation is not defined (in the extended real numbers, this is a removable discontinuity).

Classification

For each of the following, consider a real valued function $f$ of a real variable $x,$ defined in a neighborhood of the point $x_0$ at which $f$ is discontinuous.

Removable discontinuity

Consider the piecewise function
$f(x) = \begin x^2 & \text x < 1 \\ 0 & \text x = 1 \\ 2-x & \text x > 1 \end$

The point $x_0 = 1$ is a ''removable discontinuity''. For this kind of discontinuity:

The one-sided limit from the negative direction:
$L^- = \lim_ f(x)$
and the one-sided limit from the positive direction:
$L^+ = \lim_ f(x)$
at $x_0$ ''both'' exist, are finite, and are equal to $L = L^- = L^+.$ In other words, since the two one-sided limits exist and are equal, the limit $L$ of $f(x)$ as $x$ approaches $x_0$ exists and is equal to this same value. If the actual value of $f\left(x_0\right)$ is ''not'' equal to $L,$ then $x_0$ is called a . This discontinuity can be removed to make $f$ continuous at $x_0,$ or more precisely, the function
$g(x) = \begin f(x) & x \neq x_0 \\ L & x = x_0 \end$
is continuous at $x = x_0.$

The term ''removable discontinuity'' is sometimes broadened to include a removable singularity, in which the limits in both directions exist and are equal, while the function is undefined at the point $x_0.$ This use is an abuse of terminology because continuity and discontinuity of a function are concepts defined only for points in the function's domain.

Jump discontinuity

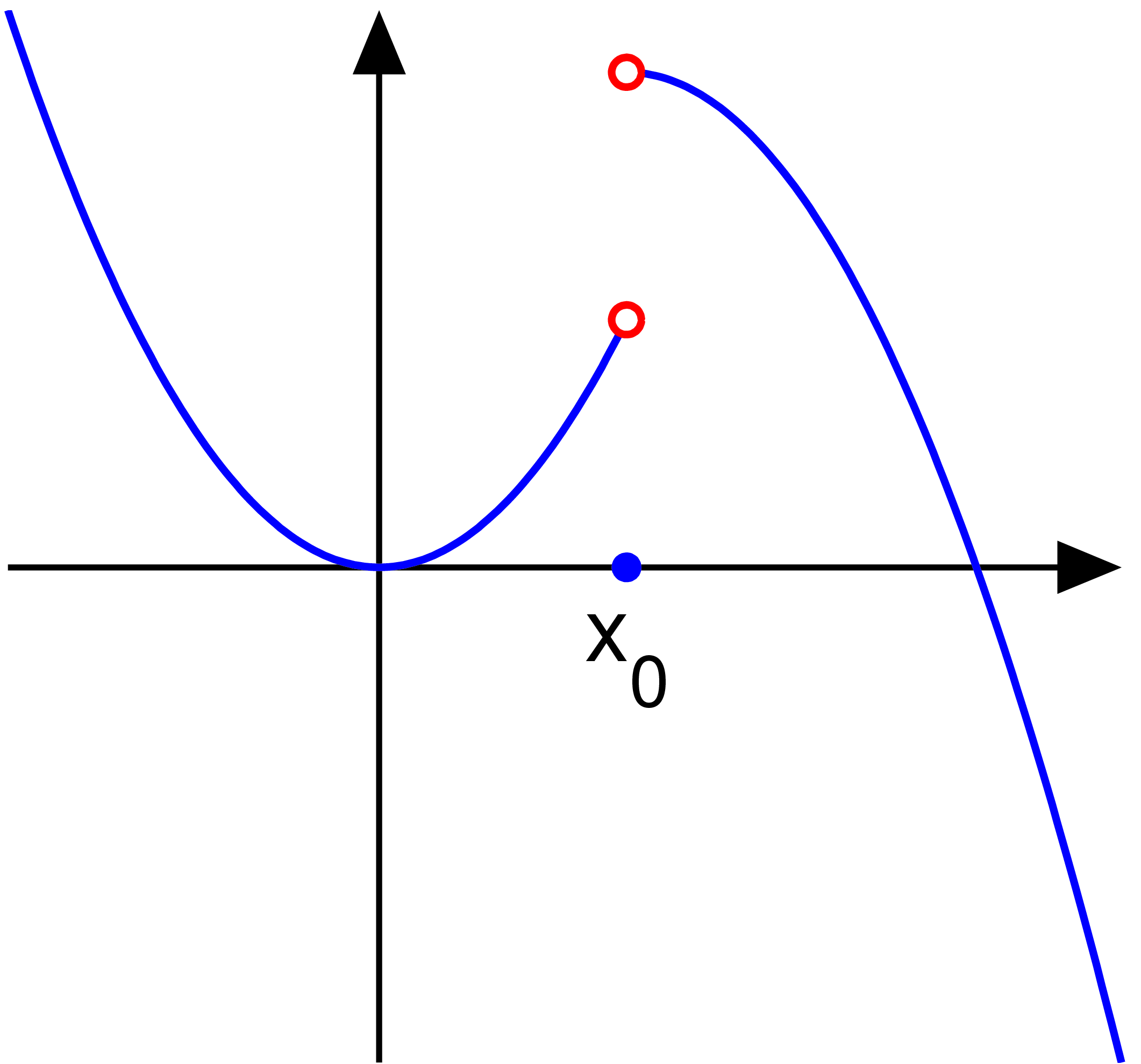
Consider the function
$f(x) = \begin x^2 & \mbox x < 1 \\ 0 & \mbox x = 1 \\ 2 - (x-1)^2 & \mbox x > 1 \end$

Then, the point $x_0 = 1$ is a '.

In this case, a single limit does not exist because the one-sided limits, $L^-$ and $L^+$ exist and are finite, but are not equal: since, $L^- \neq L^+,$ the limit $L$ does not exist. Then, $x_0$ is called a ''jump discontinuity'', ''step discontinuity'', or ''discontinuity of the first kind''. For this type of discontinuity, the function $f$ may have any value at $x_0.$

Essential discontinuity

For an essential discontinuity, at least one of the two one-sided limits does not exist in $\mathbb$. (Notice that one or both one-sided limits can be $\pm\infty$).

Consider the function
$f(x) = \begin \sin\frac & \text x < 1 \\ 0 & \text x = 1 \\ \frac & \text x > 1. \end$

Then, the point $x_0 = 1$ is an '.

In this example, both $L^-$ and $L^+$ do not exist in $\mathbb$, thus satisfying the condition of essential discontinuity. So $x_0$ is an essential discontinuity, infinite discontinuity, or discontinuity of the second kind. (This is distinct from an essential singularity, which is often used when studying functions of complex variables).

Supposing that $f$ is a function defined on an interval $I \subseteq \R,$ we will denote by $D$ the set of all discontinuities of $f$ on $I.$ By $R$ we will mean the set of all $x_0\in I$ such that $f$ has a ''removable'' discontinuity at $x_0.$ Analogously by $J$ we denote the set constituted by all $x_0\in I$ such that $f$ has a ''jump'' discontinuity at $x_0.$ The set of all $x_0\in I$ such that $f$ has an ''essential'' discontinuity at $x_0$ will be denoted by $E.$ Of course then $D = R \cup J \cup E.$

Counting discontinuities of a function

The two following properties of the set $D$ are relevant in the literature.

* The set of $D$ is an $F_$ set. The set of points at which a function is continuous is always a $G_$ set (see).

* If on the interval $I,$ $f$ is monotone then $D$ is at most countable and $D = J.$ This is Froda's theorem.
Tom Apostol follows partially the classification above by considering only removal and jump discontinuities. His objective is to study the discontinuities of monotone functions, mainly to prove Froda’s theorem. With the same purpose, Walter Rudin and Karl R. Stromberg study also removal and jump discontinuities by using different terminologies. However, furtherly, both authors state that $R \cup J$ is always a countable set (see).

The term essential discontinuity seems to have been introduced by John Klippert. Furtherly he also classified essential discontinuities themselves by subdividing the set $E$ into the three following sets:

$E_1 = \left\,$
$E_2 = \left\,$
$E_3 = \left\.$

Of course $E=E_1 \cup E_2 \cup E_3.$ Whenever $x_0\in E_1,$ $x_0$ is called an ''essential discontinuity of first kind''. Any $x_0 \in E_2 \cup E_3$ is said an ''essential discontinuity of second kind.'' Hence he enlarges the set $R \cup J$ without losing its characteristic of being countable, by stating the following:

* The set $R \cup J \cup E_2 \cup E_3$ is countable.

Rewriting Lebesgue's Theorem

When I= ,b/math> and $f$ is a bounded function, it is well-known of the importance of the set $D$ in the regard of the Riemann integrability of $f.$ In fact, Lebesgue's Theorem (also named Lebesgue-Vitali) theorem) states that $f$ is Riemann integrable on I = ,b/math> if and only if $D$ is a set with Lebesgue's measure zero.

In this theorem seems that all type of discontinuities have the same weight on the obstruction that a bounded function $f$ be Riemann integrable on ,b Since countable sets are sets of Lebesgue's measure zero and a countable union of sets with Lebesgue's measure zero is still a set of Lebesgue's mesure zero, we are seeing now that this is not the case. In fact, the discontinuities in the set $R \cup J \cup E_2 \cup E_3$ are absolutly neutral in the regard of the Riemann integrability of $f.$ The main discontinuities for that purpose are the essential discontinuities of first kind and consequently the Lebesgue-Vitali theorem can be rewritten as follows:

* A bounded function, $f,$ is Riemann integrable on ,b/math> if and only if the correspondent set $E_1$ of all essential discontinuities of first kind of $f$ has Lebesgue's measure zero.

The case where $E_1 = \varnothing$ correspond to the following well-known classical complementary situations of Riemann integrability of a bounded function $f :$, b\to \R:

* If $f$ has right-hand limit at each point of , b[ then $f$ is Riemann integrable on [a, b/math> (see)
* If $f$ has left-hand limit at each point of $]a, b]$ then $f$ is Riemann integrable on $$, b
* If $f$ is a regulated function on $$, b/math> then $f$ is Riemann integrable on $$, b

Examples

Thomae's function is discontinuous at every non-zero rational point, but continuous at every irrational point. One easily sees that those discontinuities are all essential of the first kind, that is $E_1 = \Q.$ By the first paragraph, there does not exist a function that is continuous at every rational point, but discontinuous at every irrational point.

The indicator function of the rationals, also known as the Dirichlet function, is discontinuous everywhere. These discontinuities are all essential of the first kind too.

Consider now the ternary Cantor set \mathcal \subset ,1/math> and its indicator (or characteristic) function
\mathbf 1_\mathcal(x) = \begin
1 & x \in \mathcal \\
0 & x \notin ,1\setminus \mathcal.
\end
One way to construct the Cantor set $\mathcal$ is given by $\mathcal := \bigcap_^\infty C_n$ where the sets $C_n$ are obtained by recurrence according to
$C_n = \frac 3 \cup \left(\frac 2 + \frac 3\right) \text n \geq 1, \text C_0 =$, 1

In view of the discontinuities of the function $\mathbf 1_\mathcal(x),$ let's assume a point $x_0\not\in\mathcal.$

Therefore there exists a set $C_n,$ used in the formulation of $\mathcal$, which does not contain $x_0.$ That is, $x_0$ belongs to one of the open intervals which were removed in the construction of $C_n.$ This way, $x_0$ has a neighbourhood with no points of $\mathcal.$ (In another way, the same conclusion follows taking into account that $\mathcal$ is a closed set and so its complementary with respect to $$, 1/math> is open). Therefore $\mathbf 1_\mathcal$ only assumes the value zero in some neighbourhood of $x_0.$ Hence $\mathbf 1_\mathcal$ is continuous at $x_0.$

This means that the set $D$ of all discontinuities of $\mathbf 1_\mathcal$ on the interval $$, 1/math> is a subset of $\mathcal.$ Since $\mathcal$ is a noncountable set with null Lebesgue measure, also $D$ is a null Lebesgue measure set and so in the regard of Lebesgue-Vitali theorem $\mathbf 1_\mathcal$ is a Riemann integrable function.

More precisely one has $D = \mathcal.$ In fact, since $\mathcal$ is a rare (closed of empty interior) set, if $x_0\in\mathcal$ then no neighbourhood $\left(x_0-\varepsilon, x_0+\varepsilon\right)$ of $x_0,$ can be contained in $\mathcal.$ This way, any neighbourhood of $x_0\in\mathcal$ contains points of $\mathcal$ and points which are not of $\mathcal.$ In terms of the function $\mathbf 1_\mathcal$ this means that both $\lim_ \mathbf 1_\mathcal(x)$ and $\lim_ 1_\mathcal(x)$ do not exist. That is, $D = E_1,$ where by $E_1,$ as before, we denote the set of all essential discontinuities of first kind of the function $\mathbf 1_\mathcal.$ Clearly $\int_0^1 \mathbf 1_\mathcal(x)dx = 0.$

Discontinuities of derivatives

Let now $I \subseteq \R$ an open interval and$f:I\to\mathbb$ the derivative of a function, $F:I\to\mathbb$, differentiable on $I$. That is, $F'(x)=f(x)$ for every $x\in I$.

It is well-known that according to Darboux's Theorem the derivative function $f: I \to \Reals$ has the restriction of satisfying the intermediate value property.

$f$ can of course be continuous on the interval $I$. Recall that any continuous function, by Bolzano's Theorem, satisfies the intermediate value property.

On the other hand, the intermediate value property does not prevent $f$ from having discontinuities on the interval $I$. But Darboux's Theorem has an immediate consequence on the type of discontinuities that $f$ can have. In fact, if $x_0\in I$ is a point of discontinuity of $f$, then necessarily $x_0$ is an essential discontinuity of $f$.

This means in particular that the following two situations cannot occur:

Furtherly, two other situations have to be excluded (see John Klippert):

Observe that whenever one of the conditions (i), (ii), (iii), or (iv) is fulfilled for some $x_0\in I$ one can conclude that $f$ fails to possess an antiderivative, $F$, on the interval $I$.

On the other hand, a new type of discontinuity with respect to any function $f:I\to\mathbb$ can be introduced: an essential discontinuity, $x_0 \in I$, of the function $f$, is said to be a ''fundamental essential discontinuity'' of $f$ if

$\lim_ f(x)\neq\pm\infty$ and $\lim_ f(x)\neq\pm\infty.$

Therefore if $x_0\in I$ is a discontinuity of a derivative function $f:I\to\mathbb$, then necessarily $x_0$ is a fundamental essential discontinuity of $f$.

Notice also that when I= ,b/math> and $f:I\to\mathbb$ is a bounded function, as in the assumptions of Lebesgue's Theorem, we have for all $x_0\in (a,b)$:
$\lim_ f(x)\neq\pm\infty ,$
$\lim_ f(x)\neq\pm\infty,$ and
$\lim_ f(x)\neq\pm\infty.$
Therefore any essential discontinuity of $f$ is a fundamental one.

See also

*
*
*
*
**
**

Notes

References

Sources

*

External links

*

"Discontinuity"
by Ed Pegg, Jr., The Wolfram Demonstrations Project, 2007.
*
* {{SpringerEOM, title=Discontinuity point , id=Discontinuity_point , oldid=12112 , first=L.D. , last=Kudryavtsev, mode=cs1

Theory of continuous functions
Mathematical analysis
Mathematical classification systems