Cantor Function on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 To define the Cantor function (precisely, it is
To define the Cantor function (precisely, it is c(x)=\mu( ,x . This probability distribution, called the
\sum\limits_^M (y_k-x_k)<\delta and \sum\limits_^M (c(y_k)-c(x_k))=1 .
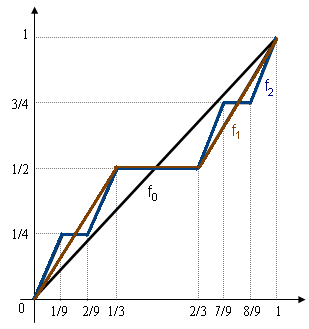 Below we define a sequence of functions on the unit interval that converges to the Cantor function.
Let ''f''0(''x'') = ''x''.
Then, for every integer , the next function ''f''''n''+1(''x'') will be defined in terms of ''f''''n''(''x'') as follows:
Let ''f''''n''+1(''x'') = , when ;
Let ''f''''n''+1(''x'') = 1/2, when ;
Let ''f''''n''+1(''x'') = , when .
The three definitions are compatible at the end-points 1/3 and 2/3, because ''f''''n''(0) = 0 and ''f''''n''(1) = 1 for every ''n'', by induction. One may check that ''f''''n'' converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ''f''''n''+1, one sees that
:
Below we define a sequence of functions on the unit interval that converges to the Cantor function.
Let ''f''0(''x'') = ''x''.
Then, for every integer , the next function ''f''''n''+1(''x'') will be defined in terms of ''f''''n''(''x'') as follows:
Let ''f''''n''+1(''x'') = , when ;
Let ''f''''n''+1(''x'') = 1/2, when ;
Let ''f''''n''+1(''x'') = , when .
The three definitions are compatible at the end-points 1/3 and 2/3, because ''f''''n''(0) = 0 and ''f''''n''(1) = 1 for every ''n'', by induction. One may check that ''f''''n'' converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ''f''''n''+1, one sees that
:\max_ , f_(x) - f_n(x), \le \frac 1 2 \, \max_ , f_(x) - f_(x), , \quad n \ge 1.
If ''f'' denotes the limit function, it follows that, for every ''n'' ≥ 0,
:\max_ , f(x) - f_n(x), \le 2^ \, \max_ , f_1(x) - f_0(x), .
Also the choice of starting function does not really matter, provided ''f''0(0) = 0, ''f''0(1) = 1 and ''f''0 is bounded.
\ldots can be replaced by 0222\ldots to get rid of any 1). It turns out that the Cantor set is a H_D (in the sense of a Hausdorff-measure) takes a finite value, where D = \log(2)/\log(3) is the fractal dimension of ''C''. We may define the Cantor function alternatively as the ''D''-dimensional volume of sections of the Cantor set
:
f(x)=H_D(C \cap (0,x)).
0\le x\le 1 , there is a reflection symmetry
:c(x)=1-c(1-x)
and a pair of magnifications, one on the left and one on the right:
:c\left(\frac\right) = \frac
and
:c\left(\frac\right) = \frac
The magnifications can be cascaded; they generate the r(x)=1-x
The first self-symmetry can be expressed as
:r\circ c = c\circ r
where the symbol \circ denotes function composition. That is, (r\circ c)(x)=r(c(x))=1-c(x) and likewise for the other cases. For the left and right magnifications, write the left-mappings
:L_D(x)= \frac and L_C(x)= \frac
Then the Cantor function obeys
:L_D \circ c = c \circ L_C
Similarly, define the right mappings as
:R_D(x)= \frac and R_C(x)= \frac
Then, likewise,
:R_D \circ c = c \circ R_C
The two sides can be mirrored one onto the other, in that
:L_D \circ r = r\circ R_D
and likewise,
:L_C \circ r = r\circ R_C
These operations can be stacked arbitrarily. Consider, for example, the sequence of left-right moves LRLLR. Adding the subscripts C and D, and, for clarity, dropping the composition operator \circ in all but a few places, one has:
:L_D R_D L_D L_D R_D \circ c = c \circ L_C R_C L_C L_C R_C
Arbitrary finite-length strings in the letters L and R correspond to the dyadic rationals, in that every dyadic rational can be written as both y=n/2^m for integer ''n'' and ''m'' and as finite length of bits y=0.b_1b_2b_3\cdots b_m with b_k\in \. Thus, every dyadic rational is in one-to-one correspondence with some self-symmetry of the Cantor function.
Some notational rearrangements can make the above slightly easier to express. Let g_0 and g_1 stand for L and R. Function composition extends this to a g_=g_0g_1g_0 and generally, g_Ag_B=g_ for some binary strings of digits ''A'', ''B'', where ''AB'' is just the ordinary \gamma\in M as a general element of the monoid, there is a corresponding self-symmetry of the Cantor function:
:\gamma_D\circ c= c\circ \gamma_C
The dyadic monoid itself has several interesting properties. It can be viewed as a finite number of left-right moves down an infinite SL(2,\mathbb).
Note that the Cantor function bears more than a passing resemblance to Minkowski's question-mark function. In particular, it obeys the exact same symmetry relations, although in an altered form.
y=\sum_^\infty b_k 2^
be the dyadic (binary) expansion of the real number 0 ≤ ''y'' ≤ 1 in terms of binary digits ''b''''k'' ∈ . This expansion is discussed in greater detail in the article on the C_z(y)=\sum_^\infty b_k z^.
For ''z'' = 1/3, the inverse of the function ''x'' = 2 ''C''1/3(''y'') is the Cantor function. That is, ''y'' = ''y''(''x'') is the Cantor function. In general, for any ''z'' < 1/2, ''C''''z''(''y'') looks like the Cantor function turned on its side, with the width of the steps getting wider as ''z'' approaches zero.
As mentioned above, the Cantor function is also the cumulative distribution function of a measure on the Cantor set. Different Cantor functions, or Devil's Staircases, can be obtained by considering different atom-less probability measures supported on the Cantor set or other fractals. While the Cantor function has derivative 0 almost everywhere, current research focusses on the question of the size of the set of points where the upper right derivative is distinct from the lower right derivative, causing the derivative to not exist. This analysis of differentiability is usually given in terms of fractal dimension, with the Hausdorff dimension the most popular choice. This line of research was started in the 1990s by Darst, who showed that the Hausdorff dimension of the set of non-differentiability of the Cantor function is the square of the dimension of the Cantor set, (\log2/\log3)^2 . Subsequently Falconer showed that this squaring relationship holds for all Ahlfor's regular, singular measures, i.e.\dim_H\left\=\left(\dim_H\operatorname(\mu)\right)^2 Later, Troscheit obtain a more comprehensive picture of the set where the derivative does not exist for more general normalized Gibb's measures supported on self-conformal and self-similar sets.
''Cantor ternary function'' at Encyclopaedia of Mathematics
Cantor Function
by Douglas Rivers, the Wolfram Demonstrations Project. * {{fractals, state=collapsed Fractals Measure theory Special functions Georg Cantor De Rham curves
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the Cantor function is an example of a function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-oriente ...
that is continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
, but not absolutely continuous
In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central ope ...
. It is a notorious counterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "John Smith is not a lazy student" is a ...
in analysis, because it challenges naive intuitions about continuity, derivative, and measure. Though it is continuous everywhere and has zero derivative almost everywhere, its value still goes from 0 to 1 as its argument reaches from 0 to 1. Thus, in one sense the function seems very much like a constant one which cannot grow, and in another, it does indeed monotonically grow.
It is also called the Cantor ternary function, the Lebesgue function, Lebesgue's singular function, the Cantor–Vitali function, the Devil's staircase, the Cantor staircase function, and the Cantor–Lebesgue function. introduced the Cantor function and mentioned that Scheeffer pointed out that it was a counterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "John Smith is not a lazy student" is a ...
to an extension of the fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at each time) with the concept of integrating a function (calculating the area under its graph, or ...
claimed by Harnack Harnack is the surname of a German family of intellectuals, artists, mathematicians, scientists, theologians and those in other fields. Several family members were executed by the Nazis during the last years of the Third Reich.
* Theodosius Harnac ...
. The Cantor function was discussed and popularized by , and .
Definition
 To define the Cantor function
To define the Cantor function Hölder continuous Hölder:
* ''Hölder, Hoelder'' as surname
* Hölder condition
* Hölder's inequality
* Hölder mean
In mathematics, generalized means (or power mean or Hölder mean from Otto Hölder) are a family of functions for aggregating sets of number ...
of exponent ''α'' = log 2/log 3) but not absolutely continuous
In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central ope ...
. It is constant on intervals of the form (0.''x''1''x''2''x''3...''x''n022222..., 0.''x''1''x''2''x''3...''x''n200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
at any point in an uncountable
In mathematics, an uncountable set (or uncountably infinite set) is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal num ...
subset of the Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
Thr ...
containing the interval endpoints described above.
The Cantor function can also be seen as the cumulative probability distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
of the 1/2-1/2 Bernoulli measure
In probability and statistics, a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The ...
''μ'' supported on the Cantor set: Cantor distribution
The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function.
This distribution has neither a probability density function nor a probability mass function, since although its cumulativ ...
, has no discrete part. That is, the corresponding measure is atomless. This is why there are no jump discontinuities in the function; any such jump would correspond to an atom in the measure.
However, no non-constant part of the Cantor function can be represented as an integral of a probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can ...
; integrating any putative probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can ...
that is not almost everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to ...
zero over any interval will give positive probability to some interval to which this distribution assigns probability zero. In particular, as pointed out, the function is not the integral of its derivative even though the derivative exists almost everywhere.
The Cantor function is the standard example of a singular function
In mathematics, a real-valued function ''f'' on the interval 'a'', ''b''is said to be singular if it has the following properties:
*''f'' is continuous on 'a'', ''b'' (**)
*there exists a set ''N'' of measure 0 such that for all ''x'' outside ...
.
The Cantor function is non-decreasing, and so in particular its graph defines a rectifiable curve. showed that the arc length of its graph is 2.
Lack of absolute continuity
Because the Lebesgue measure of theuncountably infinite
In mathematics, an uncountable set (or uncountably infinite set) is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal num ...
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
Thr ...
is 0, for any positive ''ε'' < 1 and ''δ'', there exists a finite sequence of pairwise disjoint
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A c ...
sub-intervals with total length < ''δ'' over which the Cantor function cumulatively rises more than ''ε''.
In fact, for every ''δ'' > 0 there are finitely many pairwise disjoint intervals (''xk'',''yk'') (1 ≤ ''k'' ≤ ''M'') with Alternative definitions
Iterative construction
 Below we define a sequence of functions on the unit interval that converges to the Cantor function.
Let ''f''0(''x'') = ''x''.
Then, for every integer , the next function ''f''''n''+1(''x'') will be defined in terms of ''f''''n''(''x'') as follows:
Let ''f''''n''+1(''x'') = , when ;
Let ''f''''n''+1(''x'') = 1/2, when ;
Let ''f''''n''+1(''x'') = , when .
The three definitions are compatible at the end-points 1/3 and 2/3, because ''f''''n''(0) = 0 and ''f''''n''(1) = 1 for every ''n'', by induction. One may check that ''f''''n'' converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ''f''''n''+1, one sees that
:
Below we define a sequence of functions on the unit interval that converges to the Cantor function.
Let ''f''0(''x'') = ''x''.
Then, for every integer , the next function ''f''''n''+1(''x'') will be defined in terms of ''f''''n''(''x'') as follows:
Let ''f''''n''+1(''x'') = , when ;
Let ''f''''n''+1(''x'') = 1/2, when ;
Let ''f''''n''+1(''x'') = , when .
The three definitions are compatible at the end-points 1/3 and 2/3, because ''f''''n''(0) = 0 and ''f''''n''(1) = 1 for every ''n'', by induction. One may check that ''f''''n'' converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ''f''''n''+1, one sees that
:Fractal volume
The Cantor function is closely related to theCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
Thr ...
. The Cantor set ''C'' can be defined as the set of those numbers in the interval , 1that do not contain the digit 1 in their base-3 (triadic) expansion, except if the 1 is followed by zeros only (in which case the tail 1000fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
with (uncountably) infinitely many points (zero-dimensional volume), but zero length (one-dimensional volume). Only the ''D''-dimensional volume Self-similarity
The Cantor function possesses severalsymmetries
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
. For dyadic monoid
In mathematics, the modular group is the projective special linear group of matrices with integer coefficients and determinant 1. The matrices and are identified. The modular group acts on the upper-half of the complex plane by fractiona ...
. This is exhibited by defining several helper functions. Define the reflection as
:monoid
In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0.
Monoids ...
, in that one can write concatenation
In formal language theory and computer programming, string concatenation is the operation of joining character strings end-to-end. For example, the concatenation of "snow" and "ball" is "snowball". In certain formalisations of concatenat ...
of such strings. The dyadic monoid ''M'' is then the monoid of all such finite-length left-right moves. Writing binary tree
In computer science, a binary tree is a k-ary k = 2 tree data structure in which each node has at most two children, which are referred to as the ' and the '. A recursive definition using just set theory notions is that a (non-empty) binary t ...
; the infinitely distant "leaves" on the tree correspond to the points on the Cantor set, and so, the monoid also represents the self-symmetries of the Cantor set. In fact, a large class of commonly occurring fractals are described by the dyadic monoid; additional examples can be found in the article on de Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.
The Cantor function, Cesàro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve, and Koch curve are all spe ...
s. Other fractals possessing self-similarity are described with other kinds of monoids. The dyadic monoid is itself a sub-monoid of the modular group Generalizations
Let :dyadic transformation
The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation)
: T: , 1) \to [0, 1)^\infty
: x \mapsto (x_0, x_1, x_2, ...
. Then consider the function
: Hermann Minkowski
Hermann Minkowski (; ; 22 June 1864 – 12 January 1909) was a German mathematician and professor at Königsberg, Zürich and Göttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in number t ...
's question mark function loosely resembles the Cantor function visually, appearing as a "smoothed out" form of the latter; it can be constructed by passing from a continued fraction expansion to a binary expansion, just as the Cantor function can be constructed by passing from a ternary expansion to a binary expansion. The question mark function has the interesting property of having vanishing derivatives at all rational numbers.
See also
*Dyadic transformation
The dyadic transformation (also known as the dyadic map, bit shift map, 2''x'' mod 1 map, Bernoulli map, doubling map or sawtooth map) is the mapping (i.e., recurrence relation)
: T: , 1) \to [0, 1)^\infty
: x \mapsto (x_0, x_1, x_2, ...
Notes
References
* * Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980. * * * * * * * * *External links
''Cantor ternary function'' at Encyclopaedia of Mathematics
Cantor Function
by Douglas Rivers, the Wolfram Demonstrations Project. * {{fractals, state=collapsed Fractals Measure theory Special functions Georg Cantor De Rham curves