cross-validation (statistics)

Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set.
Cross-validation is a resampling method that uses different portions of the data to test and train a model on different iterations. It is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. In a prediction problem, a model is usually given a dataset of ''known data'' on which training is run (''training dataset''), and a dataset of ''unknown data'' (or ''first seen'' data) against which the model is tested (called the validation dataset or ''testing set''). The goal of cross-validation is to test the model's ability to predict new data that was not used in estimating it, in order to flag problems like overfitting or selection bias and to give an insight on how the model will generalize to an independent dataset (i.e., an unknown dataset, for instance from a real problem).

One round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset (called the ''training set''), and validating the analysis on the other subset (called the ''validation set'' or ''testing set''). To reduce variability, in most methods multiple rounds of cross-validation are performed using different partitions, and the validation results are combined (e.g. averaged) over the rounds to give an estimate of the model's predictive performance.

In summary, cross-validation combines (averages) measures of fitness in prediction to derive a more accurate estimate of model prediction performance.

Motivation

Assume a model with one or more unknown parameters, and a data set to which the model can be fit (the training data set). The fitting process optimizes the model parameters to make the model fit the training data as well as possible. If an independent sample of validation data is taken from the same population as the training data, it will generally turn out that the model does not fit the validation data as well as it fits the training data. The size of this difference is likely to be large especially when the size of the training data set is small, or when the number of parameters in the model is large. Cross-validation is a way to estimate the size of this effect.

In linear regression, there exist real ''response values'' ''y''₁, ..., ''y_n'', and ''n'' ''p''-dimensional vector ''covariates'' ''x''₁, ..., ''x''_''n''. The components of the vector ''x''_''i'' are denoted ''x''_''i''1, ..., ''x''_''ip''. If least squares is used to fit a function in the form of a hyperplane ''ŷ'' = ''a'' + ''β''^T''x'' to the data (''x''_''i'', ''y''_''i'') _{1 ≤ ''i'' ≤ ''n''}, then the fit can be assessed using the mean squared error (MSE). The MSE for given estimated parameter values ''a'' and ''β'' on the training set (''x''_''i'', ''y''_''i'') _{1 ≤ ''i'' ≤ ''n''} is defined as:

:$\begin \text &= \frac 1 n \sum_^n (y_i - \hat_i)^2 = \frac 1 n \sum_^n (y_i - a - \boldsymbol\beta^T \mathbf_i)^2\\&= \frac\sum_^n (y_i - a - \beta_1x_ - \dots - \beta_px_)^2 \end$

If the model is correctly specified, it can be shown under mild assumptions that the expected value of the MSE for the training set is (''n'' − ''p'' − 1)/(''n'' + ''p'' + 1) < 1 times the expected value of the MSE for the validation set (the expected value is taken over the distribution of training sets). Thus, a fitted model and computed MSE on the training set will result in an optimistically biased assessment of how well the model will fit an independent data set. This biased estimate is called the ''in-sample'' estimate of the fit, whereas the cross-validation estimate is an ''out-of-sample'' estimate.

Since in linear regression it is possible to directly compute the factor (''n'' − ''p'' − 1)/(''n'' + ''p'' + 1) by which the training MSE underestimates the validation MSE under the assumption that the model specification is valid, cross-validation can be used for checking whether the model has been overfitted, in which case the MSE in the validation set will substantially exceed its anticipated value. (Cross-validation in the context of linear regression is also useful in that it can be used to select an optimally regularized cost function.)
In most other regression procedures (e.g. logistic regression), there is no simple formula to compute the expected out-of-sample fit. Cross-validation is, thus, a generally applicable way to predict the performance of a model on unavailable data using numerical computation in place of theoretical analysis.

Types

Two types of cross-validation can be distinguished: exhaustive and non-exhaustive cross-validation.

Exhaustive cross-validation

Exhaustive cross-validation methods are cross-validation methods which learn and test on all possible ways to divide the original sample into a training and a validation set.

Leave-p-out cross-validation

Leave-''p''-out cross-validation (LpO CV) involves using ''p'' observations as the validation set and the remaining observations as the training set. This is repeated on all ways to cut the original sample on a validation set of ''p'' observations and a training set.

LpO cross-validation require training and validating the model $C^n_p$ times, where ''n'' is the number of observations in the original sample, and where $C^n_p$ is the binomial coefficient. For ''p'' > 1 and for even moderately large ''n'', LpO CV can become computationally infeasible. For example, with ''n'' = 100 and ''p'' = 30, $C^_ \approx 3\times 10^.$

A variant of LpO cross-validation with p=2 known as leave-pair-out cross-validation has been recommended as a nearly unbiased method for estimating the area under ROC curve of binary classifiers.

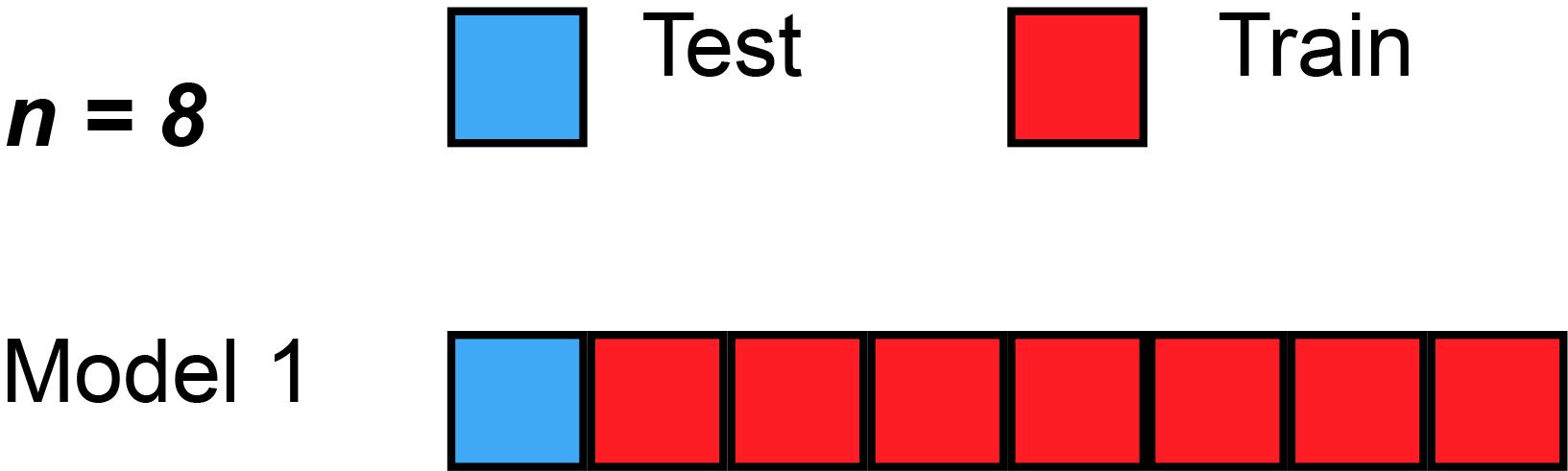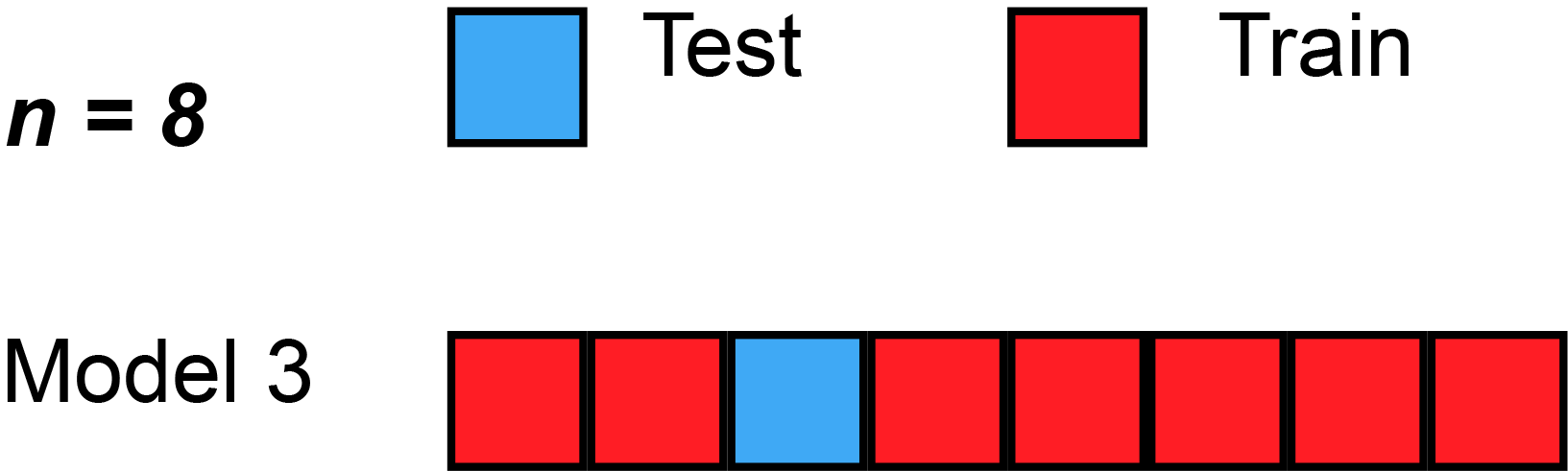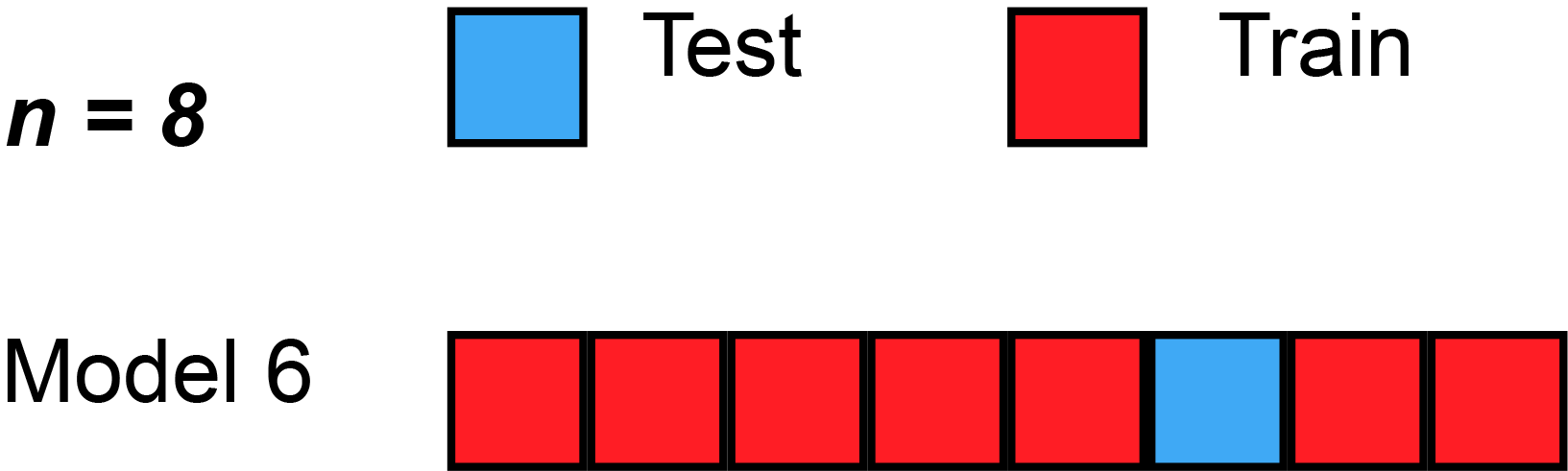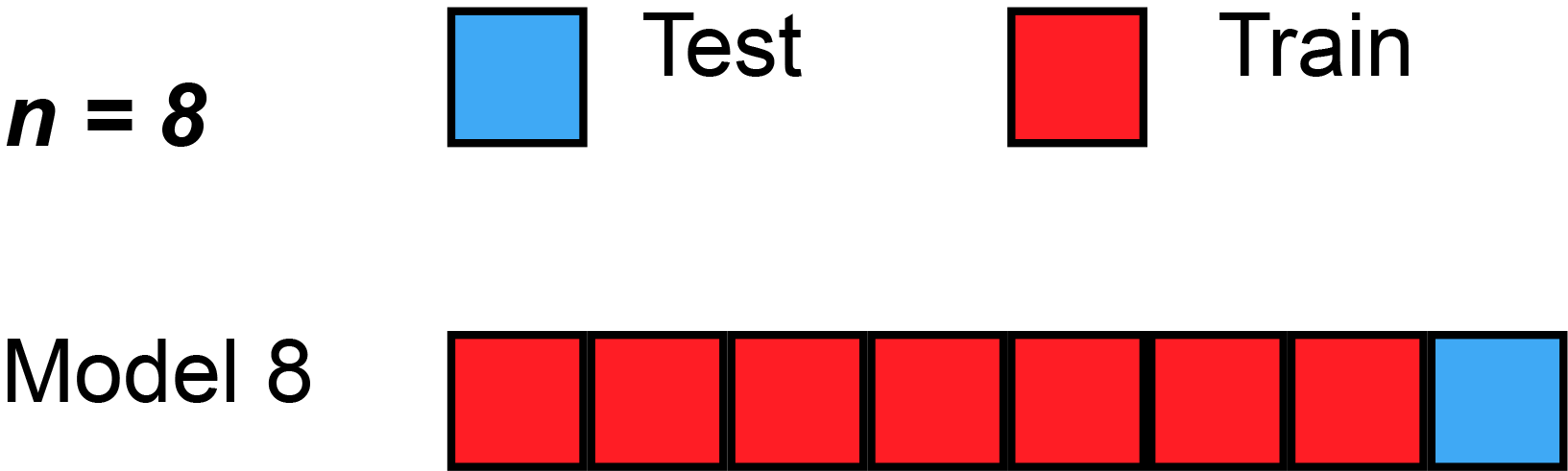
Leave-one-out cross-validation

Leave-''one''-out cross-validation (LOOCV) is a particular case of leave-''p''-out cross-validation with ''p'' = 1.The process looks similar to jackknife; however, with cross-validation one computes a statistic on the left-out sample(s), while with jackknifing one computes a statistic from the kept samples only.

LOO cross-validation requires less computation time than LpO cross-validation because there are only $C^n_1=n$ passes rather than $C^n_p$. However, $n$ passes may still require quite a large computation time, in which case other approaches such as k-fold cross validation may be more appropriate.

Pseudo-code algorithm:

Input:

x,

y,

interpolate( x_in, y_in, x_out ),

Output:

err,

Steps:

err ← 0
for i ← 1, ..., N do
// define the cross-validation subsets
x_in ← (x ..., x − 1 x + 1 ..., x
y_in ← (y ..., y − 1 y + 1 ..., y
x_out ← x y_out ← interpolate(x_in, y_in, x_out)
err ← err + (y − y_out)^2
end for
err ← err/N

Non-exhaustive cross-validation

Non-exhaustive cross validation methods do not compute all ways of splitting the original sample. These methods are approximations of leave-''p''-out cross-validation.

''k''-fold cross-validation

In ''k''-fold cross-validation, the original sample is randomly partitioned into ''k'' equal sized subsamples. Of the ''k'' subsamples, a single subsample is retained as the validation data for testing the model, and the remaining ''k'' − 1 subsamples are used as training data. The cross-validation process is then repeated ''k'' times, with each of the ''k'' subsamples used exactly once as the validation data. The ''k'' results can then be averaged to produce a single estimation. The advantage of this method over repeated random sub-sampling (see below) is that all observations are used for both training and validation, and each observation is used for validation exactly once. 10-fold cross-validation is commonly used, but in general ''k'' remains an unfixed parameter.

For example, setting ''k'' = ''2'' results in 2-fold cross-validation. In 2-fold cross-validation, we randomly shuffle the dataset into two sets ''d''₀ and ''d''₁, so that both sets are equal size (this is usually implemented by shuffling the data array and then splitting it in two). We then train on ''d''₀ and validate on ''d''₁, followed by training on ''d''₁ and validating on ''d''₀.

When ''k'' = ''n'' (the number of observations), ''k''-fold cross-validation is equivalent to leave-one-out cross-validation.

In ''stratified'' ''k''-fold cross-validation, the partitions are selected so that the mean response value is approximately equal in all the partitions. In the case of binary classification, this means that each partition contains roughly the same proportions of the two types of class labels.

In ''repeated'' cross-validation the data is randomly split into ''k'' partitions several times. The performance of the model can thereby be averaged over several runs, but this is rarely desirable in practice.

Holdout method

In the holdout method, we randomly assign data points to two sets ''d''₀ and ''d''₁, usually called the training set and the test set, respectively. The size of each of the sets is arbitrary although typically the test set is smaller than the training set. We then train (build a model) on ''d''₀ and test (evaluate its performance) on ''d''₁.

In typical cross-validation, results of multiple runs of model-testing are averaged together; in contrast, the holdout method, in isolation, involves a single run. It should be used with caution because without such averaging of multiple runs, one may achieve highly misleading results. One's indicator of predictive accuracy ( ''F''^*) will tend to be unstable since it will not be smoothed out by multiple iterations (see below). Similarly, indicators of the specific role played by various predictor variables (e.g., values of regression coefficients) will tend to be unstable.

While the holdout method can be framed as "the simplest kind of cross-validation", many sources instead classify holdout as a type of simple validation, rather than a simple or degenerate form of cross-validation.

Repeated random sub-sampling validation

This method, also known as Monte Carlo cross-validation, creates multiple random splits of the dataset into training and validation data. For each such split, the model is fit to the training data, and predictive accuracy is assessed using the validation data. The results are then averaged over the splits. The advantage of this method (over ''k''-fold cross validation) is that the proportion of the training/validation split is not dependent on the number of iterations (i.e., the number of partitions). The disadvantage of this method is that some observations may never be selected in the validation subsample, whereas others may be selected more than once. In other words, validation subsets may overlap. This method also exhibits Monte Carlo variation, meaning that the results will vary if the analysis is repeated with different random splits.

As the number of random splits approaches infinity, the result of repeated random sub-sampling validation tends towards that of leave-p-out cross-validation.

In a stratified variant of this approach, the random samples are generated in such a way that the mean response value (i.e. the dependent variable in the regression) is equal in the training and testing sets. This is particularly useful if the responses are dichotomous with an unbalanced representation of the two response values in the data.

A method which applies repeated random sub-sampling is RANSAC.

Nested cross-validation

When cross-validation is used simultaneously for selection of the best set of hyperparameters and for error estimation (and assessment of generalization capacity), a nested cross-validation is required. Many variants exist. At least two variants can be distinguished:

k*l-fold cross-validation

This is a truly nested variant which contains an outer loop of ''k'' sets and an inner loop of ''l'' sets. The total data set is split into ''k'' sets. One by one, a set is selected as the (outer) test set and the ''k'' - 1 other sets are combined into the corresponding outer training set. This is repeated for each of the ''k'' sets. Each outer training set is further sub-divided into ''l'' sets. One by one, a set is selected as inner test (validation) set and the ''l'' - 1 other sets are combined into the corresponding inner training set. This is repeated for each of the ''l'' sets. The inner training sets are used to fit model parameters, while the outer test set is used as a validation set to provide an unbiased evaluation of the model fit. Typically, this is repeated for many different hyperparameters (or even different model types) and the validation set is used to determine the best hyperparameter set (and model type) for this inner training set. After this, a new model is fit on the entire outer training set, using the best set of hyperparameters from the inner cross-validation. The performance of this model is then evaluated using the outer test set.

k-fold cross-validation with validation and test set

This is a type of k*l-fold cross-validation when ''l'' = ''k'' - 1. A single k-fold cross-validation is used with both a validation and test set. The total data set is split into ''k'' sets. One by one, a set is selected as test set. Then, one by one, one of the remaining sets is used as a validation set and the other ''k'' - 2 sets are used as training sets until all possible combinations have been evaluated. Similar to the k*l-fold cross validation, the training set is used for model fitting and the validation set is used for model evaluation for each of the hyperparameter sets. Finally, for the selected parameter set, the test set is used to evaluate the model with the best parameter set. Here, two variants are possible: either evaluating the model that was trained on the training set or evaluating a new model that was fit on the combination of the training and the validation set.

Measures of fit

The goal of cross-validation is to estimate the expected level of fit of a model to a data set that is independent of the data that were used to train the model. It can be used to estimate any quantitative measure of fit that is appropriate for the data and model. For example, for binary classification problems, each case in the validation set is either predicted correctly or incorrectly. In this situation the misclassification error rate can be used to summarize the fit, although other measures like positive predictive value could also be used. When the value being predicted is continuously distributed, the mean squared error, root mean squared error or median absolute deviation could be used to summarize the errors.

Using prior information

When users apply cross-validation to select a good configuration $\lambda$, then they might want to balance the cross-validated choice with their own estimate of the configuration. In this way, they can attempt to counter the volatility of cross-validation when the sample size is small and include relevant information from previous research. In a forecasting combination exercise, for instance, cross-validation can be applied to estimate the weights that are assigned to each forecast. Since a simple equal-weighted forecast is difficult to beat, a penalty can be added for deviating from equal weights. Or, if cross-validation is applied to assign individual weights to observations, then one can penalize deviations from equal weights to avoid wasting potentially relevant information. Hoornweg (2018) shows how a tuning parameter $\gamma$ can be defined so that a user can intuitively balance between the accuracy of cross-validation and the simplicity of sticking to a reference parameter $\lambda_R$ that is defined by the user.

If $\lambda_i$ denotes the $i^$ candidate configuration that might be selected, then the loss function that is to be minimized can be defined as
: $L_ = (1-\gamma) \mbox_i + \gamma \mbox_i.$
Relative accuracy can be quantified as $\mbox(\lambda_i)/\mbox(\lambda_R)$, so that the mean squared error of a candidate $\lambda_i$ is made relative to that of a user-specified $\lambda_R$. The relative simplicity term measures the amount that $\lambda_i$ deviates from $\lambda_R$ relative to the maximum amount of deviation from $\lambda_R$. Accordingly, relative simplicity can be specified as $\frac$, where $\lambda_$ corresponds to the $\lambda$ value with the highest permissible deviation from $\lambda_R$. With \gamma\in ,1/math>, the user determines how high the influence of the reference parameter is relative to cross-validation.

One can add relative simplicity terms for multiple configurations $c=1,2,...,C$ by specifying the loss function as
: $L_ = \mbox_i + \sum_^C \frac \mbox_.$
Hoornweg (2018) shows that a loss function with such an accuracy-simplicity tradeoff can also be used to intuitively define shrinkage estimators like the (adaptive) lasso and Bayesian / ridge regression. Click on the lasso for an example.

Statistical properties

Suppose we choose a measure of fit ''F'', and use cross-validation to produce an estimate ''F^*'' of the expected fit ''EF'' of a model to an independent data set drawn from the same population as the training data. If we imagine sampling multiple independent training sets following the same distribution, the resulting values for ''F^*'' will vary. The statistical properties of ''F^*'' result from this variation.

The cross-validation estimator ''F^*'' is very nearly unbiased for ''EF''. The reason that it is slightly biased is that the training set in cross-validation is slightly smaller than the actual data set (e.g. for LOOCV the training set size is ''n'' − 1 when there are ''n'' observed cases). In nearly all situations, the effect of this bias will be conservative in that the estimated fit will be slightly biased in the direction suggesting a poorer fit. In practice, this bias is rarely a concern.

The variance of ''F^*'' can be large. For this reason, if two statistical procedures are compared based on the results of cross-validation, the procedure with the better estimated performance may not actually be the better of the two procedures (i.e. it may not have the better value of ''EF''). Some progress has been made on constructing confidence intervals around cross-validation estimates, but this is considered a difficult problem.

Computational issues

Most forms of cross-validation are straightforward to implement as long as an implementation of the prediction method being studied is available. In particular, the prediction method can be a "black box" – there is no need to have access to the internals of its implementation. If the prediction method is expensive to train, cross-validation can be very slow since the training must be carried out repeatedly. In some cases such as least squares and kernel regression, cross-validation can be sped up significantly by pre-computing certain values that are needed repeatedly in the training, or by using fast "updating rules" such as the Sherman–Morrison formula. However one must be careful to preserve the "total blinding" of the validation set from the training procedure, otherwise bias may result. An extreme example of accelerating cross-validation occurs in linear regression, where the results of cross-validation have a closed-form expression known as the ''prediction residual error sum of squares'' ( PRESS).

Limitations and misuse

Cross-validation only yields meaningful results if the validation set and training set are drawn from the same population and only if human biases are controlled.

In many applications of predictive modeling, the structure of the system being studied evolves over time (i.e. it is "non-stationary"). Both of these can introduce systematic differences between the training and validation sets. For example, if a model for predicting stock values is trained on data for a certain five-year period, it is unrealistic to treat the subsequent five-year period as a draw from the same population. As another example, suppose a model is developed to predict an individual's risk for being diagnosed with a particular disease within the next year. If the model is trained using data from a study involving only a specific population group (e.g. young people or males), but is then applied to the general population, the cross-validation results from the training set could differ greatly from the actual predictive performance.

In many applications, models also may be incorrectly specified and vary as a function of modeler biases and/or arbitrary choices. When this occurs, there may be an illusion that the system changes in external samples, whereas the reason is that the model has missed a critical predictor and/or included a confounded predictor. New evidence is that cross-validation by itself is not very predictive of external validity, whereas a form of experimental validation known as swap sampling that does control for human bias can be much more predictive of external validity. As defined by this large MAQC-II study across 30,000 models, swap sampling incorporates cross-validation in the sense that predictions are tested across independent training and validation samples. Yet, models are also developed across these independent samples and by modelers who are blinded to one another. When there is a mismatch in these models developed across these swapped training and validation samples as happens quite frequently, MAQC-II shows that this will be much more predictive of poor external predictive validity than traditional cross-validation.

The reason for the success of the swapped sampling is a built-in control for human biases in model building. In addition to placing too much faith in predictions that may vary across modelers and lead to poor external validity due to these confounding modeler effects, these are some other ways that cross-validation can be misused:

* By performing an initial analysis to identify the most informative features using the entire data set – if feature selection or model tuning is required by the modeling procedure, this must be repeated on every training set. Otherwise, predictions will certainly be upwardly biased. If cross-validation is used to decide which features to use, an ''inner cross-validation'' to carry out the feature selection on every training set must be performed.
* By allowing some of the training data to also be included in the test set – this can happen due to "twinning" in the data set, whereby some exactly identical or nearly identical samples are present in the data set. To some extent twinning always takes place even in perfectly independent training and validation samples. This is because some of the training sample observations will have nearly identical values of predictors as validation sample observations. And some of these will correlate with a target at better than chance levels in the same direction in both training and validation when they are actually driven by confounded predictors with poor external validity. If such a cross-validated model is selected from a ''k''-fold set, human confirmation bias will be at work and determine that such a model has been validated. This is why traditional cross-validation needs to be supplemented with controls for human bias and confounded model specification like swap sampling and prospective studies.

Cross validation for time-series models

Since the order of the data is important, cross-validation might be problematic for time-series models. A more appropriate approach might be to use rolling cross-validation.

However, if performance is described by a single summary statistic, it is possible that the approach described by Politis and Romano as a stationary bootstrap will work. The statistic of the bootstrap needs to accept an interval of the time series and return the summary statistic on it. The call to the stationary bootstrap needs to specify an appropriate mean interval length.

Applications

Cross-validation can be used to compare the performances of different predictive modeling procedures. For example, suppose we are interested in optical character recognition, and we are considering using either a Support Vector Machine (SVM) or ''k''-nearest neighbors (KNN) to predict the true character from an image of a handwritten character. Using cross-validation, we could objectively compare these two methods in terms of their respective fractions of misclassified characters. If we simply compared the methods based on their in-sample error rates, one method would likely appear to perform better, since it is more flexible and hence more prone to overfitting compared to the other method.

Cross-validation can also be used in ''variable selection''. Suppose we are using the expression levels of 20 proteins to predict whether a cancer patient will respond to a drug. A practical goal would be to determine which subset of the 20 features should be used to produce the best predictive model. For most modeling procedures, if we compare feature subsets using the in-sample error rates, the best performance will occur when all 20 features are used. However under cross-validation, the model with the best fit will generally include only a subset of the features that are deemed truly informative.

A recent development in medical statistics is its use in meta-analysis. It forms the basis of the validation statistic, Vn which is used to test the statistical validity of meta-analysis summary estimates. It has also been used in a more conventional sense in meta-analysis to estimate the likely prediction error of meta-analysis results.

See also

* Boosting (machine learning)
* Bootstrap aggregating (bagging)
** Out-of-bag error
* Bootstrapping (statistics)
* Leakage (machine learning)
* Model selection
* Stability (learning theory)
* Validity (statistics)

Notes and references

{{DEFAULTSORT:Cross-Validation (Statistics)
Model selection
Regression variable selection
Machine learning