Correlation (statistics)

In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related.
Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve.

Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in general, the presence of a correlation is not sufficient to infer the presence of a causal relationship (i.e., correlation does not imply causation).

Formally, random variables are ''dependent'' if they do not satisfy a mathematical property of probabilistic independence. In informal parlance, ''correlation'' is synonymous with ''dependence''. However, when used in a technical sense, correlation refers to any of several specific types of mathematical operations between the tested variables and their respective expected values. Essentially, correlation is the measure of how two or more variables are related to one another. There are several correlation coefficients, often denoted $\rho$ or $r$, measuring the degree of correlation. The most common of these is the ''Pearson correlation coefficient'', which is sensitive only to a linear relationship between two variables (which may be present even when one variable is a nonlinear function of the other). Other correlation coefficients – such as ''Spearman's rank correlation'' – have been developed to be more robust than Pearson's, that is, more sensitive to nonlinear relationships. Mutual information can also be applied to measure dependence between two variables.

Pearson's product-moment coefficient

The most familiar measure of dependence between two quantities is the Pearson product-moment correlation coefficient (PPMCC), or "Pearson's correlation coefficient", commonly called simply "the correlation coefficient". It is obtained by taking the ratio of the covariance of the two variables in question of our numerical dataset, normalized to the square root of their variances. Mathematically, one simply divides the covariance of the two variables by the product of their standard deviations. Karl Pearson developed the coefficient from a similar but slightly different idea by Francis Galton.

A Pearson product-moment correlation coefficient attempts to establish a line of best fit through a dataset of two variables by essentially laying out the expected values and the resulting Pearson's correlation coefficient indicates how far away the actual dataset is from the expected values. Depending on the sign of our Pearson's correlation coefficient, we can end up with either a negative or positive correlation if there is any sort of relationship between the variables of our data set.

The population correlation coefficient $\rho_$ between two random variables $X$ and $Y$ with expected values $\mu_X$ and $\mu_Y$ and standard deviations $\sigma_X$ and $\sigma_Y$ is defined as:

$\rho_ = \operatorname(X,Y) = = , \quad \text\ \sigma_\sigma_>0.$

where $\operatorname$ is the expected value operator, $\operatorname$ means covariance, and $\operatorname$ is a widely used alternative notation for the correlation coefficient. The Pearson correlation is defined only if both standard deviations are finite and positive. An alternative formula purely in terms of moments is:

$\rho_ =$

Correlation and independence

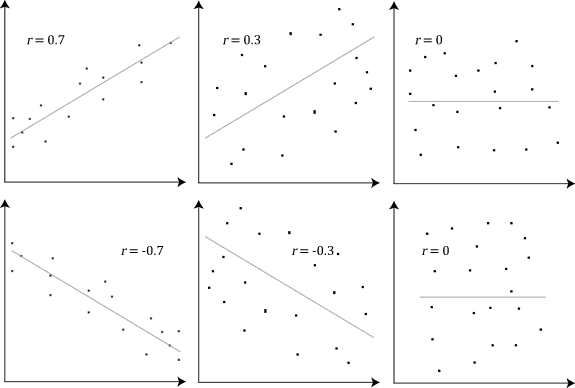
It is a corollary of the Cauchy–Schwarz inequality that the absolute value of the Pearson correlation coefficient is not bigger than 1. Therefore, the value of a correlation coefficient ranges between −1 and +1. The correlation coefficient is +1 in the case of a perfect direct (increasing) linear relationship (correlation), −1 in the case of a perfect inverse (decreasing) linear relationship (anti-correlation), and some value in the open interval $(-1,1)$ in all other cases, indicating the degree of linear dependence between the variables. As it approaches zero there is less of a relationship (closer to uncorrelated). The closer the coefficient is to either −1 or 1, the stronger the correlation between the variables.

If the variables are independent, Pearson's correlation coefficient is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables.

$\begin X,Y \text \quad & \Rightarrow \quad \rho_ = 0 \quad (X,Y \text)\\ \rho_ = 0 \quad (X,Y \text)\quad & \nRightarrow \quad X,Y \text \end$

For example, suppose the random variable $X$ is symmetrically distributed about zero, and $Y=X^2$. Then $Y$ is completely determined by $X$, so that $X$ and $Y$ are perfectly dependent, but their correlation is zero; they are uncorrelated. However, in the special case when $X$ and $Y$ are jointly normal, uncorrelatedness is equivalent to independence.

Even though uncorrelated data does not necessarily imply independence, one can check if random variables are independent if their mutual information is 0.

Sample correlation coefficient

Given a series of $n$ measurements of the pair $(X_i,Y_i)$ indexed by $i=1,\ldots,n$, the ''sample correlation coefficient'' can be used to estimate the population Pearson correlation $\rho_$ between $X$ and $Y$. The sample correlation coefficient is defined as

:$r_ \quad \overset \quad \frac =\frac ,$

where $\overline$ and $\overline$ are the sample means of $X$ and $Y$, and $s_x$ and $s_y$ are the corrected sample standard deviations of $X$ and $Y$.

Equivalent expressions for $r_$ are
:
\begin
r_ &=\frac \\ pt &=\frac.
\end

where $s'_x$ and $s'_y$ are the ''uncorrected'' sample standard deviations of $X$ and $Y$.

If $x$ and $y$ are results of measurements that contain measurement error, the realistic limits on the correlation coefficient are not −1 to +1 but a smaller range. For the case of a linear model with a single independent variable, the coefficient of determination (R squared) is the square of $r_$, Pearson's product-moment coefficient.

Example

Consider the