Conoid Bench George Nakashima 1977

In geometry a conoid () is a ruled surface, whose rulings (lines) fulfill the additional conditions:
:(1) All rulings are parallel to a plane, the '' directrix plane''.
:(2) All rulings intersect a fixed line, the ''axis''.

The conoid is a right conoid if its axis is perpendicular to its directrix plane. Hence all rulings are perpendicular to the axis.

Because of (1) any conoid is a Catalan surface and can be represented parametrically by
:$\mathbf x(u,v)= \mathbf c(u) + v\mathbf r(u)\$
Any curve with fixed parameter is a ruling, describes the ''directrix'' and the vectors are all parallel to the directrix plane. The planarity of the vectors can be represented by
:$\det(\mathbf r,\mathbf \dot r,\mathbf \ddot r)=0$.
If the directrix is a circle, the conoid is called a circular conoid.

The term ''conoid'' was already used by Archimedes in his treatise '' On Conoids and Spheroides''.

Examples

Right circular conoid

The parametric representation
:$\mathbf x(u,v)=(\cos u,\sin u,0) + v (0,-\sin u,z_0) \ ,\ 0\le u <2\pi, v\in \R$
:describes a right circular conoid with the unit circle of the x-y-plane as directrix and a directrix plane, which is parallel to the y--z-plane. Its axis is the line $(x,0,z_0) \ x\in \R \ .$

''Special features'':
# The intersection with a horizontal plane is an ellipse.
# $(1-x^2)(z-z_0)^2-y^2z_0^2=0$ is an implicit representation. Hence the right circular conoid is a surface of degree 4.
# Kepler's rule gives for a right circular conoid with radius $r$ and height $h$ the exact volume: $V=\tfracr^2h$.

The implicit representation is fulfilled by the points of the line $(x,0,z_0)$, too. For these points there exist no tangent planes. Such points are called ''singular''.

Parabolic conoid

The parametric representation
:$\mathbf x(u,v)=\left(1,u,-u^2\right)+ v\left(-1,0,u^2\right)$
:::: $=\left(1-v,u,-(1-v)u^2\right)\ , u,v \in \R \ ,$
describes a ''parabolic conoid'' with the equation $z=-xy^2$. The conoid has a parabola as directrix, the y-axis as axis and a plane parallel to the x-z-plane as directrix plane. It is used by architects as roof surface (s. below).

The parabolic conoid has no singular points.

Further examples

#hyperbolic paraboloid
#Plücker conoid
#Whitney Umbrella
#helicoid

Hyp-paraboloid.svg, hyperbolic paraboloid
Pluecker-conoid.svg, Plücker conoid
Whitney-umbrella.svg, Whitney umbrella

Applications

Mathematics

There are a lot of conoids with singular points, which are investigated in algebraic geometry.

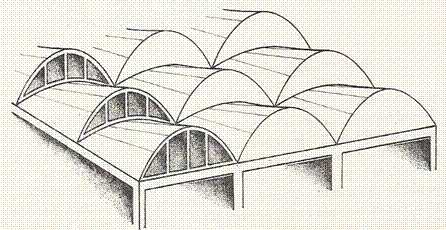
Architecture

Like other ruled surfaces conoids are of high interest with architects, because they can be built using beams or bars. Right conoids can be manufactured easily: one threads bars onto an axis such that they can be rotated around this axis, only. Afterwards one deflects the bars by a directrix and generates a conoid (s. parabolic conoid).

External links

mathworld: Plücker conoid
*

References

* A. Gray, E. Abbena, S. Salamon, ''Modern differential geometry of curves and surfaces with Mathematica'', 3rd ed. Boca Raton, FL:CRC Press, 2006.

()
* Vladimir Y. Rovenskii, ''Geometry of curves and surfaces with MAPLE'

({{ISBN, 978-0-8176-4074-3)

Surfaces
Geometric shapes