Cone And Kimball Building

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex.

A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface.

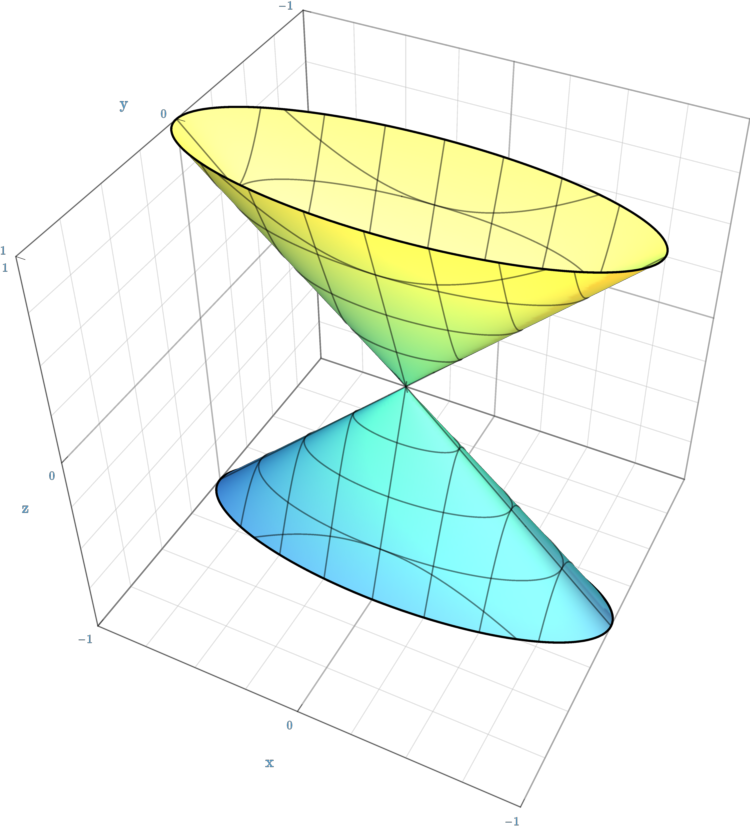
In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a double cone. Either half of a double cone on one side of the apex is called a ''nappe''.

The axis of a cone is the straight line (if any), passing through the apex, about which the base (and the whole cone) has a circular symmetry.

In common usage in elementary geometry, cones are assumed to be right circular, where ''circular'' means that the base is a circle and ''right'' means that the axis passes through the centre of the base at right angles to its plane. If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shapeGrünbaum, ''Convex Polytopes'', second edition, p. 23. and the apex may lie anywhere (though it is usually assumed that the base is bounded and therefore has finite area, and that the apex lies outside the plane of the base). Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly.

A cone with a polygonal base is called a pyramid.

Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.

Cones can also be generalized to higher dimensions.

Further terminology

The perimeter of the base of a cone is called the "directrix", and each of the line segments between the directrix and apex is a "generatrix" or "generating line" of the lateral surface. (For the connection between this sense of the term "directrix" and the directrix of a conic section, see Dandelin spheres.)

The "base radius" of a circular cone is the radius of its base; often this is simply called the radius of the cone. The aperture of a right circular cone is the maximum angle between two generatrix lines; if the generatrix makes an angle ''θ'' to the axis, the aperture is 2''θ''.

A cone with a region including its apex cut off by a plane is called a " truncated cone"; if the truncation plane is parallel to the cone's base, it is called a frustum. An "elliptical cone" is a cone with an elliptical base. A "generalized cone" is the surface created by the set of lines passing through a vertex and every point on a boundary (also see visual hull).

Measurements and equations

Volume

The volume $V$ of any conic solid is one third of the product of the area of the base $A_B$ and the height $h$
:$V = \fracA_B h.$

In modern mathematics, this formula can easily be computed using calculus — it is, up to scaling, the integral $\int x^2 dx = \tfrac x^3$ Without using calculus, the formula can be proven by comparing the cone to a pyramid and applying Cavalieri's principle – specifically, comparing the cone to a (vertically scaled) right square pyramid, which forms one third of a cube. This formula cannot be proven without using such infinitesimal arguments – unlike the 2-dimensional formulae for polyhedral area, though similar to the area of the circle – and hence admitted less rigorous proofs before the advent of calculus, with the ancient Greeks using the method of exhaustion. This is essentially the content of Hilbert's third problem – more precisely, not all polyhedral pyramids are ''scissors congruent'' (can be cut apart into finite pieces and rearranged into the other), and thus volume cannot be computed purely by using a decomposition argument.

Center of mass

The center of mass of a conic solid of uniform density lies one-quarter of the way from the center of the base to the vertex, on the straight line joining the two.

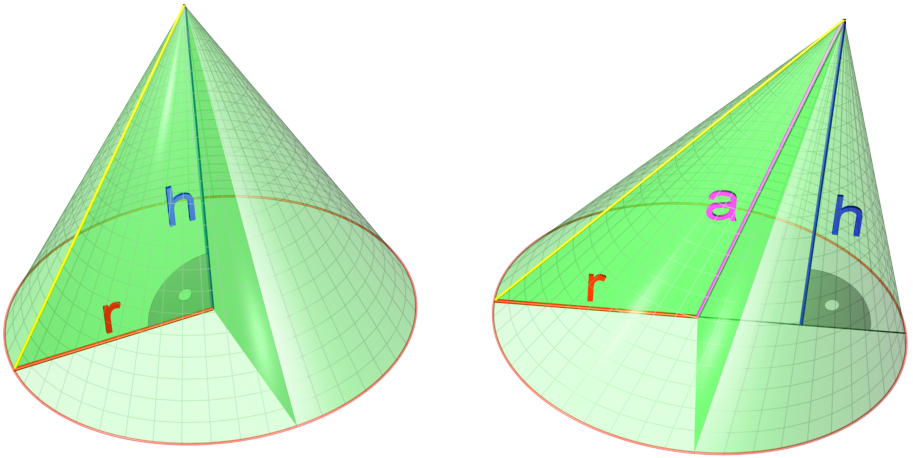
Right circular cone

Volume

For a circular cone with radius ''r'' and height ''h'', the base is a circle of area $\pi r^2$ and so the formula for volume becomes

:$V = \frac \pi r^2 h.$

Slant height

The slant height of a right circular cone is the distance from any point on the circle of its base to the apex via a line segment along the surface of the cone. It is given by $\sqrt$, where $r$ is the radius of the base and $h$ is the height. This can be proved by the Pythagorean theorem.

Surface area

The lateral surface area of a right circular cone is $LSA = \pi r l$ where $r$ is the radius of the circle at the bottom of the cone and $l$ is the slant height of the cone. The surface area of the bottom circle of a cone is the same as for any circle, $\pi r^2$. Thus, the total surface area of a right circular cone can be expressed as each of the following:

*Radius and height
:$\pi r^2+\pi r \sqrt$
:(the area of the base plus the area of the lateral surface; the term $\sqrt$ is the slant height)

:$\pi r \left(r + \sqrt\right)$
:where $r$ is the radius and $h$ is the height.

*Radius and slant height
:$\pi r^2+\pi r l$

:$\pi r(r+l)$
:where $r$ is the radius and $l$ is the slant height.

*Circumference and slant height
:$\frac + \frac 2$

:$\left(\frac c 2\right)\left(\frac c + l\right)$
:where $c$ is the circumference and $l$ is the slant height.

*Apex angle and height
:$\pi h^2 \tan \frac \left(\tan \frac + \sec \frac\right)$
:where $\theta$ is the apex angle and $h$ is the height.

Circular sector

The circular sector obtained by unfolding the surface of one nappe of the cone has:

*radius ''R''
:$R = \sqrt$

*arc length ''L''
:$L = c = 2\pi r$

*central angle ''φ'' in radians
:$\phi = \frac = \frac$

Equation form

The surface of a cone can be parameterized as
:$f(\theta,h) = (h \cos\theta, h \sin\theta, h ),$
where $\theta \in [0,2\pi)$ is the angle "around" the cone, and $h \in \mathbb$ is the "height" along the cone.

A right solid circular cone with height $h$ and aperture $2\theta$, whose axis is the $z$ coordinate axis and whose apex is the origin, is described parametrically as
:$F(s,t,u) = \left(u \tan s \cos t, u \tan s \sin t, u \right)$
where $s,t,u$ range over $[0,\theta)$, $[0,2\pi)$, and $[0,h]$, respectively.

In Implicit function, implicit form, the same solid is defined by the inequalities
:$\,$
where
:$F(x,y,z) = (x^2 + y^2)(\cos\theta)^2 - z^2 (\sin \theta)^2.\,$

More generally, a right circular cone with vertex at the origin, axis parallel to the vector $d$, and aperture $2\theta$, is given by the implicit vector equation $F(u) = 0$ where
:$F(u) = (u \cdot d)^2 - (d \cdot d) (u \cdot u) (\cos \theta)^2$   or   $F(u) = u \cdot d - , d, , u, \cos \theta$
where $u=(x,y,z)$, and $u \cdot d$ denotes the dot product.

Elliptic cone

In the Cartesian coordinate system, an ''elliptic cone'' is the locus of an equation of the form

:$\frac + \frac = z^2 .$

It is an affine image of the right-circular ''unit cone'' with equation $x^2+y^2=z^2\ .$ From the fact, that the affine image of a conic section is a conic section of the same type (ellipse, parabola,...) one gets:
*Any ''plane section'' of an elliptic cone is a conic section.
Obviously, any right circular cone contains circles. This is also true, but less obvious, in the general case (see circular section).

The intersection of an elliptic cone with a concentric sphere is a spherical conic.

Projective geometry

In projective geometry, a cylinder is simply a cone whose apex is at infinity. Intuitively, if one keeps the base fixed and takes the limit as the apex goes to infinity, one obtains a cylinder, the angle of the side increasing as arctan, in the limit forming a right angle. This is useful in the definition of degenerate conics, which require considering the cylindrical conics.

According to G. B. Halsted, a cone is generated similarly to a Steiner conic only with a projectivity and axial pencils (not in perspective) rather than the projective ranges used for the Steiner conic:

"If two copunctual non-costraight axial pencils are projective but not perspective, the meets of correlated planes form a 'conic surface of the second order', or 'cone'."G. B. Halsted (1906) ''Synthetic Projective Geometry'', page 20

Generalizations

The definition of a cone may be extended to higher dimensions; see convex cone. In this case, one says that a convex set ''C'' in the real vector space R^''n'' is a cone (with apex at the origin) if for every vector ''x'' in ''C'' and every nonnegative real number ''a'', the vector ''ax'' is in ''C''. In this context, the analogues of circular cones are not usually special; in fact one is often interested in '' polyhedral cones''.

An even more general concept is the topological cone, which is defined in arbitrary topological spaces.

See also

* Bicone
* Cone (linear algebra)
* Cylinder (geometry)
* Democritus
* Generalized conic
* Hyperboloid
* List of shapes
* Pyrometric cone
* Quadric
* Rotation of axes
* Ruled surface
* Translation of axes

Notes

References

*

External links

*
*
* {{MathWorld , urlname=GeneralizedCone , title=Generalized Cone
* An interactiv
Spinning Cone
from Maths Is Fun

Paper model cone



Cut a Cone
An interactive demonstration of the intersection of a cone with a plane

Elementary shapes
Surfaces