geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...

, two or more objects are said to be ''concentric'' when they share the same center. Any pair of (possibly unalike) objects with well-defined centers can be concentric, including circles,

sphere A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...

regular polygon In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...

s, regular polyhedra, parallelograms, cones, conic sections, and quadrics. Geometric objects are '' coaxial'' if they share the same axis (line of symmetry). Geometric objects with a well-defined axis include circles (any line through the center), spheres, cylinders, conic sections, and surfaces of revolution. Concentric objects are often part of the broad category of '' whorled patterns'', which also includes '' spirals'' (a curve which emanates from a point, moving farther away as it revolves around the point).

Geometric properties

In the

Euclidean plane In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...

, two circles that are concentric necessarily have different radii from each other.. However, circles in three-dimensional space may be concentric, and have the same radius as each other, but nevertheless be different circles. For example, two different meridians of a terrestrial

globe A globe is a spherical Earth, spherical Model#Physical model, model of Earth, of some other astronomical object, celestial body, or of the celestial sphere. Globes serve purposes similar to maps, but, unlike maps, they do not distort the surface ...

are concentric with each other and with the

of the earth (approximated as a sphere). More generally, every two great circles on a sphere are concentric with each other and with the sphere. By Euler's theorem in geometry on the distance between the circumcenter and incenter of a triangle, two concentric circles (with that distance being zero) are the circumcircle and incircle of a triangle

if and only if In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...

the radius of one is twice the radius of the other, in which case the triangle is equilateral. The circumcircle and the incircle of a regular ''n''-gon, and the regular ''n''-gon itself, are concentric. For the circumradius-to-inradius ratio for various ''n'', see Bicentric polygon#Regular polygons. The same can be said of a regular polyhedron's insphere, midsphere and circumsphere. The region of the plane between two concentric circles is an annulus, and analogously the region of space between two concentric spheres is a spherical shell.. For a given point ''c'' in the plane, the set of all circles having ''c'' as their center forms a pencil of circles. Each two circles in the pencil are concentric, and have different radii. Every point in the plane, except for the shared center, belongs to exactly one of the circles in the pencil. Every two disjoint circles, and every hyperbolic pencil of circles, may be transformed into a set of concentric circles by a Möbius transformation.

Applications and examples

The ripples formed by dropping a small object into still water naturally form an expanding system of concentric circles. Evenly spaced circles on the targets used in

target archery Target archery is the most popular form of archery, in which members shoot at stationary circular targets at varying distances. All types of bow – longbow, barebow, Recurve bow, recurve and Compound bow, compound – can be used. In Great Brita ...

or similar sports provide another familiar example of concentric circles.

Coaxial cable Coaxial cable, or coax (pronounced ), is a type of electrical cable consisting of an inner Electrical conductor, conductor surrounded by a concentric conducting Electromagnetic shielding, shield, with the two separated by a dielectric (Insulat ...

is a type of electrical cable in which the combined neutral and earth core completely surrounds the live core(s) in system of concentric cylindrical shells.

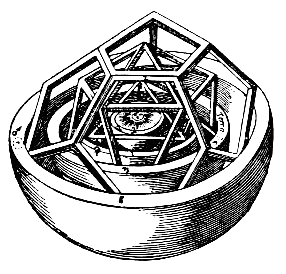
Johannes Kepler Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...

's '' Mysterium Cosmographicum'' envisioned a cosmological system formed by concentric regular polyhedra and spheres. Concentric circles have been used on firearms surfaces as means of holding lubrication or reducing friction on components, similar to jewelling. Concentric circles are also found in diopter sights, a type of mechanic sights commonly found on target rifles. They usually feature a large disk with a small-diameter hole near the shooter's eye, and a front globe sight (a circle contained inside another circle, called ''tunnel''). When these sights are correctly aligned, the point of impact will be in the middle of the front sight circle. File:2006-01-14 Surface waves.jpg, Ripples in water File:Histology of a Pacinian corpuscle.jpg,

Histology Histology, also known as microscopic anatomy or microanatomy, is the branch of biology that studies the microscopic anatomy of biological tissue (biology), tissues. Histology is the microscopic counterpart to gross anatomy, which looks at large ...

of a Pacinian corpuscle, in a typical expanding circular pattern. File:Wooden Piling - dendrochronolgy.jpg, Tree rings, as can be used for tree-ring dating

References

{{reflist

External links

*Geometry
Concentric circles demonstration
With interactive animation Corrosion prevention Geometric centers Visual motifs

Geometric properties

Applications and examples

See also

References

External links