geometry Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...

, two or more objects are said to be concentric, coaxal, or coaxial when they share the same center or axis.

Circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...

s, regular polygons and regular polyhedra, and spheres may be concentric to one another (sharing the same center point), as may

cylinders A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infini ...

(sharing the same central axis).

Geometric properties

In the Euclidean plane, two circles that are concentric necessarily have different radii from each other.. However, circles in three-dimensional space may be concentric, and have the same radius as each other, but nevertheless be different circles. For example, two different meridians of a terrestrial globe are concentric with each other and with the globe of the earth (approximated as a sphere). More generally, every two

great circle In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geomet ...

s on a sphere are concentric with each other and with the sphere. By Euler's theorem in geometry on the distance between the circumcenter and incenter of a triangle, two concentric circles (with that distance being zero) are the

circumcircle In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius. Not every pol ...

and incircle of a triangle if and only if the radius of one is twice the radius of the other, in which case the triangle is equilateral. The circumcircle and the incircle of a regular ''n''-gon, and the regular ''n''-gon itself, are concentric. For the circumradius-to-inradius ratio for various ''n'', see Bicentric polygon#Regular polygons. The same can be said of a regular polyhedron's insphere, midsphere and circumsphere. The region of the plane between two concentric circles is an annulus, and analogously the region of space between two concentric spheres is a spherical shell.. For a given point ''c'' in the plane, the set of all circles having ''c'' as their center forms a pencil of circles. Each two circles in the pencil are concentric, and have different radii. Every point in the plane, except for the shared center, belongs to exactly one of the circles in the pencil. Every two disjoint circles, and every hyperbolic pencil of circles, may be transformed into a set of concentric circles by a

Möbius transformation In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form f(z) = \frac of one complex variable ''z''; here the coefficients ''a'', ''b'', ''c'', ''d'' are complex numbers satisfying ''ad'' ...

Applications and examples

The ripples formed by dropping a small object into still water naturally form an expanding system of concentric circles. Evenly spaced circles on the targets used in target archery or similar sports provide another familiar example of concentric circles.

Coaxial cable Coaxial cable, or coax (pronounced ) is a type of electrical cable consisting of an inner conductor surrounded by a concentric conducting shield, with the two separated by a dielectric ( insulating material); many coaxial cables also have a ...

is a type of electrical cable in which the combined neutral and earth core completely surrounds the live core(s) in system of concentric cylindrical shells.

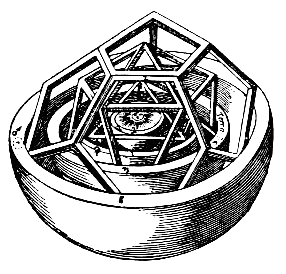
Johannes Kepler Johannes Kepler (; ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his law ...

's '' Mysterium Cosmographicum'' envisioned a cosmological system formed by concentric regular polyhedra and spheres.. Concentric circles are also found in diopter sights, a type of mechanic sights commonly found on target rifles. They usually feature a large disk with a small-diameter hole near the shooter's eye, and a front globe sight (a circle contained inside another circle, called ''tunnel''). When these sights are correctly aligned, the point of impact will be in the middle of the front sight circle.

Geometric properties

Applications and examples

See also