Complementary event

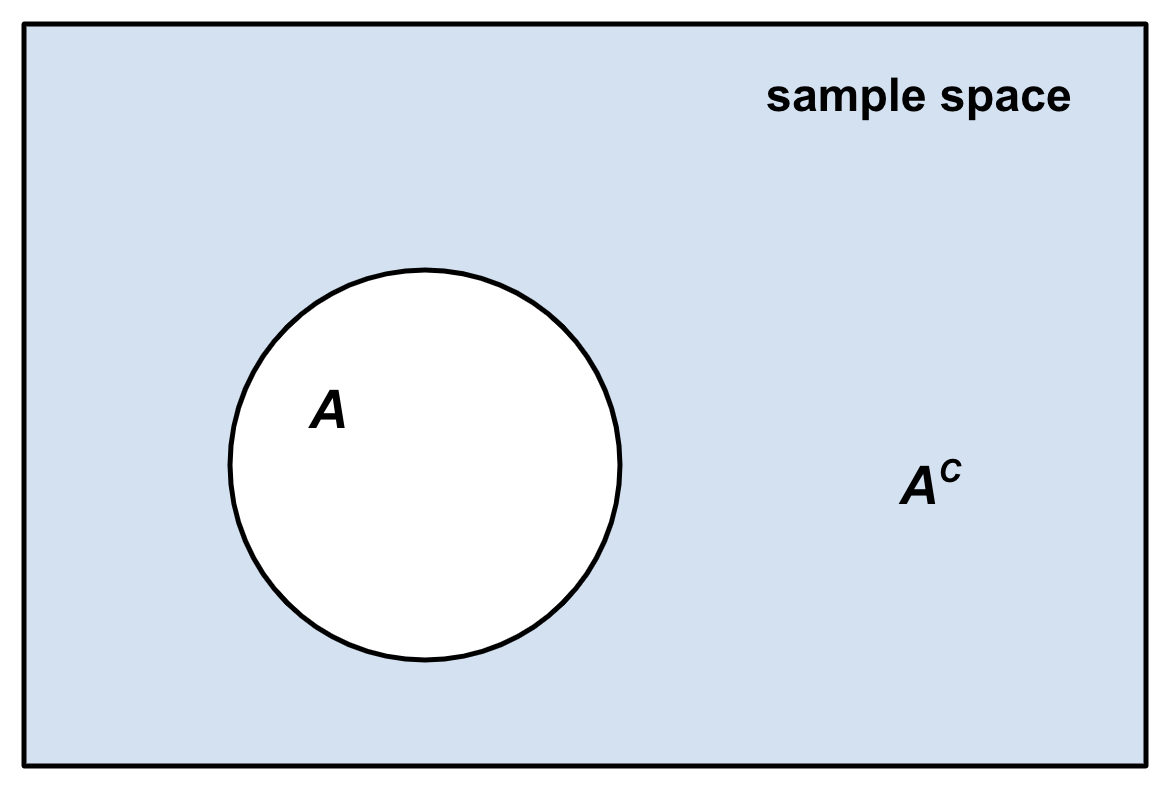
In probability theory, the complement of any event ''A'' is the event ot ''A'' i.e. the event that ''A'' does not occur.Robert R. Johnson, Patricia J. Kuby: ''Elementary Statistics''. Cengage Learning 2007, , p. 229 () The event ''A'' and its complement ot ''A''are mutually exclusive and exhaustive. Generally, there is only one event ''B'' such that ''A'' and ''B'' are both mutually exclusive and exhaustive; that event is the complement of ''A''. The complement of an event ''A'' is usually denoted as ''A′'', ''A^c'', $\neg$''A'' or '. Given an event, the event and its complementary event define a Bernoulli trial: did the event occur or not?

For example, if a typical coin is tossed and one assumes that it cannot land on its edge, then it can either land showing "heads" or "tails." Because these two outcomes are mutually exclusive (i.e. the coin cannot simultaneously show both heads and tails) and collectively exhaustive (i.e. there are no other possible outcomes not represented between these two), they are therefore each other's complements. This means that eadsis logically equivalent to ot tails and ailsis equivalent to ot heads

Complement rule

In a random experiment, the probabilities of all possible events (the sample space) must total to 1— that is, some outcome must occur on every trial. For two events to be complements, they must be collectively exhaustive, together filling the entire sample space. Therefore, the probability of an event's complement must be unity minus the probability of the event. That is, for an event ''A'',
:$P(A^c) = 1 - P(A).$
Equivalently, the probabilities of an event and its complement must always total to 1. This does not, however, mean that ''any'' two events whose probabilities total to 1 are each other's complements; complementary events must also fulfill the condition of mutual exclusivity.

Example of the utility of this concept

Suppose one throws an ordinary six-sided die eight times. What is the probability that one sees a "1" at least once?

It may be tempting to say that

: Pr( 1" on 1st trialor 1" on second trialor ... or 1" on 8th trial

:= Pr("1" on 1st trial) + Pr("1" on second trial) + ... + P("1" on 8th trial)

:= 1/6 + 1/6 + ... + 1/6

:= 8/6

:= 1.3333...

This result cannot be right because a probability cannot be more than 1. The technique is wrong because the eight events whose probabilities got added are not mutually exclusive.

One may resolve this overlap by the principle of inclusion-exclusion, or, in this case, by simply finding the probability of the complementary event and subtracting it from 1, thus:

: Pr(at least one "1") = 1 − Pr(no "1"s)

:= 1 − Pr( o "1" on 1st trialand o "1" on 2nd trialand ... and o "1" on 8th trial

:= 1 − Pr(no "1" on 1st trial) × Pr(no "1" on 2nd trial) × ... × Pr(no "1" on 8th trial)

:= 1 −(5/6) × (5/6) × ... × (5/6)

:= 1 − (5/6)⁸

:= 0.7674...

See also

*Logical complement
* Exclusive disjunction
* Binomial probability

References

External links

''Complementary events''
- (free) page from probability book of McGraw-Hill

{{DEFAULTSORT:Complementary Event
Experiment (probability theory)