Communication-avoiding algorithm

Communication-avoiding algorithms minimize movement of data within a memory hierarchy for improving its running-time and energy consumption. These minimize the total of two costs (in terms of time and energy): arithmetic and communication. Communication, in this context refers to moving data, either between levels of memory or between multiple processors over a network. It is much more expensive than arithmetic.

Formal theory

Two-level memory model

A common computational model in analyzing communication-avoiding algorithms is the two-level memory model:

* There is one processor and two levels of memory.
* Level 1 memory is infinitely large. Level 0 memory ("cache") has size $M$.
* In the beginning, input resides in level 1. In the end, the output resides in level 1.
* Processor can only operate on data in cache.
* The goal is to minimize data transfers between the two levels of memory.

Matrix multiplication

Corollary 6.2:

More general results for other numerical linear algebra operations can be found in. The following proof is from.

Motivation

Consider the following running-time model:

* Measure of computation = Time per FLOP = γ
* Measure of communication = No. of words of data moved = β
⇒ Total running time = γ·(no. of FLOPs) + β·(no. of words)

From the fact that ''β'' >> ''γ'' as measured in time and energy, communication cost dominates computation cost. Technological trends indicate that the relative cost of communication is increasing on a variety of platforms, from cloud computing to supercomputers to mobile devices. The report also predicts that gap between DRAM access time and FLOPs will increase 100× over coming decade to balance power usage between processors and DRAM.

Energy consumption increases by orders of magnitude as we go higher in the memory hierarchy.

United States president Barack Obama cited communication-avoiding algorithms in the FY 2012 Department of Energy budget request to Congress:

Objectives

Communication-avoiding algorithms are designed with the following objectives:

* Reorganize algorithms to reduce communication across all memory hierarchies.
* Attain the lower-bound on communication when possible.

The following simple example demonstrates how these are achieved.

Matrix multiplication example

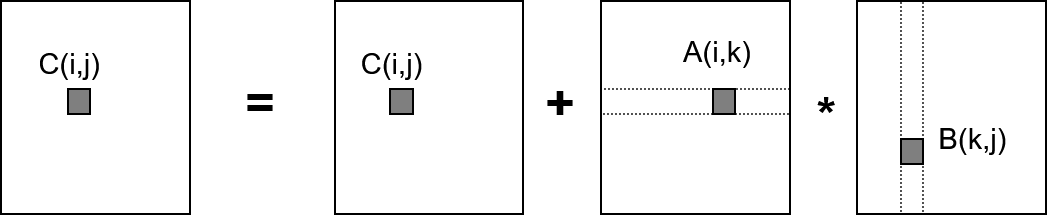
Let A, B and C be square matrices of order ''n'' × ''n''. The following naive algorithm implements C = C + A * B:

for i = 1 to n
for j = 1 to n
for k = 1 to n
C(i,j) = C(i,j) + A(i,k) * B(k,j)

Arithmetic cost (time-complexity): ''n''²(2''n'' − 1) for sufficiently large ''n'' or O(''n''³).

Rewriting this algorithm with communication cost labelled at each step

for i = 1 to n
- n² reads
for j = 1 to n
- n² reads
- n³ reads
for k = 1 to n
C(i,j) = C(i,j) + A(i,k) * B(k,j)
- n² writes

Fast memory may be defined as the local processor memory (CPU cache) of size M and slow memory may be defined as the DRAM.

Communication cost (reads/writes): ''n''³ + 3''n''² or O(''n''³)

Since total running time = ''γ''·O(''n''³) + ''β''·O(''n''³) and ''β'' >> ''γ'' the communication cost is dominant. The blocked (tiled) matrix multiplication algorithm reduces this dominant term:

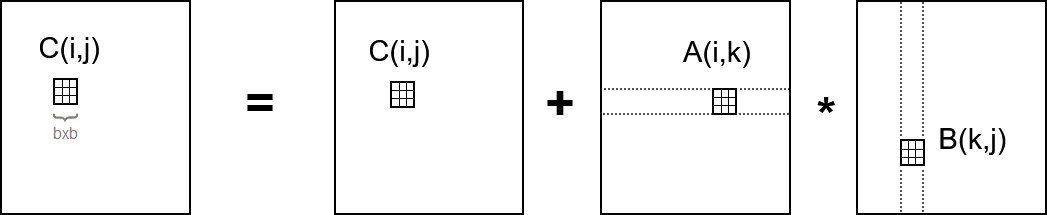
Blocked (tiled) matrix multiplication

Consider A, B and C to be ''n''/''b''-by-''n''/''b'' matrices of ''b''-by-''b'' sub-blocks where b is called the block size; assume three ''b''-by-''b'' blocks fit in fast memory.

for i = 1 to n/b
for j = 1 to n/b
- b² × (n/b)² = n² reads
for k = 1 to n/b
- b² × (n/b)³ = n³/b reads
- b² × (n/b)³ = n³/b reads
C(i,j) = C(i,j) + A(i,k) * B(k,j) -
- b² × (n/b)² = n² writes

Communication cost: 2''n''³/''b'' + 2''n''² reads/writes << 2''n''³ arithmetic cost

Making ''b'' as large possible:
: 3''b''² ≤ ''M''
we achieve the following communication lower bound:
: 3^1/2''n''³/''M''^1/2 + 2''n''² or Ω (no. of FLOPs / ''M''^1/2)

Previous approaches for reducing communication

Most of the approaches investigated in the past to address this problem rely on scheduling or tuning techniques that aim at overlapping communication with computation. However, this approach can lead to an improvement of at most a factor of two. Ghosting is a different technique for reducing communication, in which a processor stores and computes redundantly data from neighboring processors for future computations. Cache-oblivious algorithms represent a different approach introduced in 1999 for fast Fourier transforms, and then extended to graph algorithms, dynamic programming, etc. They were also applied to several operations in linear algebra as dense LU and QR factorizations. The design of architecture specific algorithms is another approach that can be used for reducing the communication in parallel algorithms, and there are many examples in the literature of algorithms that are adapted to a given communication topology.

See also

* Data locality

References

{{reflist, refs=
Demmel, Jim. "Communication avoiding algorithms". 2012 SC Companion: High Performance Computing, Networking Storage and Analysis. IEEE, 2012.
Demmel, James, and Kathy Yelick. "Communication Avoiding (CA) and Other Innovative Algorithms". The Berkeley Par Lab: Progress in the Parallel Computing Landscape: 243–250.
Bergman, Keren, et al.
Exascale computing study: Technology challenges in exascale computing systems
" Defense Advanced Research Projects Agency Information Processing Techniques Office (DARPA IPTO), Tech. Rep 15 (2008).
Shalf, John, Sudip Dosanjh, and John Morrison. "Exascale computing technology challenges". High Performance Computing for Computational Science–VECPAR 2010. Springer Berlin Heidelberg, 2011. 1–25.
M. Frigo, C. E. Leiserson, H. Prokop, and S. Ramachandran, "Cacheoblivious algorithms", In FOCS '99: Proceedings of the 40th Annual Symposium on Foundations of Computer Science, 1999. IEEE Computer Society.
S. Toledo,
Locality of reference in LU Decomposition with partial pivoting
" SIAM J. Matrix Anal. Appl., vol. 18, no. 4, 1997.
F. Gustavson, "Recursion Leads to Automatic Variable Blocking for Dense Linear-Algebra Algorithms," IBM Journal of Research and Development, vol. 41, no. 6, pp. 737–755, 1997.
E. Elmroth, F. Gustavson, I. Jonsson, and B. Kagstrom,
Recursive blocked algorithms and hybrid data structures for dense matrix library software
" SIAM Review, vol. 46, no. 1, pp. 3–45, 2004.
Grigori, Laura.
Introduction to communication avoiding linear algebra algorithms in high performance computing

Parallel computing
Algorithms
Optimization algorithms and methods