Classical Heisenberg Ferromagnet Model (spin Chain)

A spin wave is a propagating disturbance in the ordering of a magnetic material. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are bosonic modes of the spin lattice that correspond roughly to the phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a ferromagnet's spontaneous magnetization. The energies of spin waves are typically only in keeping with typical Curie points at room temperature and below.

Theory

The simplest way of understanding spin waves is to consider the Hamiltonian $\mathcal$ for the Heisenberg ferromagnet:

:$\mathcal = -\frac J \sum_ \mathbf_i \cdot \mathbf_j - g \mu_ \sum_i \mathbf \cdot \mathbf_i$

where is the exchange energy, the operators represent the spins at Bravais lattice points, is the Landé -factor, is the Bohr magneton and is the internal field which includes the external field plus any "molecular" field. Note that in the classical continuum case and in dimensions Heisenberg ferromagnet equation has the form

:$\mathbf_t=\mathbf \times \mathbf_.$

In and dimensions this equation admits several integrable and non-integrable extensions like the Landau-Lifshitz equation, the Ishimori equation and so on. For a ferromagnet and the ground state of the Hamiltonian $, 0\rangle$ is that in which all spins are aligned parallel with the field . That $, 0\rangle$ is an eigenstate of $\mathcal$ can be verified by rewriting it in terms of the spin-raising and spin-lowering operators given by:

:$S^\pm = S^x \pm i S^y$

resulting in

:$\mathcal = -\frac J \sum_ S^z_i S^z_j - g \mu_ H \sum_i S^z_i - \frac J \sum_ (S^+_i S^-_j + S^-_i S^+_j)$

where has been taken as the direction of the magnetic field. The spin-lowering operator annihilates the state with minimum projection of spin along the -axis, while the spin-raising operator annihilates the ground state with maximum spin projection along the -axis. Since

:$S^z_i, 0\rangle = s, 0\rangle$

for the maximally aligned state, we find

:$\mathcal , 0\rangle = \left (-Js^2 -g \mu_ H s \right )N, 0\rangle$

where N is the total number of Bravais lattice sites. The proposition that the ground state is an eigenstate of the Hamiltonian is confirmed.

One might guess that the first excited state of the Hamiltonian has one randomly selected spin at position rotated so that

:$S^z_i , 1\rangle = (s-1), 1\rangle,$

but in fact this arrangement of spins is not an eigenstate. The reason is that such a state is transformed by the spin raising and lowering operators. The operator $S^+_i$ will increase the -projection of the spin at position back to its low-energy orientation, but the operator $S^_j$ will lower the -projection of the spin at position . The combined effect of the two operators is therefore to propagate the rotated spin to a new position, which is a hint that the correct eigenstate is a spin wave, namely a superposition of states with one reduced spin. The exchange energy penalty associated with changing the orientation of one spin is reduced by spreading the disturbance over a long wavelength. The degree of misorientation of any two near-neighbor spins is thereby minimized. From this explanation one can see why the Ising model magnet with discrete symmetry has no spin waves: the notion of spreading a disturbance in the spin lattice over a long wavelength makes no sense when spins have only two possible orientations. The existence of low-energy excitations is related to the fact that in the absence of an external field, the spin system has an infinite number of degenerate ground states with infinitesimally different spin orientations. The existence of these ground states can be seen from the fact that the state $, 0\rangle$ does not have the full rotational symmetry of the Hamiltonian $\mathcal$, a phenomenon which is called spontaneous symmetry breaking.

Magnetization

In this model the magnetization

:$M = \frac$

where is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:

:$\frac = -\gamma\mathbf M \times\mathbf H - \frac$

where is the gyromagnetic ratio and is the damping constant. The cross-products in this forbidding-looking equation show that the propagation of spin waves is governed by the torques generated by internal and external fields. (An equivalent form is the Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simply looking" equivalent one.)

The first term on the right hand side of the equation describes the precession of the magnetization under the influence of the applied field, while the above-mentioned final term describes how the magnetization vector "spirals in" towards the field direction as time progresses. In metals the damping forces described by the constant are in many cases dominated by the eddy currents.

One important difference between phonons and magnons lies in their dispersion relations. The dispersion relation for phonons is to first order linear in wavevector , namely , where is frequency, and is the velocity of sound. Magnons have a parabolic dispersion relation: where the parameter represents a " spin stiffness." The form is the third term of a Taylor expansion of a cosine term in the energy expression originating from the dot-product. 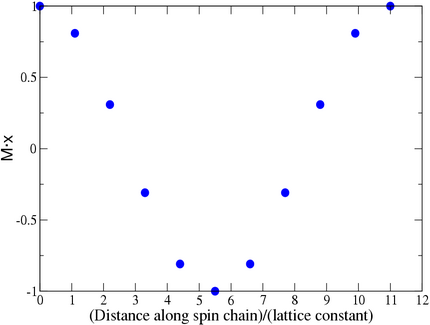The underlying reason for the difference in dispersion relation is that the order parameter (magnetization) for the ground-state in ferromagnets violates time-reversal symmetry. Two adjacent spins in a solid with lattice constant that participate in a mode with wavevector have an angle between them equal to .

Experimental observation

Spin waves are observed through four experimental methods: inelastic neutron scattering, inelastic light scattering (Brillouin scattering, Raman scattering and inelastic X-ray scattering), inelastic electron scattering (spin-resolved electron energy loss spectroscopy), and spin-wave resonance ( ferromagnetic resonance). In the first method the energy loss of a beam of neutrons that excite a magnon is measured, typically as a function of scattering vector (or equivalently momentum transfer), temperature and external magnetic field. Inelastic neutron scattering measurements can determine the dispersion curve for magnons just as they can for phonons. Important inelastic neutron scattering facilities are present at the ISIS neutron source in Oxfordshire, UK, the Institut Laue-Langevin in Grenoble, France, the High Flux Isotope Reactor at Oak Ridge National Laboratory in Tennessee, USA, and at the National Institute of Standards and Technology in Maryland, USA. Brillouin scattering similarly measures the energy loss of photons (usually at a convenient visible wavelength) reflected from or transmitted through a magnetic material. Brillouin spectroscopy is similar to the more widely known Raman scattering, but probes a lower energy and has a superior energy resolution in order to be able to detect the meV energy of magnons. Ferromagnetic (or antiferromagnetic) resonance instead measures the absorption of microwaves, incident on a magnetic material, by spin waves, typically as a function of angle, temperature and applied field. Ferromagnetic resonance is a convenient laboratory method for determining the effect of magnetocrystalline anisotropy on the dispersion of spin waves. One group at the Max Planck Institute of Microstructure Physics in Halle, Germany proved that by using spin polarized electron energy loss spectroscopy (SPEELS), very high energy surface magnons can be excited. This technique allows one to probe the dispersion of magnons in the ultrathin ferromagnetic films. The first experiment was performed for a 5 ML Fe film. With momentum resolution, the magnon dispersion was explored for an 8 ML fcc Co film on Cu(001) and an 8 ML hcp Co on W(110), respectively. The maximum magnon energy at the border of the surface Brillouin zone was 240 meV.

Practical significance

When magnetoelectronic devices are operated at high frequencies, the generation of spin waves can be an important energy loss mechanism. Spin wave generation limits the linewidths and therefore the quality factors ''Q'' of ferrite components used in microwave devices. The reciprocal of the lowest frequency of the characteristic spin waves of a magnetic material gives a time scale for the switching of a device based on that material.

See also

* Magnonics
* Holstein–Primakoff transformation
* Spin engineering

References

*
*
*
*
{{Refend

External links

Spin Waves
Biennial International Symposium for discussion of the latest advances in fundamental studies of dynamic properties of various magnetically ordered materials.


performing Brillouin scattering measurements.

Magnetic ordering
Waves

de:Spinwelle
pl:Fale spinowe