Center Of Mass on:
[Wikipedia]
[Google]
[Amazon]
 In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative
 A body's center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform, the mass-center and the center-of-gravity will be the same. However, for satellites in orbit around a planet, in the absence of other torques being applied to a satellite, the slight variation (gradient) in gravitational field between closer-to (stronger) and further-from (weaker) the planet can lead to a torque that will tend to align the satellite such that its long axis is vertical. In such a case, it is important to make the distinction between the center-of-gravity and the mass-center. Any horizontal offset between the two will result in an applied torque.
It is useful to note that the mass-center is a fixed property for a given rigid body (e.g. with no slosh or articulation), whereas the center-of-gravity may, in addition, depend upon its orientation in a non-uniform gravitational field. In the latter case, the center-of-gravity will always be located somewhat closer to the main attractive body as compared to the mass-center, and thus will change its position in the body of interest as its orientation is changed.
In the study of the dynamics of aircraft, vehicles and vessels, forces and moments need to be resolved relative to the mass center. That is true independent of whether gravity itself is a consideration. Referring to the mass-center as the center-of-gravity is something of a colloquialism, but it is in common usage and when gravity gradient effects are negligible, center-of-gravity and mass-center are the same and are used interchangeably.
In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body. Consider a body Q of volume V with density ρ(r) at each point r in the volume. In a parallel gravity field the force f at each point r is given by,
where dm is the mass at the point r, g is the acceleration of gravity, and is a unit vector defining the vertical direction.
Choose a reference point R in the volume and compute the resultant force and torque at this point,
and
If the reference point R is chosen so that it is the center of mass, then
which means the resultant torque T = 0. Because the resultant torque is zero the body will move as though it is a particle with its mass concentrated at the center of mass.
By selecting the center of gravity as the reference point for a rigid body, the gravity forces will not cause the body to rotate, which means the weight of the body can be considered to be concentrated at the center of mass.
A body's center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform, the mass-center and the center-of-gravity will be the same. However, for satellites in orbit around a planet, in the absence of other torques being applied to a satellite, the slight variation (gradient) in gravitational field between closer-to (stronger) and further-from (weaker) the planet can lead to a torque that will tend to align the satellite such that its long axis is vertical. In such a case, it is important to make the distinction between the center-of-gravity and the mass-center. Any horizontal offset between the two will result in an applied torque.
It is useful to note that the mass-center is a fixed property for a given rigid body (e.g. with no slosh or articulation), whereas the center-of-gravity may, in addition, depend upon its orientation in a non-uniform gravitational field. In the latter case, the center-of-gravity will always be located somewhat closer to the main attractive body as compared to the mass-center, and thus will change its position in the body of interest as its orientation is changed.
In the study of the dynamics of aircraft, vehicles and vessels, forces and moments need to be resolved relative to the mass center. That is true independent of whether gravity itself is a consideration. Referring to the mass-center as the center-of-gravity is something of a colloquialism, but it is in common usage and when gravity gradient effects are negligible, center-of-gravity and mass-center are the same and are used interchangeably.
In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body. Consider a body Q of volume V with density ρ(r) at each point r in the volume. In a parallel gravity field the force f at each point r is given by,
where dm is the mass at the point r, g is the acceleration of gravity, and is a unit vector defining the vertical direction.
Choose a reference point R in the volume and compute the resultant force and torque at this point,
and
If the reference point R is chosen so that it is the center of mass, then
which means the resultant torque T = 0. Because the resultant torque is zero the body will move as though it is a particle with its mass concentrated at the center of mass.
By selecting the center of gravity as the reference point for a rigid body, the gravity forces will not cause the body to rotate, which means the weight of the body can be considered to be concentrated at the center of mass.
 The experimental determination of a body's centre of mass makes use of gravity forces on the body and is based on the fact that the centre of mass is the same as the centre of gravity in the parallel gravity field near the earth's surface.
The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.
The experimental determination of a body's centre of mass makes use of gravity forces on the body and is based on the fact that the centre of mass is the same as the centre of gravity in the parallel gravity field near the earth's surface.
The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.
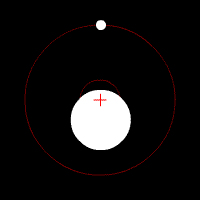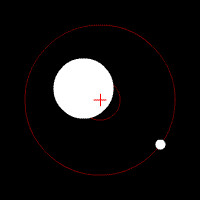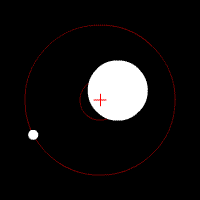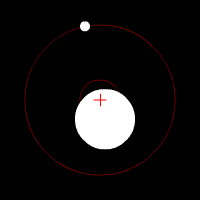 The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the ''barycenter''. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a
The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the ''barycenter''. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a
Motion of the Center of Mass
shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
simulations showing the effect each planet contributes to the Solar System's barycenter. {{DEFAULTSORT:Center Of Mass Classical mechanics Mass Mass Moment (physics)
 In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position
Position often refers to:
* Position (geometry), the spatial location (rather than orientation) of an entity
* Position, a job or occupation
Position may also refer to:
Games and recreation
* Position (poker), location relative to the dealer
* ...
of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration
In physics, angular acceleration refers to the time rate of change of angular velocity. As there are two types of angular velocity, namely spin angular velocity and orbital angular velocity, there are naturally also two types of angular acceler ...
. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.
In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe
A horseshoe is a fabricated product designed to protect a horse hoof from wear. Shoes are attached on the palmar surface (ground side) of the hooves, usually nailed through the insensitive hoof wall that is anatomically akin to the human toen ...
. In the case of a distribution of separate bodies, such as the planets
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a young ...
of the Solar System, the center of mass may not correspond to the position of any individual member of the system.
The center of mass is a useful reference point for calculations in mechanics that involve masses distributed in space, such as the linear and angular momentum of planetary bodies and rigid body dynamics. In orbital mechanics, the equations of motion of planets are formulated as point masses located at the centers of mass. The center of mass frame
In physics, the center-of-momentum frame (also zero-momentum frame or COM frame) of a system is the unique (up to velocity but not origin) inertial frame in which the total momentum of the system vanishes. The ''center of momentum'' of a system is ...
is an inertial frame
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
in which the center of mass of a system is at rest with respect to the origin of the coordinate system.
History
The concept of center of gravity or weight was studied extensively by the ancient Greek mathematician, physicist, and engineer Archimedes of Syracuse. He worked with simplified assumptions about gravity that amount to a uniform field, thus arriving at the mathematical properties of what we now call the center of mass. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point—their center of mass. In his work '' On Floating Bodies'', Archimedes demonstrated that the orientation of a floating object is the one that makes its center of mass as low as possible. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes. Other ancient mathematicians who contributed to the theory of the center of mass include Hero of Alexandria and Pappus of Alexandria. In the Renaissance and Early Modern periods, work by Guido Ubaldi,Francesco Maurolico
Francesco Maurolico (Latin: ''Franciscus Maurolycus''; Italian: ''Francesco Maurolico''; gr, Φραγκίσκος Μαυρόλυκος, 16 September 1494 - 21/22 July 1575) was a mathematician and astronomer from Sicily. He made contributions t ...
, Federico Commandino, Evangelista Torricelli, Simon Stevin
Simon Stevin (; 1548–1620), sometimes called Stevinus, was a Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated vario ...
, Luca Valerio
Luca Valerio (1553–1618) was an Italian mathematician. He developed ways to find volumes and centers of gravity of solid bodies using the methods of Archimedes. He corresponded with Galileo Galilei and was a member of the Accademia dei Lince ...
, Jean-Charles de la Faille, Paul Guldin, John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal ...
, Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of ...
, Louis Carré, Pierre Varignon
Pierre Varignon (1654 – 23 December 1722) was a French mathematician. He was educated at the Jesuit College and the University of Caen, where he received his M.A. in 1682. He took Holy Orders the following year.
Varignon gained his first ex ...
, and Alexis Clairaut expanded the concept further.
Newton's second law is reformulated with respect to the center of mass in Euler's first law.
Definition
The center of mass is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero. In analogy to statistics, the center of mass is the mean location of a distribution of mass in space.A system of particles
In the case of a system of particles , each with mass that are located in space with coordinates , the coordinates R of the center of mass satisfy the condition Solving this equation for R yields the formula where is the total mass of all of the particles.A continuous volume
If the mass distribution is continuous with the density ρ(r) within a solid ''Q'', then the integral of the weighted position coordinates of the points in this volume relative to the center of mass R over the volume V is zero, that is Solve this equation for the coordinates R to obtain where M is the total mass in the volume. If a continuous mass distribution has uniform density, which means ρ is constant, then the center of mass is the same as the centroid of the volume.Barycentric coordinates
The coordinates R of the center of mass of a two-particle system, ''P''1 and ''P''2, with masses ''m''1 and ''m''2 is given by Let the percentage of the total mass divided between these two particles vary from 100% ''P''1 and 0% ''P''2 through 50% ''P''1 and 50% ''P''2 to 0% ''P''1 and 100% ''P''2, then the center of mass R moves along the line from ''P''1 to ''P''2. The percentages of mass at each point can be viewed as projective coordinates of the point R on this line, and are termed barycentric coordinates. Another way of interpreting the process here is the mechanical balancing of moments about an arbitrary point. The numerator gives the total moment that is then balanced by an equivalent total force at the center of mass. This can be generalized to three points and four points to define projective coordinates in the plane, and in space, respectively.Systems with periodic boundary conditions
For particles in a system withperiodic boundary conditions
Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a ''unit cell''. PBCs are often used in computer simulations and mathematical mode ...
two particles can be neighbours even though they are on opposite sides of the system. This occurs often in molecular dynamics simulations, for example, in which clusters form at random locations and sometimes neighbouring atoms cross the periodic boundary. When a cluster straddles the periodic boundary, a naive calculation of the center of mass will be incorrect. A generalized method for calculating the center of mass for periodic systems is to treat each coordinate, ''x'' and ''y'' and/or ''z'', as if it were on a circle instead of a line. The calculation takes every particle's ''x'' coordinate and maps it to an angle,
where ''x''max is the system size in the ''x'' direction and . From this angle, two new points can be generated, which can be weighted by the mass of the particle for the center of mass or given a value of 1 for the geometric center:
In the plane, these coordinates lie on a circle of radius 1. From the collection of and values from all the particles, the averages and are calculated.
where is the sum of the masses of all of the particles.
These values are mapped back into a new angle, , from which the ''x'' coordinate of the center of mass can be obtained:
The process can be repeated for all dimensions of the system to determine the complete center of mass. The utility of the algorithm is that it allows the mathematics to determine where the "best" center of mass is, instead of guessing or using cluster analysis to "unfold" a cluster straddling the periodic boundaries. If both average values are zero, , then is undefined. This is a correct result, because it only occurs when all particles are exactly evenly spaced. In that condition, their ''x'' coordinates are mathematically identical in a periodic system.
Center of gravity
Linear and angular momentum
The linear and angular momentum of a collection of particles can be simplified by measuring the position and velocity of the particles relative to the center of mass. Let the system of particles ''Pi'', ''i'' = 1, ..., ''n'' of masses ''mi'' be located at the coordinates r''i'' with velocities v''i''. Select a reference point R and compute the relative position and velocity vectors, The total linear momentum and angular momentum of the system are and If R is chosen as the center of mass these equations simplify to where ''m'' is the total mass of all the particles, p is the linear momentum, and L is the angular momentum. The law of conservation of momentum predicts that for any system not subjected to external forces the momentum of the system will remain constant, which means the center of mass will move with constant velocity. This applies for all systems with classical internal forces, including magnetic fields, electric fields, chemical reactions, and so on. More formally, this is true for any internal forces that cancel in accordance with Newton's Third Law.Locating the center of mass
In two dimensions
An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass. The shape of an object might already be mathematically determined, but it may be too complex to use a known formula. In this case, one can subdivide the complex shape into simpler, more elementary shapes, whose centers of mass are easy to find. If the total mass and center of mass can be determined for each area, then the center of mass of the whole is the weighted average of the centers. This method can even work for objects with holes, which can be accounted for as negative masses. A direct development of the planimeter known as an integraph, or integerometer, can be used to establish the position of the centroid or center of mass of an irregular two-dimensional shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to compare with the required displacement andcenter of buoyancy
Buoyancy (), or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pr ...
of a ship, and ensure it would not capsize.
In three dimensions
An experimental method to locate the three-dimensional coordinates of the center of mass begins by supporting the object at three points and measuring the forces, F1, F2, and F3 that resist the weight of the object, ( is the unit vector in the vertical direction). Let r1, r2, and r3 be the position coordinates of the support points, then the coordinates R of the center of mass satisfy the condition that the resultant torque is zero, or This equation yields the coordinates of the center of mass R* in the horizontal plane as, The center of mass lies on the vertical line L, given by The three-dimensional coordinates of the center of mass are determined by performing this experiment twice with the object positioned so that these forces are measured for two different horizontal planes through the object. The center of mass will be the intersection of the two lines L1 and L2 obtained from the two experiments.Applications
Engineering designs
Automotive applications
Engineers try to design a sports car so that its center of mass is lowered to make the car handle better, which is to say, maintain traction while executing relatively sharp turns. The characteristic low profile of the U.S. military Humvee was designed in part to allow it to tilt farther than taller vehicles without rolling over, by ensuring its low center of mass stays over the space bounded by the four wheels even at angles far from thehorizontal
Horizontal may refer to:
*Horizontal plane, in astronomy, geography, geometry and other sciences and contexts
*Horizontal coordinate system, in astronomy
*Horizontalism, in monetary circuit theory
*Horizontalism, in sociology
*Horizontal market, ...
.
Aeronautics
The center of mass is an important point on an aircraft, which significantly affects the stability of the aircraft. To ensure the aircraft is stable enough to be safe to fly, the center of mass must fall within specified limits. If the center of mass is ahead of the forward limit, the aircraft will be less maneuverable, possibly to the point of being unable to rotate for takeoff or flare for landing. If the center of mass is behind the aft limit, the aircraft will be more maneuverable, but also less stable, and possibly unstable enough so as to be impossible to fly. The moment arm of the elevator will also be reduced, which makes it more difficult to recover from astalled
''Stalled'' is a 2013 British zombie comedy film directed by Christian James. It stars Dan Palmer, who also wrote the screenplay, as a man confined to a bathroom stall after zombies attack. Produced by Richard Kerrigan and Daniel Pickering, the f ...
condition.
For helicopters in hover, the center of mass is always directly below the rotorhead. In forward flight, the center of mass will move forward to balance the negative pitch torque produced by applying cyclic control to propel the helicopter forward; consequently a cruising helicopter flies "nose-down" in level flight.
Astronomy
 The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the ''barycenter''. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a
The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the ''barycenter''. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star
A star is an astronomical object comprising a luminous spheroid of plasma (physics), plasma held together by its gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked ...
, both bodies are actually orbiting a point that lies away from the center of the primary (larger) body. For example, the Moon does not orbit the exact center of the Earth, but a point on a line between the center of the Earth and the Moon, approximately 1,710 km (1,062 miles) below the surface of the Earth, where their respective masses balance. This is the point about which the Earth and Moon orbit as they travel around the Sun. If the masses are more similar, e.g., Pluto and Charon, the barycenter will fall outside both bodies.
Rigging and safety
Knowing the location of the center of gravity whenrigging
Rigging comprises the system of ropes, cables and chains, which support a sailing ship or sail boat's masts—''standing rigging'', including shrouds and stays—and which adjust the position of the vessel's sails and spars to which they are ...
is crucial, possibly resulting in severe injury or death if assumed incorrectly. A center of gravity that is at or above the lift point will most likely result in a tip-over incident. In general, the further the center of gravity below the pick point, the more safe the lift. There are other things to consider, such as shifting loads, strength of the load and mass, distance between pick points, and number of pick points. Specifically, when selecting lift points, it's very important to place the center of gravity at the center and well below the lift points.
Body motion
In kinesiology and biomechanics, the center of mass is an important parameter that assists people in understanding their human locomotion. Typically, a human's center of mass is detected with one of two methods: the reaction board method is a static analysis that involves the person lying down on that instrument, and use of theirstatic equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero ...
equation to find their center of mass; the segmentation method relies on a mathematical solution based on the physical principle that the summation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, mat ...
of the torques of individual body sections, relative to a specified axis, must equal the torque of the whole system that constitutes the body, measured relative to the same axis.
See also
* Barycenter * Buoyancy * Center of mass (relativistic) *Center of percussion The center of percussion is the point on an extended massive object attached to a pivot where a perpendicular impact will produce no reactive shock at the pivot. Translational and rotational motions cancel at the pivot when an impulsive blow is st ...
* Center of pressure (fluid mechanics)
* Center of pressure (terrestrial locomotion)
* Centroid
* Circumcenter of mass
* Expected value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a l ...
* Mass point geometry
* Metacentric height
* Roll center
The roll center of a vehicle is the notional point at which the cornering forces in the suspension are reacted to the vehicle body.
There are two definitions of roll center. The most commonly used is the geometric (or kinematic) roll center, wher ...
* Weight distribution
Notes
References
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *External links
Motion of the Center of Mass
shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
simulations showing the effect each planet contributes to the Solar System's barycenter. {{DEFAULTSORT:Center Of Mass Classical mechanics Mass Mass Moment (physics)