graph theory In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conne ...

, a book embedding is a generalization of

planar embedding In graph theory, a planar graph is a graph (discrete mathematics), graph that can be graph embedding, embedded in the plane (geometry), plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. I ...

of a

graph Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties *Graph (topology), a topological space resembling a graph in the sense of discre ...

to embeddings into a ''book'', a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the ''spine'', and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other

graph invariant Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties * Graph (topology), a topological space resembling a graph in the sense of discr ...

s including the pagewidth and book crossing number. Every graph with vertices has book thickness at most

\lceil n/2\rceil

, and this formula gives the exact book thickness for

complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is ...

s. The graphs with book thickness one are the

outerplanar graph In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing. Outerplanar graphs may be characterized (analogously to Wagner's theorem for planar graphs) by the two fo ...

s. The graphs with book thickness at most two are the subhamiltonian graphs, which are always

planar Planar is an adjective meaning "relating to a plane (geometry)". Planar may also refer to: Science and technology * Planar (computer graphics), computer graphics pixel information from several bitplanes * Planar (transmission line technologies), ...

; more generally, every planar graph has book thickness at most four. All minor-closed graph families, and in particular the graphs with bounded

treewidth In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The gra ...

or bounded

genus Genus ( plural genera ) is a taxonomic rank used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In the hierarchy of biological classification, genus com ...

, also have bounded book thickness. It is

NP-hard In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard pr ...

to determine the exact book thickness of a given graph, with or without knowing a fixed vertex ordering along the spine of the book. Testing the existence of a three-page book embedding of a graph, given a fixed ordering of the vertices along the spine of the embedding, has unknown computational complexity: it is neither known to be solvable in polynomial time nor known to be NP-hard. One of the original motivations for studying book embeddings involved applications in

VLSI Very large-scale integration (VLSI) is the process of creating an integrated circuit (IC) by combining millions or billions of MOS transistors onto a single chip. VLSI began in the 1970s when MOS integrated circuit (Metal Oxide Semiconductor) c ...

design, in which the vertices of a book embedding represent components of a circuit and the wires represent connections between them. Book embedding also has applications in

graph drawing Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graph (discrete mathematics), graphs arising from applications such a ...

, where two of the standard visualization styles for graphs, arc diagrams and

circular layout In graph drawing, a circular layout is a style of drawing that places the vertices of a graph on a circle, often evenly spaced so that they form the vertices of a regular polygon. Applications Circular layouts are a good fit for communications ...

s, can be constructed using book embeddings. In

transportation planning Transportation planning is the process of defining future policies, goals, investments, and spatial planning designs to prepare for future needs to move people and goods to destinations. As practiced today, it is a collaborative process that ...

, the different sources and destinations of foot and vehicle traffic that meet and interact at a

traffic light Traffic lights, traffic signals, or stoplights – known also as robots in South Africa are signalling devices positioned at intersection (road), road intersections, pedestrian crossings, and other locations in order to control flows of traf ...

can be modeled mathematically as the vertices of a graph, with edges connecting different source-destination pairs. A book embedding of this graph can be used to design a schedule that lets all the traffic move across the intersection with as few signal phases as possible. In

bioinformatics Bioinformatics () is an interdisciplinary field that develops methods and software tools for understanding biological data, in particular when the data sets are large and complex. As an interdisciplinary field of science, bioinformatics combi ...

problems involving the folding structure of

RNA Ribonucleic acid (RNA) is a polymeric molecule essential in various biological roles in coding, decoding, regulation and expression of genes. RNA and deoxyribonucleic acid ( DNA) are nucleic acids. Along with lipids, proteins, and carbohydra ...

, single-page book embeddings represent classical forms of

nucleic acid secondary structure Nucleic acid secondary structure is the basepairing interactions within a single nucleic acid polymer or between two polymers. It can be represented as a list of bases which are paired in a nucleic acid molecule. The secondary structures of bi ...

, and two-page book embeddings represent pseudoknots. Other applications of book embeddings include

abstract algebra In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras over a field. The term ''a ...

and

knot theory In the mathematical field of topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are ...

History

The notion of a book, as a topological space, was defined by C. A. Persinger and Gail Atneosen in the 1960s.. See also . As part of this work, Atneosen already considered embeddings of graphs in books. The embeddings he studied used the same definition as embeddings of graphs into any other topological space: vertices are represented by distinct points, edges are represented by curves, and the only way that two edges can intersect is for them to meet at a common endpoint. In the early 1970s, Paul C. Kainen and L. Taylor Ollmann developed a more restricted type of embedding that came to be used in most subsequent research. In their formulation, the graph's vertices must be placed along the spine of the book, and each edge must lie in a single page. Important milestones in the later development of book embeddings include the proof by

Mihalis Yannakakis Mihalis Yannakakis ( el, Μιχάλης Γιαννακάκης; born 13 September 1953 in Athens, Greece)planar graphs have book thickness at most four, and the discovery in the late 1990s of close connections between book embeddings and

Definitions

A book is a particular kind of

topological space In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called po ...

, also called a fan of half-planes... It consists of a single line , called the spine or back of the book, together with a collection of one or more half-planes, called the pages or leaves of the book, each having the spine as its boundary. Books with a

finite number Finite number may refer to: * A countable number less than infinity, being the cardinality of a finite set – i.e., some natural number, possibly 0 * A real number In mathematics, a real number is a number that can be used to measure a ''cont ...

of pages can be embedded into three-dimensional space, for instance by choosing to be the -axis of a Cartesian coordinate system and choosing the pages to be the half-planes whose

dihedral angle A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the un ...

with respect to the -plane is an integer multiple of . A book drawing of a finite graph onto a book is a

drawing Drawing is a form of visual art in which an artist uses instruments to mark paper or other two-dimensional surface. Drawing instruments include graphite pencils, pen and ink, various kinds of paints, inked brushes, colored pencils, crayons, ...

of on such that every vertex of is drawn as a point on the spine of , and every edge of is drawn as a

curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...

that lies within a single page of . The -page book crossing number of is the minimum number of crossings in a -page book drawing.. A book embedding of onto is a book drawing that forms a

graph embedding In topological graph theory, an embedding (also spelled imbedding) of a graph G on a surface \Sigma is a representation of G on \Sigma in which points of \Sigma are associated with vertices and simple arcs (homeomorphic images of ,1/math> ...

of into . That is, it is a book drawing of on that does not have any edge crossings. Every finite graph has a book embedding onto a book with a large enough number of pages. For instance, it is always possible to embed each edge of the graph on its own separate page. The book thickness, pagenumber, or stack number of is the minimum number of pages required for a book embedding of . Another parameter that measures the quality of a book embedding, beyond its number of pages, is its pagewidth. This is the maximum number of edges that can be crossed by a ray perpendicular to the spine within a single page. Equivalently (for book embeddings in which each edge is drawn as a monotonic curve), it is the maximum size of a subset of edges within a single page such that the

intervals Interval may refer to: Mathematics and physics * Interval (mathematics), a range of numbers ** Partially ordered set#Intervals, its generalization from numbers to arbitrary partially ordered sets * A statistical level of measurement * Interval e ...

defined on the spine by pairs of endpoints of the edges all intersect each other. It is crucial for these definitions that edges are only allowed to stay within a single page of the book. As Atneosen already observed, if edges may instead pass from one page to another across the spine of the book, then every graph may be embedded into a three-page book. For such a three-page topological book embedding in which spine crossings are allowed, every graph can be embedded with at most a logarithmic number of spine crossings per edge,. and some graphs need this many spine crossings.

Specific graphs

As shown in the first figure, the book thickness of the

is three: as a non-planar graph its book thickness is greater than two, but a book embedding with three pages exists. More generally, the book thickness of every complete graph with vertices is exactly

\lceil n/2\rceil

. This result also gives an

upper bound In mathematics, particularly in order theory, an upper bound or majorant of a subset of some preordered set is an element of that is greater than or equal to every element of . Dually, a lower bound or minorant of is defined to be an eleme ...

on the maximum possible book thickness of any -vertex graph. The two-page crossing number of the complete graph is :

\frac \biggl\lfloor\frac\biggr\rfloor\biggl\lfloor\frac\biggr\rfloor\biggl\lfloor\frac\biggr\rfloor\biggl\lfloor\frac\biggr\rfloor,

matching a still-unproven conjecture of Anthony Hill on what the unrestricted crossing number of this graph should be. That is, if Hill's conjecture is correct, then the drawing of this graph that minimizes the number of crossings is a two-page drawing. The book thickness of the

complete bipartite graph In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set..Electronic edition page 17. Graph theory i ...

is at most . To construct a drawing with this book thickness, for each vertex on the smaller side of the bipartition, one can place the edges incident with that vertex on their own page. This bound is not always tight; for instance, has book thickness three, not four. However, when the two sides of the graph are very unbalanced, with , the book thickness of is exactly . For the

Turán graph The Turán graph, denoted by T(n,r), is a complete multipartite graph; it is formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and then connecting two vertices by an edge if and only if they belong to di ...

complete multipartite graph In graph theory, a part of mathematics, a -partite graph is a graph whose vertices are (or can be) partitioned into different independent sets. Equivalently, it is a graph that can be colored with colors, so that no two endpoints of an edge ...

formed from independent sets of vertices per independent set, with an edge between every two vertices from different independent sets) the book thickness is sandwiched between :

\left\lceil \frac\right\rceil \le t \le \left\lceil \frac \right\rceil

and when is odd the upper bound can be improved to :

t\le (r-1)\left\lceil\frac\right\rceil + \left\lceil \frac \right\rceil.

The book thickness of binary

de Bruijn graph In graph theory, an -dimensional De Bruijn graph of symbols is a directed graph representing overlaps between sequences of symbols. It has vertices, consisting of all possible sequences of the given symbols; the same symbol may appear multiple ...

s, shuffle-exchange graphs, and

cube-connected cycles In graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by for use as a network topology in parallel computing. Definition The cube-connected c ...

(when these graphs are large enough to be nonplanar) is exactly three.

Properties

Planarity and outerplanarity

The book thickness of a given graph is at most one if and only if is an

. An outerplanar graph is a graph that has a planar embedding in which all vertices belong to the outer face of the embedding. For such a graph, placing the vertices in the same order along the spine as they appear in the outer face provides a one-page book embedding of the given graph. (An

articulation point Articulation may refer to: Linguistics * Articulatory phonetics, the study of how humans produce speech sounds via the interaction of physiological structures ** Manner of articulation, how speech organs involved in making a sound make contact * ...

of the graph will necessarily appear more than once in the cyclic ordering of vertices around the outer face, but only one of those copies should be included in the book embedding.) Conversely, a one-page book embedding is automatically an outerplanar embedding. For, if a graph is embedded on a single page, and another half-plane is attached to the spine to extend its page to a complete plane, then the outer face of the embedding includes the entire added half-plane, and all vertices lie on this outer face. Every two-page book embedding is a special case of a planar embedding, because the union of two pages of a book is a space topologically equivalent to the whole plane. Therefore, every graph with book thickness two is automatically a planar graph. More precisely, the book thickness of a graph is at most two if and only if is a subgraph of a planar graph that has a

Hamiltonian cycle In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex ...

.. If a graph is given a two-page embedding, it can be augmented to a planar Hamiltonian graph by adding (into any page) extra edges between any two consecutive vertices along the spine that are not already adjacent, and between the first and last spine vertices. The

Goldner–Harary graph In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal ...

provides an example of a planar graph that does not have book thickness two: it is a

maximal planar graph In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cros ...

, so it is not possible to add any edges to it while preserving planarity, and it does not have a Hamiltonian cycle. Because of this characterization by Hamiltonian cycles, graphs that have two-page book embeddings are also known as subhamiltonian graphs.. All planar graphs whose maximum degree is at most four have book thickness at most two.. Planar 3-trees have book thickness at most three.. More generally, all planar graphs have book thickness four. It has been claimed by

Mihalis Yannakakis Mihalis Yannakakis ( el, Μιχάλης Γιαννακάκης; born 13 September 1953 in Athens, Greece). that there exist some planar graphs that have book thickness exactly four. However, a detailed proof of this claim, announced in a subsequent journal paper, was not known until 2020, when Bekos et al.. presented planar graphs with

4 that require four pages in any book embedding.

Behavior under subdivisions

Subdividing every edge of a graph into two-edge paths, by adding new vertices within each edge, may sometimes increase its book thickness. For instance, the

diamond graph In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges. It consists of a complete graph minus one edge. The diamond graph has radius 1, diameter 2, girth 3, chroma ...

has book thickness one (it is outerplanar) but its subdivision has book thickness two (it is planar and subhamiltonian but not outerplanar). However, this subdivision process can also sometimes significantly reduce the book thickness of the subdivided graph. For instance, the book thickness of the

is proportional to its number of vertices, but subdividing each of its edges into a two-edge path produces a subdivision whose book thickness is much smaller, only

O(\sqrt n)

.. Despite the existence of examples such as this one, conjectured that a subdivision's book thickness cannot be too much smaller than that of the original graph. Specifically, they conjectured that there exists a function such that, for every graph and for the graph formed by replacing every edge in by a two-edge path, if the book thickness of is then the book thickness of is at most .. Their conjecture turned out to be false: graphs formed by Cartesian products of

stars A star is an astronomical object comprising a luminous spheroid of plasma held together by its gravity. The nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night, but their immense distances from Earth ma ...

and

triangular tiling In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilate ...

s have unbounded book thickness, but subdividing their edges into six-edge paths reduces their book thickness to three.

Relation to other graph invariants

Book thickness is related to

thickness Thickness may refer to: * Thickness (graph theory) * Thickness (geology), the distance across a layer of rock * Thickness (meteorology), the difference in height between two atmospheric pressure levels * Thickness planer a woodworking machine ...

, the number of planar graphs needed to cover the edges of the given graph. A graph has thickness if it can be drawn in the plane, and its edges

colored ''Colored'' (or ''coloured'') is a racial descriptor historically used in the United States during the Jim Crow, Jim Crow Era to refer to an African Americans, African American. In many places, it may be considered a Pejorative, slur, though it ...

with colors, in such a way that edges of the same color as each other do not cross. Analogously, a graph has book thickness if it can be drawn in a

half plane In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional Euclidean space. If the space is two-dimensional, then a half-space is called a half-plane (open or closed). A half-space in a one-dimensional ...

, with its vertices on the boundary of the half plane, with its edges colored with colors with no crossing between two edges of the same color. In this formulation of book thickness, the colors of the edges correspond to the pages of the book embedding. However, thickness and book thickness can be very different from each other: there exist graphs (

subdivisions Subdivision may refer to: Arts and entertainment * Subdivision (metre), in music * ''Subdivision'' (film), 2009 * "Subdivision", an episode of ''Prison Break'' (season 2) * ''Subdivisions'' (EP), by Sinch, 2005 * "Subdivisions" (song), by Rush ...

s) that have unbounded book thickness, despite having thickness two. Graphs of

have book thickness at most . and this bound is tight for . Graphs with edges have book thickness

O(\sqrt m)

, and graphs of

have book thickness

O(\sqrt g)

. More generally, every minor-closed graph family has bounded book thickness.. On the other hand, the 1-planar graphs, which are not closed under minors, have also bounded book thickness, but some 1-planar graphs including have book thickness at least four.. Every shallow minor of a graph of bounded book thickness is a

sparse graph In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges (where every pair of vertices is connected by one edge). The opposite, a graph with only a few edges, is a sparse graph. The distinction ...

, whose ratio of edges to vertices is bounded by a constant that depends only on the depth of the minor and on the book thickness. That is, in the terminology of , the graphs of bounded book thickness have

bounded expansion In graph theory, a family of graphs is said to have bounded expansion if all of its shallow minors are sparse graphs. Many natural families of sparse graphs have bounded expansion. A closely related but stronger property, polynomial expansion, ...

. However, even the graphs of bounded

degree Degree may refer to: As a unit of measurement * Degree (angle), a unit of angle measurement ** Degree of geographical latitude ** Degree of geographical longitude * Degree symbol (°), a notation used in science, engineering, and mathematics ...

, a much stronger requirement than having bounded expansion, can have unbounded book thickness. Because graphs of book thickness two are planar graphs, they obey the

planar separator theorem In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of verti ...

: they have separators, subsets of vertices whose removal splits the graph into pieces with at most vertices each, with only

O(\sqrt n)

vertices in the separator. Here, refers to the number of vertices in the graph. However, there exist graphs of book thickness three that do not have separators of sublinear size., improving an earlier result showing the existence of expanders with constant pagenumber from ; . See also ; . The edges within a single page of a book embedding behave in some ways like a stack data structure. This can be formalized by considering an arbitrary sequence of push and pop operations on a stack, and forming a graph in which the stack operations correspond to the vertices of the graph, placed in sequence order along the spine of a book embedding. Then, if one draws an edge from each pop operation that pops an object from the stack, to the previous push operation that pushed , the resulting graph will automatically have a one-page embedding. For this reason, the page number of a graph has also been called its stack number. In the same way, one may consider an arbitrary sequence of enqueue and dequeue operations of a queue data structure, and form a graph that has these operations as its vertices, placed in order on the spine of a single page, with an edge between each enqueue operation and the corresponding dequeue. Then, in this graph, each two edges will either cross or cover disjoint intervals on the spine. By analogy, researchers have defined a queue embedding of a graph to be an embedding in a topological book such that each vertex lies on the spine, each edge lies in a single page, and each two edges in the same page either cross or cover disjoint intervals on the spine. The minimum number of pages needed for a queue embedding of a graph is called its

queue number In the mathematical field of graph theory, the queue number of a graph is a graph invariant defined analogously to stack number (book thickness) using first-in first-out (queue) orderings in place of last-in first-out (stack) orderings. Defi ...

Computational complexity

Finding the book thickness of a graph is

. This follows from the fact that finding Hamiltonian cycles in maximal planar graphs is

NP-complete In computational complexity theory, a problem is NP-complete when: # it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by tryi ...

. In a maximal planar graph, the book thickness is two if and only if a Hamiltonian cycle exists. Therefore, it is also NP-complete to test whether the book thickness of a given maximal planar graph is two. If an ordering of the vertices of a graph along the spine of an embedding is fixed, then a two-page embedding (if it exists) can be found in linear time, as an instance of

planarity testing In graph theory, the planarity testing problem is the algorithmic problem of testing whether a given graph is a planar graph (that is, whether it can be drawn in the plane without edge intersections). This is a well-studied problem in computer sc ...

for a graph formed by augmenting the given graph with a cycle connecting the vertices in their spine ordering. claimed that finding three-page embeddings with a fixed spine ordering can also be performed in

polynomial time In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by ...

although his writeup of this result omits many details.. However, for graphs that require four or more pages, the problem of finding an embedding with the minimum possible number of pages remains NP-hard, via an equivalence to the NP-hard problem of coloring circle graphs, the

intersection graph In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types o ...

s of

chords Chord may refer to: * Chord (music), an aggregate of musical pitches sounded simultaneously ** Guitar chord a chord played on a guitar, which has a particular tuning * Chord (geometry), a line segment joining two points on a curve * Chord ( ...

of a

circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is con ...

. Given a graph with a fixed spine ordering for its vertices, drawing these vertices in the same order around a circle and drawing the edges of as line segments produces a collection of chords representing . One can then form a circle graph that has the chords of this diagram as vertices and crossing pairs of chords as edges. A coloring of the circle graph represents a partition of the edges of into subsets that can be drawn without crossing on a single page. Therefore, an optimal coloring is equivalent to an optimal book embedding. Since circle graph coloring with four or more colors is NP-hard, and since any circle graph can be formed in this way from some book embedding problem, it follows that optimal book embedding is also NP-hard... For a fixed vertex ordering on the spine of a two-page book drawing, it is also NP-hard to minimize the number of crossings when this number is nonzero. If the spine ordering is unknown but a partition of the edges into two pages is given, then it is possible to find a 2-page embedding (if it exists) in linear time by an algorithm based on

SPQR tree In graph theory, a branch of mathematics, the triconnected components of a biconnected graph are a system of smaller graphs that describe all of the 2-vertex cuts in the graph. An SPQR tree is a tree data structure used in computer science, and ...

s.. However, it is NP-complete to find a 2-page embedding when neither the spine ordering nor the edge partition is known. Finding the book crossing number of a graph is also NP-hard, because of the NP-completeness of the special case of testing whether the 2-page crossing number is zero. As a consequence of bounded expansion, the subgraph isomorphism problem, of finding whether a pattern graph of bounded size exists as a subgraph of a larger graph, can be solved in linear time when the larger graph has bounded book thickness. The same is true for detecting whether the pattern graph is an

induced subgraph In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and ''all'' of the edges (from the original graph) connecting pairs of vertices in that subset. Defini ...

of the larger graph, or whether it has a

graph homomorphism In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent verti ...

to the larger graph. For the same reason, the problem of testing whether a graph of bounded book thickness obeys a given formula of

first order logic First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantifie ...

fixed-parameter tractable In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to ''multiple'' parameters of the input or output. T ...

. describe a system for finding optimal book embeddings by transforming the problem into an instance of the

Boolean satisfiability problem In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfie ...

and applying a SAT solver to the resulting problem. They state that their system is capable of finding an optimal embedding for 400-vertex

s in approximately 20 minutes.

Applications

Fault-tolerant multiprocessing

One of the main motivations for studying book embedding cited by involves an application in

design, to the organization of

fault-tolerant Fault tolerance is the property that enables a system to continue operating properly in the event of the failure of one or more faults within some of its components. If its operating quality decreases at all, the decrease is proportional to the ...

multiprocessor Multiprocessing is the use of two or more central processing units (CPUs) within a single computer system. The term also refers to the ability of a system to support more than one processor or the ability to allocate tasks between them. There ar ...

s. In the DIOGENES system developed by these authors, the CPUs of a multiprocessor system are arranged into a logical sequence corresponding to the spine of a book (although this sequence may not necessarily be placed along a line in the

physical layout Integrated circuit layout, also known IC layout, IC mask layout, or mask design, is the representation of an integrated circuit in terms of planar geometric shapes which correspond to the patterns of metal, oxide, or semiconductor layers that make ...

of this system). Communication links connecting these processors are grouped into "bundles" which correspond to the pages of a book and act like stacks: connecting one of the processors to the start of a new communications link pushes all the previous links upward in the bundle, and connecting another processor to the end of a communication link connects it to the one at the bottom of the bundle and pops all the other ones down. Because of this stack behavior, a single bundle can handle a set of communications links that form the edges of a single page in a book embedding. By organizing the links in this way, a wide variety of different network topologies can be implemented, regardless of which processors have become faulty, as long as enough non-faulty processors remain to implement the network. The network topologies that can be implemented by this system are exactly the ones that have book thickness at most equal to the number of bundles that have been made available.. Book embedding may also be used to model the placement of wires connecting VLSI components into the layers of a circuit.

Stack sorting

Another application cited by concerns sorting permutations using stacks. An influential result of showed that a system that processes a

data stream In connection-oriented communication, a data stream is the transmission of a sequence of digitally encoded coherent signals to convey information. Typically, the transmitted symbols are grouped into a series of packets. Data streaming has b ...

by pushing incoming elements onto a stack and then, at appropriately chosen times, popping them from the stack onto an output stream can

sort Sort may refer to: * Sorting, any process of arranging items in sequence or in sets ** Sorting algorithm, any algorithm for arranging elements in lists ** Sort (Unix), a Unix utility which sorts the lines of a file ** Sort (C++), a function in the ...

the data if and only if its initial order is described by a permutation that avoids the

permutation pattern In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of digits representing the result of applying the p ...

231. Since then, there has been much work on similar problems of sorting data streams by more general systems of stacks and queues. In the system considered by , each element from an input data stream must be pushed onto one of several stacks. Then, once all of the data has been pushed in this way, the items are popped from these stacks (in an appropriate order) onto an output stream. As Chung et al. observe, a given permutation can be sorted by this system if and only if a certain graph, derived from the permutation, has a book embedding with the vertices in a certain fixed order along the spine and with a number of pages that is at most equal to the number of stacks.

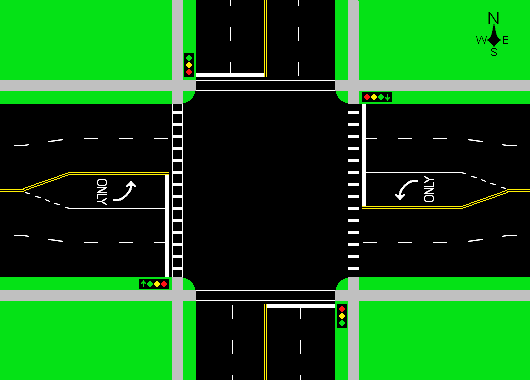
Traffic control

As described, a book embedding may be used to describe the phases of a

traffic signal Traffic lights, traffic signals, or stoplights – known also as robots in South Africa are signalling devices positioned at road intersections, pedestrian crossings, and other locations in order to control flows of traffic. Traffic light ...

at a controlled intersection. At an intersection, the incoming and outgoing lanes of traffic (including the ends of pedestrian crosswalks and bicycle lanes as well as lanes for motor vehicles) may be represented as the vertices of a graph, placed on the spine of a book embedding in their clockwise order around the junction. The paths through the intersection taken by traffic to get from an incoming lane to an outgoing lane may be represented as the edges of an undirected graph. For instance, this graph might have an edge from an incoming to an outgoing lane of traffic that both belong to the same segment of road, representing a U-turn from that segment back to that segment, only if U-turns are allowed at the junction. For a given subset of these edges, the subset represents a collection of paths that can all be traversed without interference from each other if and only if the subset does not include any pair of edges that would cross if the two edges were placed in a single page of a book embedding. Thus, a book embedding of this graph describes a partition of the paths into non-interfering subsets, and the book thickness of this graph (with its fixed embedding on the spine) gives the minimum number of distinct phases needed for a signalling schedule that includes all possible traffic paths through the junction..

Graph drawing

Book embedding has also been frequently applied in the visualization of network data. Two of the standard layouts in

, arc diagrams and circular layouts, can be viewed as book embeddings, and book embedding has also been applied in the construction of clustered layouts, simultaneous embeddings, and three-dimensional graph drawings. An arc diagram. or linear embedding places vertices of a graph along a line, and draws the edges of the graph as semicircles either above or below this line, sometimes also allowing edges to be drawn on segments of the line. This drawing style corresponds to a book embedding with either one page (if all semicircles are above the line) or two pages (if both sides of the line are used), and was originally introduced as a way of studying the crossing numbers of graphs. Planar graphs that do not have two-page book embeddings may also be drawn in a similar way, by allowing their edges to be represented by multiple semicircles above and below the line. Such a drawing is not a book embedding by the usual definition, but has been called a topological book embedding. For every planar graph, it is always possible to find such an embedding in which each edge crosses the spine at most once. Chvatal Lombardi

In another drawing style, the

, the vertices of a graph are placed on a circle and the edges are drawn either inside or outside the circle.. Again, a placement of the edges within the circle (for instance as straight line segments) corresponds to a one-page book drawing, while a placement both inside and outside the circle corresponds to a two-page book drawing. For one-page drawings of either style, it is important to keep the number of crossings small as a way of reducing the visual clutter of the drawing. Minimizing the number of crossings is

, but may be approximated with an approximation ratio of where is the number of vertices. Minimizing the one-page or two-page crossing number is

when parameterized by the

cyclomatic number In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or fo ...

of the given graph, or by a combination of the crossing number and the

of the graph. Heuristic methods for reducing the crossing complexity have also been devised, based e.g. on a careful vertex insertion order and on local optimization. Two-page book embeddings with a fixed partition of the edges into pages can be interpreted as a form of

clustered planarity In graph drawing, a clustered planar graph is a graph together with a hierarchical clustering on its vertices, such that the graph drawn together with a collection of simple closed curves surrounding each cluster, so that there are no crossings be ...

, in which the given graph must be drawn in such a way that parts of the graph (the two subsets of edges) are placed in the drawing in a way that reflects their clustering. Two-page book embedding has also been used to find

simultaneous embedding Simultaneous embedding is a technique in graph drawing and information visualization for visualizing two or more different graphs on the same or overlapping sets of labeled vertices, while avoiding crossings within both graphs. Crossings between ...

s of graphs, in which two graphs are given on the same vertex set and one must find a placement for the vertices in which both graphs are drawn planarly with straight edges.. Book embeddings with more than two pages have also been used to construct three-dimensional drawings of graphs. In particular, used a construction for book embeddings that keep the

of each vertex within each page low, as part of a method for embedding graphs into a three-dimensional grid of low volume..

RNA folding

In the study of how

molecules fold to form their structure, the standard form of

can be described diagrammatically as a chain of bases (the RNA sequence itself), drawn along a line, together with a collection of arcs above the line describing the basepairs of the structure. That is, although these structures actually have a complicated three-dimensional shape, their connectivity (when a secondary structure exists) can be described by a more abstract structure, a one-page book embedding. However, not all RNA folds behave in this simple way. have proposed a so-called "bi-secondary structure" for certain RNA pseudoknots that takes the form of a two-page book embedding: the RNA sequence is again drawn along a line, but the basepairs are drawn as arcs both above and below this line. In order to form a bi-secondary structure, a graph must have maximum degree at most three: each base can only participate in one arc of the diagram, in addition to the two links to its neighbors in the base sequence. Advantages of this formulation include the facts that it excludes structures that are actually knotted in space, and that it matches most known RNA pseudoknots.. Because the spine ordering is known in advance for this application, testing for the existence of a bi-secondary structure for a given basepairing is straightforward. The problem of assigning edges to the two pages in a compatible way can be formulated as either an instance of 2-satisfiability, or as a problem of testing the bipartiteness of the circle graph whose vertices are the basepairs and whose edges describe crossings between basepairs. Alternatively and more efficiently, as show, a bi-secondary structure exists if and only if the ''diagram graph'' of the input (a graph formed by connecting the bases into a cycle in their sequence order and adding the given basepairs as edges) is a planar graph. This characterization allows bi-secondary structures to be recognized in linear time as an instance of

. used the connection between secondary structures and book embeddings as part of a proof of the

ness of certain problems in RNA secondary structure comparison. And if an RNA structure is tertiary rather than bi-secondary (that is, if it requires more than two pages in its diagram), then determining the page number is again NP-hard.

Computational complexity theory

used book embedding to study the

computational complexity theory In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by ...

of the

reachability In graph theory, reachability refers to the ability to get from one Vertex (graph theory), vertex to another within a graph. A vertex s can reach a vertex t (and t is reachable from s) if there exists a sequence of Glossary of graph theory#Basics, ...

problem in

directed graph In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pa ...

s. As they have observed, reachability for two-page directed graphs may be solved in unambiguous logarithmic space (the analogue, for logarithmic space complexity, of the class UP of unambiguous polynomial-time problems). However, reachability for three-page directed graphs requires the full power of nondeterministic logarithmic space. Thus, book embeddings seem intimately connected with the distinction between these two complexity classes. The existence of

expander graph In graph theory, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion. Expander constructions have spawned research in pure and applied mathematics, with several applica ...

s with constant page number is the key step in proving that there is no subquadratic-time simulation of two-tape

non-deterministic Turing machine In theoretical computer science, a nondeterministic Turing machine (NTM) is a theoretical model of computation whose governing rules specify more than one possible action when in some given situations. That is, an NTM's next state is ''not'' comp ...

s by one-tape non-deterministic Turing machines..

Other areas of mathematics

study applications of book thickness in

, using graphs defined from the

zero divisor In abstract algebra, an element of a ring is called a left zero divisor if there exists a nonzero in such that , or equivalently if the map from to that sends to is not injective. Similarly, an element of a ring is called a right zer ...

s of a finite

local ring In abstract algebra, more specifically ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic n ...

by making a vertex for each zero divisor and an edge for each pair of values whose product is zero.. In a multi-paper sequence, Dynnikov has studied the topological book embeddings of

knots A knot is a fastening in rope or interwoven lines. Knot may also refer to: Places * Knot, Nancowry, a village in India Archaeology * Knot of Isis (tyet), symbol of welfare/life. * Minoan snake goddess figurines#Sacral knot Arts, entertainme ...

and links, showing that these embeddings can be described by a combinatorial sequence of symbols and that the topological equivalence of two links can be demonstrated by a sequence of local changes to the embeddings...

References

{{reflist, 30em Topological graph theory