Binary search tree on:
[Wikipedia]
[Google]
[Amazon]
 In
In
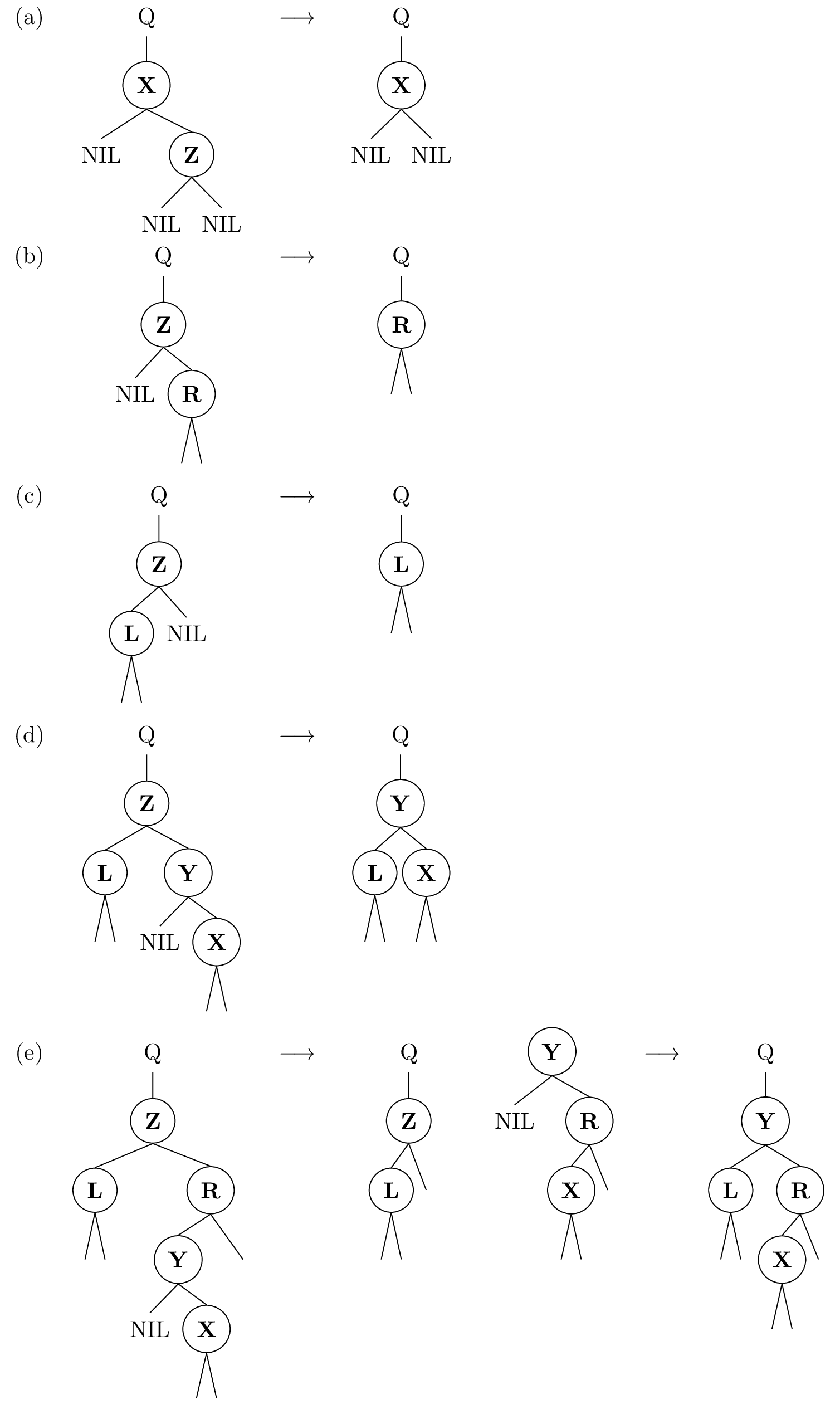 The deletion of a node, say , from the binary search tree has three cases:
# If is a leaf node, it is replaced by as shown in (a).
# If has only one child, the child node of gets elevated by modifying the parent node of to point to the child node, consequently taking 's position in the tree, as shown in (b) and (c).
# If has both left and right children, the in-order successor of , say , displaces by following the two cases:
## If is 's right child, as shown in (d), displaces and 's right child remain unchanged.
## If lies within 's right subtree but is not 's right child, as shown in (e), first gets replaced by its own right child, and then it displaces 's position in the tree.
# Alternatively, the in-order predecessor can also be used.
The following pseudocode implements the deletion operation in a binary search tree.
The procedure deals with the 3 special cases mentioned above. Lines 2-3 deal with case 1; lines 4-5 deal with case 2 and lines 6-16 for case 3. The helper function is used within the deletion algorithm for the purpose of replacing the node with in the binary search tree . This procedure handles the deletion (and substitution) of from .
The deletion of a node, say , from the binary search tree has three cases:
# If is a leaf node, it is replaced by as shown in (a).
# If has only one child, the child node of gets elevated by modifying the parent node of to point to the child node, consequently taking 's position in the tree, as shown in (b) and (c).
# If has both left and right children, the in-order successor of , say , displaces by following the two cases:
## If is 's right child, as shown in (d), displaces and 's right child remain unchanged.
## If lies within 's right subtree but is not 's right child, as shown in (e), first gets replaced by its own right child, and then it displaces 's position in the tree.
# Alternatively, the in-order predecessor can also be used.
The following pseudocode implements the deletion operation in a binary search tree.
The procedure deals with the 3 special cases mentioned above. Lines 2-3 deal with case 1; lines 4-5 deal with case 2 and lines 6-16 for case 3. The helper function is used within the deletion algorithm for the purpose of replacing the node with in the binary search tree . This procedure handles the deletion (and substitution) of from .
''An Introduction to Binary Search Trees and Balanced Trees''.
(PDF; 1675 kB) 2004.
Binary Tree Visualizer
(JavaScript animation of various BT-based data structures) {{DEFAULTSORT:Binary search tree Articles with example C++ code Articles with example Python (programming language) code Binary trees Search trees
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
data structure
In computer science, a data structure is a data organization and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the relationships amo ...
with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations ...
of operations on the binary search tree is linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
with respect to the height of the tree.
Binary search trees allow binary search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the m ...
for fast lookup, addition, and removal of data items. Since the nodes in a BST are laid out so that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm
In mathematics, the binary logarithm () is the exponentiation, power to which the number must be exponentiation, raised to obtain the value . That is, for any real number ,
:x=\log_2 n \quad\Longleftrightarrow\quad 2^x=n.
For example, th ...
. BSTs were devised in the 1960s for the problem of efficient storage of labeled data and are attributed to Conway Berners-Lee and David Wheeler.
The performance of a binary search tree is dependent on the order of insertion of the nodes into the tree since arbitrary insertions may lead to degeneracy; several variations of the binary search tree can be built with guaranteed worst-case performance. The basic operations include: search, traversal, insert and delete. BSTs with guaranteed worst-case complexities perform better than an unsorted array, which would require linear search time.
The complexity analysis of BST shows that, on average, the insert, delete and search takes for nodes. In the worst case, they degrade to that of a singly linked list: . To address the boundless increase of the tree height with arbitrary insertions and deletions, self-balancing variants of BSTs are introduced to bound the worst lookup complexity to that of the binary logarithm. AVL trees were the first self-balancing binary search trees, invented in 1962 by Georgy Adelson-Velsky and Evgenii Landis.
Binary search trees can be used to implement abstract data type
In computer science, an abstract data type (ADT) is a mathematical model for data types, defined by its behavior (semantics) from the point of view of a '' user'' of the data, specifically in terms of possible values, possible operations on data ...
s such as dynamic sets, lookup table
In computer science, a lookup table (LUT) is an array data structure, array that replaces runtime (program lifecycle phase), runtime computation of a mathematical function (mathematics), function with a simpler array indexing operation, in a proc ...
s and priority queues, and used in sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a List (computing), list into an Total order, order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending ...
s such as tree sort.
History
The binary search tree algorithm was discovered independently by several researchers, including P.F. Windley,Andrew Donald Booth
Andrew Donald Booth (11 February 1918 – 29 November 2009)
, Andrew Colin, Thomas N. Hibbard. The algorithm is attributed to Conway Berners-Lee and David Wheeler, who used it for storing labeled data in magnetic tape
Magnetic tape is a medium for magnetic storage made of a thin, magnetizable coating on a long, narrow strip of plastic film. It was developed in Germany in 1928, based on the earlier magnetic wire recording from Denmark. Devices that use magnetic ...
s in 1960. One of the earliest and popular binary search tree algorithm is that of Hibbard.
The time complexity of a binary search tree increases boundlessly with the tree height if the nodes are inserted in an arbitrary order, therefore self-balancing binary search tree
In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height (maximal number of levels below the root) small in the face of arbitrary item insertions and deletions.Donald ...
s were introduced to bound the height of the tree to . Various height-balanced binary search trees were introduced to confine the tree height, such as AVL tree
In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by m ...
s, Treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of i ...
s, and red–black trees.
The AVL tree was invented by Georgy Adelson-Velsky and Evgenii Landis in 1962 for the efficient organization of information. It was the first self-balancing binary search tree to be invented.
Overview
A binary search tree is a rooted binary tree in which nodes are arranged instrict total order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X:
# a \leq a ( ref ...
in which the nodes with keys greater than any particular node ''A'' is stored on the right sub-trees to that node ''A'' and the nodes with keys equal to or less than ''A'' are stored on the left sub-trees to ''A,'' satisfying the binary search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the m ...
property.
Binary search trees are also efficacious in sorting
Sorting refers to ordering data in an increasing or decreasing manner according to some linear relationship among the data items.
# ordering: arranging items in a sequence ordered by some criterion;
# categorizing: grouping items with similar p ...
s and search algorithm
In computer science, a search algorithm is an algorithm designed to solve a search problem. Search algorithms work to retrieve information stored within particular data structure, or calculated in the Feasible region, search space of a problem do ...
s. However, the search complexity of a BST depends upon the order in which the nodes are inserted and deleted; since in worst case, successive operations in the binary search tree may lead to degeneracy and form a singly linked list
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes whic ...
(or "unbalanced tree") like structure, thus has the same worst-case complexity as a linked list
In computer science, a linked list is a linear collection of data elements whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes whi ...
.
Binary search trees are also a fundamental data structure used in construction of abstract data structures such as sets, multisets
In mathematics, a multiset (or bag, or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the ''multiplicity'' of ...
, and associative array
In computer science, an associative array, key-value store, map, symbol table, or dictionary is an abstract data type that stores a collection of (key, value) pairs, such that each possible key appears at most once in the collection. In math ...
s.
Operations
Searching
Searching in a binary search tree for a specific key can be programmed recursively or iteratively. Searching begins by examining theroot node
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be co ...
. If the tree is , the key being searched for does not exist in the tree. Otherwise, if the key equals that of the root, the search is successful and the node is returned. If the key is less than that of the root, the search proceeds by examining the left subtree. Similarly, if the key is greater than that of the root, the search proceeds by examining the right subtree. This process is repeated until the key is found or the remaining subtree is . If the searched key is not found after a subtree is reached, then the key is not present in the tree.
Recursive search
The followingpseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actio ...
implements the BST search procedure through recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in m ...
.
The recursive procedure continues until a or the being searched for are encountered.
Iterative search
The recursive version of the search can be "unrolled" into awhile loop
In most computer programming languages, a while loop is a control flow Statement (computer science), statement that allows code to be executed repeatedly based on a given Boolean data type, Boolean condition. The ''while'' loop can be thought o ...
. On most machines, the iterative version is found to be more efficient.
Since the search may proceed till some leaf node, the running time complexity of BST search is where is the height of the tree. However, the worst case for BST search is where is the total number of nodes in the BST, because an unbalanced BST may degenerate to a linked list. However, if the BST is height-balanced the height is .
Successor and predecessor
For certain operations, given a node , finding the successor or predecessor of is crucial. Assuming all the keys of a BST are distinct, the successor of a node in a BST is the node with the smallest key greater than 's key. On the other hand, the predecessor of a node in a BST is the node with the largest key smaller than 's key. The following pseudocode finds the successor and predecessor of a node in a BST. Operations such as finding a node in a BST whose key is the maximum or minimum are critical in certain operations, such as determining the successor and predecessor of nodes. Following is the pseudocode for the operations.Insertion
Operations such as insertion and deletion cause the BST representation to change dynamically. The data structure must be modified in such a way that the properties of BST continue to hold. New nodes are inserted as leaf nodes in the BST. Following is an iterative implementation of the insertion operation. The procedure maintains a "trailing pointer" as a parent of . After initialization on line 2, the while loop along lines 4-11 causes the pointers to be updated. If is , the BST is empty, thus is inserted as the root node of the binary search tree , if it is not , insertion proceeds by comparing the keys to that of on the lines 15-19 and the node is inserted accordingly.Deletion
 The deletion of a node, say , from the binary search tree has three cases:
# If is a leaf node, it is replaced by as shown in (a).
# If has only one child, the child node of gets elevated by modifying the parent node of to point to the child node, consequently taking 's position in the tree, as shown in (b) and (c).
# If has both left and right children, the in-order successor of , say , displaces by following the two cases:
## If is 's right child, as shown in (d), displaces and 's right child remain unchanged.
## If lies within 's right subtree but is not 's right child, as shown in (e), first gets replaced by its own right child, and then it displaces 's position in the tree.
# Alternatively, the in-order predecessor can also be used.
The following pseudocode implements the deletion operation in a binary search tree.
The procedure deals with the 3 special cases mentioned above. Lines 2-3 deal with case 1; lines 4-5 deal with case 2 and lines 6-16 for case 3. The helper function is used within the deletion algorithm for the purpose of replacing the node with in the binary search tree . This procedure handles the deletion (and substitution) of from .
The deletion of a node, say , from the binary search tree has three cases:
# If is a leaf node, it is replaced by as shown in (a).
# If has only one child, the child node of gets elevated by modifying the parent node of to point to the child node, consequently taking 's position in the tree, as shown in (b) and (c).
# If has both left and right children, the in-order successor of , say , displaces by following the two cases:
## If is 's right child, as shown in (d), displaces and 's right child remain unchanged.
## If lies within 's right subtree but is not 's right child, as shown in (e), first gets replaced by its own right child, and then it displaces 's position in the tree.
# Alternatively, the in-order predecessor can also be used.
The following pseudocode implements the deletion operation in a binary search tree.
The procedure deals with the 3 special cases mentioned above. Lines 2-3 deal with case 1; lines 4-5 deal with case 2 and lines 6-16 for case 3. The helper function is used within the deletion algorithm for the purpose of replacing the node with in the binary search tree . This procedure handles the deletion (and substitution) of from .
Traversal
A BST can be traversed through three basic algorithms: inorder,preorder
In mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive relation, reflexive and Transitive relation, transitive. The name is meant to suggest that preorders are ''almost'' partial orders, ...
, and postorder tree walks.
*Inorder tree walk: Nodes from the left subtree get visited first, followed by the root node and right subtree. Such a traversal visits all the nodes in the order of non-decreasing key sequence.
*Preorder tree walk: The root node gets visited first, followed by left and right subtrees.
*Postorder tree walk: Nodes from the left subtree get visited first, followed by the right subtree, and finally, the root.
Following is a recursive implementation of the tree walks.
Balanced binary search trees
Without rebalancing, insertions or deletions in a binary search tree may lead to degeneration, resulting in a height of the tree (where is number of items in a tree), so that the lookup performance is deteriorated to that of a linear search. Keeping the search tree balanced and height bounded by is a key to the usefulness of the binary search tree. This can be achieved by "self-balancing" mechanisms during the updation operations to the tree designed to maintain the tree height to the binary logarithmic complexity.Height-balanced trees
A tree is height-balanced if the heights of the left sub-tree and right sub-tree are guaranteed to be related by a constant factor. This property was introduced by theAVL tree
In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by m ...
and continued by the red–black tree. The heights of all the nodes on the path from the root to the modified leaf node have to be observed and possibly corrected on every insert and delete operation to the tree.
Weight-balanced trees
In a weight-balanced tree, the criterion of a balanced tree is the number of leaves of the subtrees. The weights of the left and right subtrees differ at most by . However, the difference is bound by a ratio of the weights, since a strong balance condition of cannot be maintained with rebalancing work during insert and delete operations. The -weight-balanced trees gives an entire family of balance conditions, where each left and right subtrees have each at least a fraction of of the total weight of the subtree.Types
There are several self-balanced binary search trees, including T-tree,treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of i ...
, red-black tree, B-tree
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing fo ...
, 2–3 tree, and Splay tree
A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like self-balancing binary search trees, a splay tree performs basic operations such as insertion, look-up and removal ...
.
Examples of applications
Sort
Binary search trees are used in sorting algorithms such as tree sort, where all the elements are inserted at once and the tree is traversed at an in-order fashion. BSTs are also used inquicksort
Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than ...
.
Priority queue operations
Binary search trees are used in implementingpriority queue
In computer science, a priority queue is an abstract data type similar to a regular queue (abstract data type), queue or stack (abstract data type), stack abstract data type.
In a priority queue, each element has an associated ''priority'', which ...
s, using the node's key as priorities. Adding new elements to the queue follows the regular BST insertion operation but the removal operation depends on the type of priority queue:
* If it is an ascending order priority queue, removal of an element with the lowest priority is done through leftward traversal of the BST.
* If it is a descending order priority queue, removal of an element with the highest priority is done through rightward traversal of the BST.
See also
*Search tree
In computer science, a search tree is a tree data structure used for locating specific keys from within a set. In order for a tree to function as a search tree, the key for each node must be greater than any keys in subtrees on the left, and les ...
* Join-based tree algorithms
* Optimal binary search tree
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or Expected value, expected search time) for a given sequen ...
* Geometry of binary search trees
* Ternary search tree
In computer science, a ternary search tree is a type of trie (sometimes called a ''prefix tree'') where nodes are arranged in a manner similar to a binary search tree, but with up to three children rather than the binary tree's limit of two. Li ...
References
Further reading
* * * * * *External links
* Ben Pfaff''An Introduction to Binary Search Trees and Balanced Trees''.
(PDF; 1675 kB) 2004.
Binary Tree Visualizer
(JavaScript animation of various BT-based data structures) {{DEFAULTSORT:Binary search tree Articles with example C++ code Articles with example Python (programming language) code Binary trees Search trees