Banked curve on:
[Wikipedia]
[Google]
[Amazon]
A banked turn (or banking turn) is a turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn. For a road or railroad this is usually due to the roadbed having a transverse down-slope towards the inside of the curve. The bank angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the horizontal.
 As opposed to a vehicle riding along a flat circle, inclined edges add an additional force that keeps the vehicle in its path and prevents a car from being "dragged into" or "pushed out of" the circle (or a railroad wheel from moving sideways so as to nearly rub on the wheel
As opposed to a vehicle riding along a flat circle, inclined edges add an additional force that keeps the vehicle in its path and prevents a car from being "dragged into" or "pushed out of" the circle (or a railroad wheel from moving sideways so as to nearly rub on the wheel
 When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore, we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the direction of the center of the turn (the centripetal force):
:
Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and the vertical component of friction pointing downwards:
:
By solving the above equation for mass and substituting this value into our previous equation we get:
:
Solving for we get:
:
Where is the critical angle, such that . This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:
:
Notice
:
The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently, opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.
Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%. Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road
When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore, we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the direction of the center of the turn (the centripetal force):
:
Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and the vertical component of friction pointing downwards:
:
By solving the above equation for mass and substituting this value into our previous equation we get:
:
Solving for we get:
:
Where is the critical angle, such that . This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:
:
Notice
:
The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently, opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.
Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%. Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road
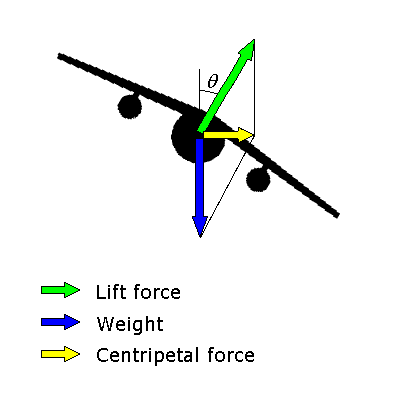 Because centripetal acceleration is:
:
During a balanced turn where the angle of bank is the lift acts at an angle away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component.
Newton's second law in the horizontal direction can be expressed mathematically as:
:
where:
: is the lift acting on the aircraft
: is the angle of bank of the aircraft
: is the
Because centripetal acceleration is:
:
During a balanced turn where the angle of bank is the lift acts at an angle away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component.
Newton's second law in the horizontal direction can be expressed mathematically as:
:
where:
: is the lift acting on the aircraft
: is the angle of bank of the aircraft
: is the
WMACi2017 W40-200m (51825456617).png, Sprinters leaning into a turn on a banked indoor track
Health and Safety Issues
the EU Roadex III project on health and safety issues raised by poorly maintained road networks. ;Aeronautics * Kermode, A.C. (1972) ''Mechanics of Flight'', Chapter 8, 10th Edition, Longman Group Limited, London * Clancy, L.J. (1975), ''Aerodynamics'', Pitman Publishing Limited, London {{ISBN, 0-273-01120-0 * Hurt, H.H. Jr, (1960), ''Aerodynamics for Naval Aviators'', A National Flightshop Reprint, Florida
aerospaceweb.org: Bank Angle and G's (math)
Pilot’s Handbook of Aeronautical Knowledge
Aerodynamics Aerial maneuvers Mechanics Transportation engineering https://edu-physics.com/2021/05/08/how-banking-of-road-will-help-the-vehicle-to-travel-along-a-circular-path-2/
Turn on flat surfaces
If the bank angle is zero, the surface is flat and thenormal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
is vertically upward. The only force keeping the vehicle turning on its path is friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
, or traction. This must be large enough to provide the centripetal force
Centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is the force that makes a body follow a curved trajectory, path. The direction of the centripetal force is always orthogonality, orthogonal to the motion of the bod ...
, a relationship that can be expressed as an inequality, assuming the car is driving in a circle of radius :
:
The expression on the right hand side is the centripetal acceleration multiplied by mass, the force required to turn the vehicle. The left hand side is the maximum frictional force, which equals the coefficient of friction multiplied by the normal force. Rearranging the maximum cornering speed is
:
Note that can be the coefficient for static or dynamic friction. In the latter case, where the vehicle is skidding around a bend, the friction is at its limit and the inequalities becomes equations. This also ignores effects such as downforce, which can increase the normal force and cornering speed.
Frictionless banked turn
flange
A flange is a protruded ridge, lip or rim (wheel), rim, either external or internal, that serves to increase shear strength, strength (as the flange of a steel beam (structure), beam such as an I-beam or a T-beam); for easy attachment/transfer o ...
). This force is the horizontal component of the vehicle's normal force (N). In the absence of friction, the normal force is the only one acting on the vehicle in the direction of the center of the circle. Therefore, as per Newton's second law, we can set the horizontal component of the normal force equal to mass multiplied by centripetal acceleration:Serway, p. 143
:
Because there is no motion in the vertical direction, the sum of all vertical forces acting on the system must be zero. Therefore, we can set the vertical component of the vehicle's normal force equal to its weight:
:
Solving the above equation for the normal force and substituting this value into our previous equation, we get:
:
This is equivalent to:
:
Solving for velocity we have:
:
This provides the velocity that in the absence of friction and with a given angle of incline and radius of curvature, will ensure that the vehicle will remain in its designated path. The magnitude of this velocity is also known as the "rated speed" (or "balancing speed" for railroads) of a turn or curve. Notice that the rated speed of the curve is the same for all massive objects, and a curve that is not inclined will have a rated speed of 0.
Banked turn with friction
 When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore, we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the direction of the center of the turn (the centripetal force):
:
Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and the vertical component of friction pointing downwards:
:
By solving the above equation for mass and substituting this value into our previous equation we get:
:
Solving for we get:
:
Where is the critical angle, such that . This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:
:
Notice
:
The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently, opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.
Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%. Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road
When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore, we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the direction of the center of the turn (the centripetal force):
:
Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and the vertical component of friction pointing downwards:
:
By solving the above equation for mass and substituting this value into our previous equation we get:
:
Solving for we get:
:
Where is the critical angle, such that . This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:
:
Notice
:
The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently, opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.
Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%. Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
and cross slope (angle of incline). A practical demonstration of how to evaluate improperly banked turns was developed in the EU Roadex III project. See the linked referenced document below.
Banked turn in aeronautics
When afixed-wing aircraft
A fixed-wing aircraft is a heavier-than-air aircraft, such as an airplane, which is capable of flight using aerodynamic lift. Fixed-wing aircraft are distinct from rotary-wing aircraft (in which a rotor mounted on a spinning shaft generate ...
is making a turn (changing its direction) the aircraft must roll to a banked position so that its wing
A wing is a type of fin that produces both Lift (force), lift and drag while moving through air. Wings are defined by two shape characteristics, an airfoil section and a planform (aeronautics), planform. Wing efficiency is expressed as lift-to-d ...
s are angled towards the desired direction of the turn. When the turn has been completed the aircraft must roll back to the wings-level position in order to resume straight flight.
When any moving vehicle is making a turn, it is necessary for the forces acting on the vehicle to add up to a net inward force, to cause centripetal acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are vector quantities (in that they have magn ...
. In the case of an aircraft making a turn, the force causing centripetal acceleration is the horizontal component of the lift acting on the aircraft.
In straight, level flight, the lift acting on the aircraft acts vertically upwards to counteract the weight of the aircraft which acts downwards. If the aircraft is to continue in level flight (i.e. at constant altitude
Altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum (geodesy), datum and a point or object. The exact definition and reference datum varies according to the context (e.g., aviation, geometr ...
), the vertical component must continue to equal the weight of the aircraft and so the pilot must pull back on the stick to apply the elevators
An elevator (American English) or lift (English in the Commonwealth of Nations, Commonwealth English) is a machine that vertically transports people or freight between levels. They are typically powered by electric motors that drive tracti ...
to pitch the nose up, and therefore increase the angle of attack
In fluid dynamics, angle of attack (AOA, α, or \alpha) is the angle between a Airfoil#Airfoil terminology, reference line on a body (often the chord (aircraft), chord line of an airfoil) and the vector (geometry), vector representing the relat ...
, generating an increase in the lift of the wing. The total (now angled) lift is greater than the weight of the aircraft, The excess lift is the horizontal component of the total lift, which is the net force
In mechanics, the net force is the sum of all the forces acting on an object. For example, if two forces are acting upon an object in opposite directions, and one force is greater than the other, the forces can be replaced with a single force tha ...
causing the aircraft to accelerate inward and execute the turn.
 Because centripetal acceleration is:
:
During a balanced turn where the angle of bank is the lift acts at an angle away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component.
Newton's second law in the horizontal direction can be expressed mathematically as:
:
where:
: is the lift acting on the aircraft
: is the angle of bank of the aircraft
: is the
Because centripetal acceleration is:
:
During a balanced turn where the angle of bank is the lift acts at an angle away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component.
Newton's second law in the horizontal direction can be expressed mathematically as:
:
where:
: is the lift acting on the aircraft
: is the angle of bank of the aircraft
: is the mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
of the aircraft
: is the true airspeed of the aircraft
: is the radius of the turn
In straight level flight, lift is equal to the aircraft weight. In turning flight the lift exceeds the aircraft weight, and is equal to the weight of the aircraft () divided by the cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
of the angle of bank:
:
where is the gravitational field strength.
The radius of the turn can now be calculated:
:
This formula shows that the radius of turn is proportional to the square of the aircraft's true airspeed. With a higher airspeed the radius of turn is larger, and with a lower airspeed the radius is smaller.
This formula also shows that the radius of turn decreases with the angle of bank. With a higher angle of bank the radius of turn is smaller, and with a lower angle of bank the radius is greater.
In a banked turn at constant altitude, the '' load factor'' is equal to . We can see that the load factor in straight and level flight is , since , and to generate sufficient lift to maintain constant altitude, the load factor must approach infinity as the bank angle approaches and approaches . This is physically impossible, because structural limitations of the aircraft or physical endurance of the occupants will be exceeded well before then.
Banked turn in athletics
Mostindoor track and field
Track and field (or athletics in British English) is a sport that includes Competition#Sports, athletic contests based on running, jumping, and throwing skills. The name used in North America is derived from where the sport takes place, a ru ...
venues have banked turns since the tracks are smaller than outdoor tracks. The tight turns on these small tracks are usually banked to allow athletes to lean inward and neutralize the centrifugal force
Centrifugal force is a fictitious force in Newtonian mechanics (also called an "inertial" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It appears to be directed radially away from the axi ...
as they race around the curve; the lean is especially noticeable on sprint events.
See also
* Camber angle * Cant (road/rail) * Coriolis force (perception) *Centripetal force
Centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is the force that makes a body follow a curved trajectory, path. The direction of the centripetal force is always orthogonality, orthogonal to the motion of the bod ...
* g-force
The g-force or gravitational force equivalent is a Specific force, mass-specific force (force per unit mass), expressed in Unit of measurement, units of standard gravity (symbol ''g'' or ''g''0, not to be confused with "g", the symbol for ...
* Oval track racing
Oval track racing is a form of motorsport that is contested on an oval-shaped race track. An oval track differs from a road course in that the layout resembles an oval with turns in only one direction, and the direction of traffic is almost u ...
References
Further reading
;Surface vehicles * Serway, Raymond. ''Physics for Scientists and Engineers.'' Cengage Learning, 2010.Health and Safety Issues
the EU Roadex III project on health and safety issues raised by poorly maintained road networks. ;Aeronautics * Kermode, A.C. (1972) ''Mechanics of Flight'', Chapter 8, 10th Edition, Longman Group Limited, London * Clancy, L.J. (1975), ''Aerodynamics'', Pitman Publishing Limited, London {{ISBN, 0-273-01120-0 * Hurt, H.H. Jr, (1960), ''Aerodynamics for Naval Aviators'', A National Flightshop Reprint, Florida
External links
;Surface vehicles * http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/carbank.gif * https://web.archive.org/web/20051222173550/http://whitts.alioth.net/ * http://www.batesville.k12.in.us/physics/PHYNET/Mechanics/Circular%20Motion/banked_no_friction.htm ;Aeronauticsaerospaceweb.org: Bank Angle and G's (math)
Pilot’s Handbook of Aeronautical Knowledge
Aerodynamics Aerial maneuvers Mechanics Transportation engineering https://edu-physics.com/2021/05/08/how-banking-of-road-will-help-the-vehicle-to-travel-along-a-circular-path-2/