Adomian decomposition method on:
[Wikipedia]
[Google]
[Amazon]
The Adomian decomposition method (ADM) is a semi-analytical method for solving ordinary and
/ref>
/ref> OI: 10.1108/03684920310463939
/ref> to obtain the boundary functions ''g''1*, ''g''2* that are compatible with any lateral set of conditions imposed. This makes it possible to find the analytical solution of any PDE boundary problem on a closed rectangle with the required accuracy, so allowing to solve a wide range of problems that the standard Adomian's method was not able to address. The first one perturbs the two boundary functions imposed at ''x'' = 0 and ''x'' = ''x''1 (condition 1-a) with a ''N''th-order polynomial in ''y'': ''p''1, ''p''2 in such a way that: ''f''1' = ''f''1 + ''p''1, ''f''2' = ''f''2 + ''p''2, where the norm of the two perturbation functions are smaller than the accuracy needed at the boundaries. These ''p''1, ''p''2 depend on a set of polynomial coefficients ''c''''i'', ''i'' = 1, ..., ''N''. Then, the Adomian method is applied and functions are obtained at the four boundaries which depend on the set of ''c''''i'', ''i'' = 1, ..., ''N''. Finally, a boundary function ''F''(''c''1, ''c''2, ..., ''c''''N'') is defined as the sum of these four functions, and the distance between ''F''(''c''1, ''c''2, ..., ''c''''N'') and the real boundary functions ((1-a) and (1-b)) is minimized. The problem has been reduced, in this way, to the global minimization of the function ''F''(''c''1, ''c''2, ..., ''c''''N'') which has a global minimum for some combination of the parameters ''c''''i'', ''i'' = 1, ..., ''N''. This minimum may be found by means of a genetic algorithm or by using some other optimization method, as the one proposed by Cherruault (1999). A second method to obtain analytic approximants of initial-boundary problems is to combine Adomian decomposition with spectral methods. Finally, the third method proposed by García-Olivares is based on imposing analytic solutions at the four boundaries, but modifying the original differential operator in such a way that it is different from the original one only in a narrow region close to the boundaries, and it forces the solution to satisfy exactly analytic conditions at the four boundaries.
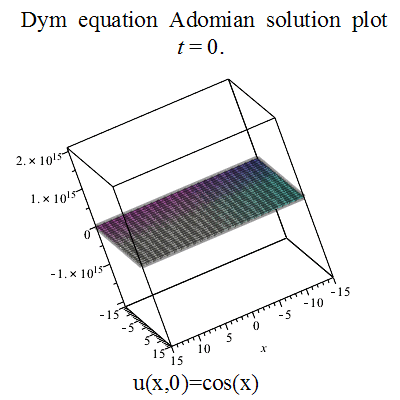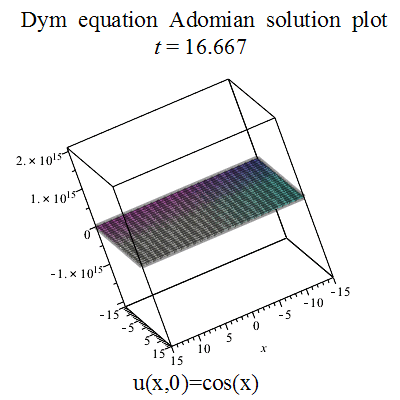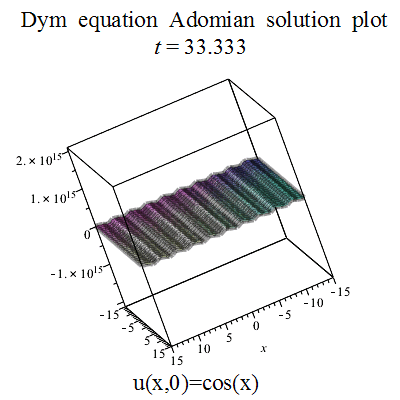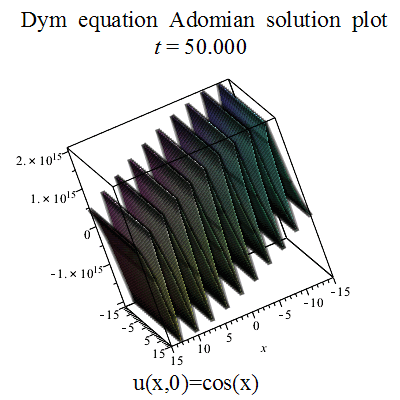

partial
Partial may refer to:
Mathematics
*Partial derivative, derivative with respect to one of several variables of a function, with the other variables held constant
** ∂, a symbol that can denote a partial derivative, sometimes pronounced "partial d ...
nonlinear differential equation
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathem ...
s. The method was developed from the 1970s to the 1990s by George Adomian, chair of the Center for Applied Mathematics at the University of Georgia
The University of Georgia (UGA or Georgia) is a Public university, public Land-grant university, land-grant research university with its main campus in Athens, Georgia, United States. Chartered in 1785, it is the oldest public university in th ...
.
It is further extensible to stochastic system
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a Indexed family, family of random variables in a probability space, where the Index set, index of the family often has the i ...
s by using the Ito integral.
The aim of this method is towards a unified theory for the solution of partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s (PDE); an aim which has been superseded by the more general theory of the homotopy analysis method.
The crucial aspect of the method is employment of the "Adomian polynomials" which allow for solution convergence of the nonlinear portion of the equation, without simply linearizing the system. These polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ...
s mathematically generalize to a Maclaurin series
Maclaurin or MacLaurin is a surname. Notable people with the surname include:
* Colin Maclaurin (1698–1746), Scottish mathematician
* Normand MacLaurin (1835–1914), Australian politician and university administrator
* Henry Normand MacLaurin ...
about an arbitrary external parameter; which gives the solution method more flexibility than direct Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion.
Ordinary differential equations
Adomian method is well suited to solve Cauchy problems, an important class of problems which include initial conditions problems.Application to a first order nonlinear system
An example of initial condition problem for an ordinary differential equation is the following: : : To solve the problem, the highest degree differential operator (written here as ''L'') is put on the left side, in the following way: : with ''L'' = d/d''t'' and . Now the solution is assumed to be an infinite series of contributions: : Replacing in the previous expression, we obtain: : Now we identify ''y''0 with some explicit expression on the right, and ''y''''i'', ''i'' = 1, 2, 3, ..., with some expression on the right containing terms of lower order than ''i''. For instance: : In this way, any contribution can be explicitly calculated at any order. If we settle for the four first terms, the approximant is the following: :Application to Blasius equation
A second example, with more complex boundary conditions is the Blasius equation for a flow in aboundary layer
In physics and fluid mechanics, a boundary layer is the thin layer of fluid in the immediate vicinity of a Boundary (thermodynamic), bounding surface formed by the fluid flowing along the surface. The fluid's interaction with the wall induces ...
:
:
With the following conditions at the boundaries:
:
Linear and non-linear operators are now called and , respectively. Then, the expression becomes:
:
and the solution may be expressed, in this case, in the following simple way:
:
where: If:
:
and:
:
Adomian’s polynomials to linearize the non-linear term can be obtained systematically by using the following rule:
:
where:
Boundary conditions must be applied, in general, at the end of each approximation. In this case, the integration constants must be grouped into three final independent constants. However, in our example, the three constants appear grouped from the beginning in the form shown in the formal solution above. After applying the two first boundary conditions we obtain the so-called Blasius series:
:
To obtain γ we have to apply boundary conditions at ∞, which may be done by writing the series as a Padé approximant
In mathematics, a Padé approximant is the "best" approximation of a function near a specific point by a rational function of given order. Under this technique, the approximant's power series agrees with the power series of the function it is ap ...
:
:
where ''L'' = ''M''. The limit at of this expression is ''a''''L''/''b''''M''.
If we choose ''b''0 = 1, ''M'' linear equations for the ''b'' coefficients are obtained:
:
Then, we obtain the ''a'' coefficients by means of the following sequence:
:
In our example:
:
Which when γ = 0.0408 becomes:
:
with the limit:
:
Which is approximately equal to 1 (from boundary condition (3)) with an accuracy of 4/1000.
Partial differential equations
Application to a rectangular system with nonlinearity
One of the most frequent problems in physical sciences is to obtain the solution of a (linear or nonlinear) partial differential equation which satisfies a set of functional values on a rectangular boundary. An example is the following problem: : with the following boundary conditions defined on a rectangle: : : This kind of partial differential equation appears frequently coupled with others inscience
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural sciences, which stu ...
and engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
. For instance, in the incompressible fluid
In fluid mechanics, or more generally continuum mechanics, incompressible flow is a flow in which the material density does not vary over time. Equivalently, the divergence of an incompressible flow velocity is zero. Under certain conditions, t ...
flow problem, the Navier–Stokes equations
The Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician Georg ...
must be solved in parallel with a Poisson equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with th ...
for the pressure.
Decomposition of the system
Let us use the following notation for the problem (1): : where ''L''x, ''L''y are double derivate operators and ''N'' is a non-linear operator. The formal solution of (2) is: : Expanding now u as a set of contributions to the solution we have: : By substitution in (3) and making a one-to-one correspondence between the contributions on the left side and the terms on the right side we obtain the following iterative scheme: : where the couple is the solution of the following system of equations: : here is the ''n''th-order approximant to the solution and ''N u'' has been consistently expanded in Adomian polynomials: : where and ''f''(''u'') = ''u''2 in the example (1). Here ''C''(ν, ''n'') are products (or sum of products) of ν components of ''u'' whose subscripts sum up to ''n'', divided by the factorial of the number of repeated subscripts. It is only a thumb-rule to order systematically the decomposition to be sure that all the combinations appearing are utilized sooner or later. The is equal to the sum of a generalized Taylor series about ''u''0. For the example (1) the Adomian polynomials are: : Other possible choices are also possible for the expression of ''A''''n''.Series solutions
Cherruault established that the series terms obtained by Adomian's method approach zero as 1/(''mn'')! if ''m'' is the order of the highest linear differential operator and that . With this method the solution can be found by systematically integrating along any of the two directions: in the ''x''-direction we would use expression (3); in the alternative ''y''-direction we would use the following expression: : where: ''c''(''x''), ''d''(''x'') is obtained from the boundary conditions at ''y'' = - ''y''''l'' and ''y'' = ''y''''l'': : If we call the two respective solutions ''x-partial solution'' and ''y-partial solution'', one of the most interesting consequences of the method is that the ''x-partial solution'' uses only the two boundary conditions (1-a) and the ''y-partial solution'' uses only the conditions (1-b). Thus, one of the two sets of boundary functions or is redundant, and this implies that a partial differential equation with boundary conditions on a rectangle cannot have arbitrary boundary conditions on the borders, since the conditions at ''x'' = ''x''1, ''x'' = ''x''2 must be consistent with those imposed at ''y'' = ''y''1 and ''y'' = ''y''2. An example to clarify this point is the solution of the Poisson problem with the following boundary conditions: : By using Adomian's method and a symbolic processor (such asMathematica
Wolfram (previously known as Mathematica and Wolfram Mathematica) is a software system with built-in libraries for several areas of technical computing that allows machine learning, statistics, symbolic computation, data manipulation, network ...
or Maple
''Acer'' is a genus of trees and shrubs commonly known as maples. The genus is placed in the soapberry family Sapindaceae.Stevens, P. F. (2001 onwards). Angiosperm Phylogeny Website. Version 9, June 2008 nd more or less continuously updated si ...
) it is easy to obtain the third order approximant to the solution. This approximant has an error lower than 5×10−16 in any point, as it can be proved by substitution in the initial problem and by displaying the absolute value of the residual obtained as a function of (''x'', ''y'').
The solution at ''y'' = -0.25 and ''y'' = 0.25 is given by specific functions that in this case are:
:
and ''g''2(''x'') = ''g''1(''x'') respectively.
If a (double) integration is now performed in the ''y''-direction using these two boundary functions the same solution will be obtained, which satisfy ''u''(''x''=0, ''y'') = 0 and ''u''(''x''=0.5, ''y'') = 0 and cannot satisfy any other condition on these borders.
Some people are surprised by these results; it seems strange that not all initial-boundary conditions must be explicitly used to solve a differential system. However, it is a well established fact that any elliptic equation has one and only one solution for any functional conditions in the four sides of a rectangle provided there is no discontinuity on the edges.
The cause of the misconception is that scientists and engineers normally think in a boundary condition in terms of weak convergence in a Hilbert space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The ...
(the distance to the boundary function is small enough to practical purposes). In contrast, Cauchy problems impose a point-to-point convergence to a given boundary function and to all its derivatives (and this is a quite strong condition!).
For the first ones, a function satisfies a boundary condition when the area (or another functional distance) between it and the true function imposed in the boundary is so small as desired; for the second ones, however, the function must tend to the true function imposed in any and every point of the interval.
The commented Poisson problem does not have a solution for any functional boundary conditions ''f''1, ''f''2, ''g''1, ''g''2; however, given ''f''1, ''f''2 it is always possible to find boundary functions ''g''1*, ''g''2* so close to ''g''1, ''g''2 as desired (in the weak convergence meaning) for which the problem has solution. This property makes it possible to solve Poisson's and many other problems with arbitrary boundary conditions but never for analytic functions exactly specified on the boundaries.
The reader can convince himself (herself) of the high sensitivity of PDE solutions to small changes in the boundary conditions by solving this problem integrating along the ''x''-direction, with boundary functions slightly different even though visually not distinguishable. For instance, the solution with the boundary conditions:
:
at ''x'' = 0 and ''x'' = 0.5, and the solution with the boundary conditions:
:
at ''x'' = 0 and ''x'' = 0.5, produce lateral functions with different sign convexity even though both functions are visually not distinguishable.
Solutions of elliptic problems and other partial differential equations are highly sensitive to small changes in the boundary function imposed when only two sides are used. And this sensitivity is not easily compatible with models that are supposed to represent real systems, which are described by means of measurements containing experimental errors and are normally expressed as initial-boundary value problems in a Hilbert space.
Improvements to the decomposition method
At least three methods have been reported/ref>
/ref> OI: 10.1108/03684920310463939
/ref> to obtain the boundary functions ''g''1*, ''g''2* that are compatible with any lateral set of conditions imposed. This makes it possible to find the analytical solution of any PDE boundary problem on a closed rectangle with the required accuracy, so allowing to solve a wide range of problems that the standard Adomian's method was not able to address. The first one perturbs the two boundary functions imposed at ''x'' = 0 and ''x'' = ''x''1 (condition 1-a) with a ''N''th-order polynomial in ''y'': ''p''1, ''p''2 in such a way that: ''f''1' = ''f''1 + ''p''1, ''f''2' = ''f''2 + ''p''2, where the norm of the two perturbation functions are smaller than the accuracy needed at the boundaries. These ''p''1, ''p''2 depend on a set of polynomial coefficients ''c''''i'', ''i'' = 1, ..., ''N''. Then, the Adomian method is applied and functions are obtained at the four boundaries which depend on the set of ''c''''i'', ''i'' = 1, ..., ''N''. Finally, a boundary function ''F''(''c''1, ''c''2, ..., ''c''''N'') is defined as the sum of these four functions, and the distance between ''F''(''c''1, ''c''2, ..., ''c''''N'') and the real boundary functions ((1-a) and (1-b)) is minimized. The problem has been reduced, in this way, to the global minimization of the function ''F''(''c''1, ''c''2, ..., ''c''''N'') which has a global minimum for some combination of the parameters ''c''''i'', ''i'' = 1, ..., ''N''. This minimum may be found by means of a genetic algorithm or by using some other optimization method, as the one proposed by Cherruault (1999). A second method to obtain analytic approximants of initial-boundary problems is to combine Adomian decomposition with spectral methods. Finally, the third method proposed by García-Olivares is based on imposing analytic solutions at the four boundaries, but modifying the original differential operator in such a way that it is different from the original one only in a narrow region close to the boundaries, and it forces the solution to satisfy exactly analytic conditions at the four boundaries.
Integral Equations
The Adomian decomposition method may also be applied to linear and nonlinearintegral equation
In mathematical analysis, integral equations are equations in which an unknown function appears under an integral sign. In mathematical notation, integral equations may thus be expressed as being of the form: f(x_1,x_2,x_3,\ldots,x_n ; u(x_1,x_2 ...
s to obtain solutions. This corresponds to the fact that many differential equation can be converted into integral equations.
Adomian Decomposition Method
The Adomian decomposition method for nonhomogenousFredholm integral equation
In mathematics, the Fredholm integral equation is an integral equation whose solution gives rise to Fredholm theory, the study of Fredholm kernels and Fredholm operators. The integral equation was studied by Ivar Fredholm. A useful method to ...
of the second kind goes as follows:
Given an integral equation of the form:
:
We assume we may express the solution in series form:
:
Plugging the series form into the integral equation then yields:
:
Assuming that the sum converges absolutely to we may integerchange the sum and integral as follows:
:
:
Expanding the sum on both sides yields:
:
Hence we may associate each in the following recurrent manner:
:
:
which gives us the solution in the solution form above.
Example
Given the Fredholm integral equation: : Since , we can set: : : : :... Hence the solution may be written as: : Since this is a telescoping series, we can see that every terms after cancels and may be regarded as "noise", Thus, becomes: :Gallery



See also
* Order of approximationReferences