|
Padé Approximant
In mathematics, a Padé approximant is the "best" approximation of a function near a specific point by a rational function of given order. Under this technique, the approximant's power series agrees with the power series of the function it is approximating. The technique was developed around 1890 by Henri Padé, but goes back to Georg Frobenius, who introduced the idea and investigated the features of rational approximations of power series. The Padé approximant often gives better approximation of the function than truncating its Taylor series, and it may still work where the Taylor series does not converge. For these reasons Padé approximants are used extensively in computer calculations. They have also been used as auxiliary functions in Diophantine approximation and transcendental number theory, though for sharp results ad hoc methods— in some sense inspired by the Padé theory— typically replace them. Since Padé approximant is a rational function, an artificial singul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Padé
Henri Eugène Padé (; 17 December 1863 – 9 July 1953) was a French mathematician, who is now remembered mainly for his development of Padé approximation techniques for functions using rational functions. Education and career Padé studied at École Normale Supérieure in Paris. He then spent a year at Leipzig University and University of Göttingen, where he studied under Felix Klein and Hermann Schwarz. In 1890 Padé returned to France, where he taught in Lille while preparing his doctorate under Charles Hermite. His doctoral thesis described what is now known as the Padé approximant. He then became an assistant professor at Université Lille Nord de France, where he succeeded Émile Borel as a professor of rational mechanics at École centrale de Lille. Padé taught at Lille until 1902, when he moved to Université de Poitiers The University of Poitiers (UP; french: Université de Poitiers) is a public university located in Poitiers, France. It is a member ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Euclidean Algorithm
In arithmetic and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common divisor (gcd) of integers ''a'' and ''b'', also the coefficients of Bézout's identity, which are integers ''x'' and ''y'' such that : ax + by = \gcd(a, b). This is a certifying algorithm, because the gcd is the only number that can simultaneously satisfy this equation and divide the inputs. It allows one to compute also, with almost no extra cost, the quotients of ''a'' and ''b'' by their greatest common divisor. also refers to a very similar algorithm for computing the polynomial greatest common divisor and the coefficients of Bézout's identity of two univariate polynomials. The extended Euclidean algorithm is particularly useful when ''a'' and ''b'' are coprime. With that provision, ''x'' is the modular multiplicative inverse of ''a'' modulo ''b'', and ''y'' is the modular multiplicative inverse of ''b'' modul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
North-Holland
North Holland ( nl, Noord-Holland, ) is a province of the Netherlands in the northwestern part of the country. It is located on the North Sea, north of South Holland and Utrecht, and west of Friesland and Flevoland. In November 2019, it had a population of 2,877,909 and a total area of , of which is water. From the 9th to the 16th century, the area was an integral part of the County of Holland. During this period West Friesland was incorporated. In the 17th and 18th century, the area was part of the province of Holland and commonly known as the Noorderkwartier (English: "Northern Quarter"). In 1840, the province of Holland was split into the two provinces of North Holland and South Holland. In 1855, the Haarlemmermeer was drained and turned into land. The provincial capital is Haarlem (pop. 161,265). The province's largest city and also the largest city in the Netherlands is the Dutch capital Amsterdam, with a population of 862,965 as of November 2019. The King's Commissione ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michela Redivo-Zaglia
Michela Redivo-Zaglia is an Italian numerical analyst known for her works on numerical linear algebra and on extrapolation-based acceleration of numerical methods. She is an associate professor in the department of mathematics at the University of Padua. Education and career Redivo-Zaglia earned a degree in mathematics at the University of Padua in 1975, and completed her Ph.D. in 1992 at the University of Lille in France. Her dissertation, ''Extrapolation, Méthodes de Lanczos et Polynômes Orthogonaux: Théorie et Conception de Logiciels'' was supervised by Claude Brezinski. She worked at the University of Padua, in the department of electronics and computer science, from 1984 to 1998, when she became an associate professor in 1998 at the University of Calabria The University of Calabria ( it, Università della Calabria, UNICAL) is a state-run university in Italy. Located in Arcavacata, a hamlet of Rende and a suburb of Cosenza, the university was founded in 1972. Among its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
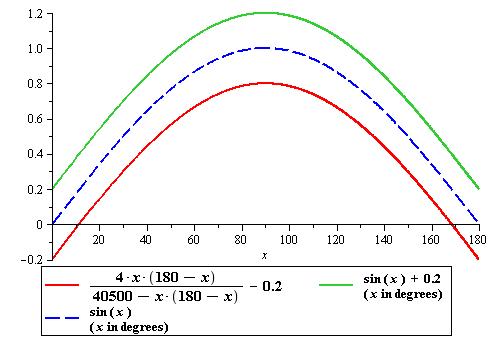
Bhaskara I's Sine Approximation Formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian mathematician. This formula is given in his treatise titled ''Mahabhaskariya''. It is not known how Bhaskara I arrived at his approximation formula. However, several historians of mathematics have put forward different hypotheses as to the method Bhaskara might have used to arrive at his formula. The formula is elegant, simple and enables one to compute reasonably accurate values of trigonometric sines without using any geometry whatsoever. The approximation formula The formula is given in verses 17 – 19, Chapter VII, Mahabhaskariya of Bhaskara I. A translation of the verses is given below: *(Now) I briefly state the rule (for finding the ''bhujaphala'' and the ''kotiphala'', etc.) without making use of the Rsine-differences 225, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Padé Table
In complex analysis, a Padé table is an array, possibly of infinite extent, of the rational Padé approximants :''R''''m'', ''n'' to a given complex formal power series. Certain sequences of approximants lying within a Padé table can often be shown to correspond with successive convergents of a continued fraction representation of a holomorphic or meromorphic function. History Although earlier mathematicians had obtained sporadic results involving sequences of rational approximations to transcendental functions, Frobenius (in 1881) was apparently the first to organize the approximants in the form of a table. Henri Padé further expanded this notion in his doctoral thesis ''Sur la representation approchee d'une fonction par des fractions rationelles'', in 1892. Over the ensuing 16 years Padé published 28 additional papers exploring the properties of his table, and relating the table to analytic continued fractions. Modern interest in Padé tables was revived by H. S. Wall a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The simultaneous parametric plot of and is the Euler spiral (also known as the Cornu spiral or clothoid). Definition 250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the following power series expansions that converge for all : \begin S(x) &= \int_0^x \sin\left(t^2\right)\,dt = \sum_^(-1)^n \frac, \\ C(x) &= \int_0^x \cos\left(t^2\right)\,dt = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel function is a generalizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobi Elliptic Functions
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum (see also pendulum (mathematics)), as well as in the design of electronic elliptic filters. While trigonometry, trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation \operatorname for \sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by . Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular, but his work was published much later. Overview There are twelve Jacob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeta Regularization
Zeta (, ; uppercase Ζ, lowercase ζ; grc, ζῆτα, el, ζήτα, label=Demotic Greek, classical or ''zē̂ta''; ''zíta'') is the sixth letter of the Greek alphabet. In the system of Greek numerals, it has a value of 7. It was derived from the Phoenician letter zayin . Letters that arose from zeta include the Roman Z and Cyrillic З. Name Unlike the other Greek letters, this letter did not take its name from the Phoenician letter from which it was derived; it was given a new name on the pattern of beta, eta and theta. The word ''zeta'' is the ancestor of ''zed'', the name of the Latin letter Z in Commonwealth English. Swedish and many Romanic languages (such as Italian and Spanish) do not distinguish between the Greek and Roman forms of the letter; "''zeta''" is used to refer to the Roman letter Z as well as the Greek letter. Uses Letter The letter ζ represents the voiced alveolar fricative in Modern Greek. The sound represented by zeta in Greek before 400&n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Jacobi Elliptic Functions")
