Algorithmics Of Sudoku on:
[Wikipedia]
[Google]
[Amazon]
 A standard
A standard
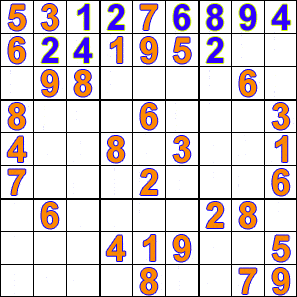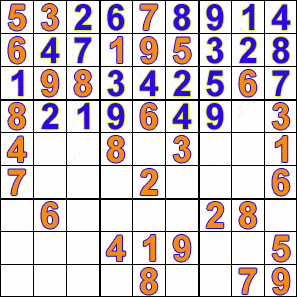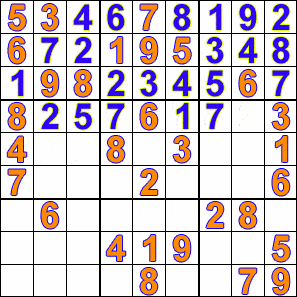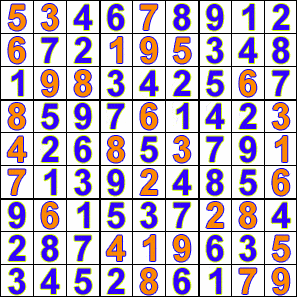 Some hobbyists have developed computer programs that will solve Sudoku puzzles using a
Some hobbyists have developed computer programs that will solve Sudoku puzzles using a
A Pencil-and-Paper Algorithm for Solving Sudoku Puzzles
Sudoku Abstract strategy games Search algorithms
Sudoku
Sudoku (; ; originally called Number Place) is a logic puzzle, logic-based, combinatorics, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and ...
contains 81 cells, in a 9×9 grid, and has 9 boxes, each box being the intersection of the first, middle, or last 3 rows, and the first, middle, or last 3 columns. Each cell may contain a number from one to nine, and each number can only occur once in each row, column, and box. A Sudoku starts with some cells containing numbers (''clues''), and the goal is to solve the remaining cells. Proper Sudokus have one solution. Players and investigators use a wide range of computer algorithms to solve Sudokus, study their properties, and make new puzzles, including Sudokus with interesting symmetries and other properties.
There are several computer algorithms that will solve 9×9 puzzles ( = 9) in fractions of a second, but combinatorial explosion
In mathematics, a combinatorial explosion is the rapid growth of the complexity of a problem due to the way its combinatorics depends on input, constraints and bounds. Combinatorial explosion is sometimes used to justify the intractability of cert ...
occurs as increases, creating limits to the properties of Sudokus that can be constructed, analyzed, and solved as increases.
Techniques
Backtracking
backtracking
Backtracking is a class of algorithms for finding solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons a candidate ("backtracks") as soon as it de ...
algorithm, which is a type of brute force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique and algorithmic paradigm that consists of systematically checking all possible candidates for whether or n ...
. Backtracking is a ''depth-first search
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible al ...
'' (in contrast to a ''breadth-first search
Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. It starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next dept ...
''), because it will completely explore one branch to a possible solution before moving to another branch. Although it has been established that approximately 5.96 x 1026 final grids exist, a brute force algorithm can be a practical method to solve Sudoku puzzles.
A brute force algorithm visits the empty cells in some order, filling in digits sequentially, or backtracking when the number is found to be not valid.
Briefly, a program would solve a puzzle by placing the digit "1" in the first cell and checking if it is allowed to be there. If there are no violations (checking row, column, and box constraints) then the algorithm advances to the next cell and places a "1" in that cell. When checking for violations, if it is discovered that the "1" is not allowed, the value is advanced to "2". If a cell is discovered where none of the 9 digits is allowed, then the algorithm leaves that cell blank and moves back to the previous cell. The value in that cell is then incremented by one. This is repeated until the allowed value in the last (81st) cell is discovered.
The animation shows how a Sudoku is solved with this method. The puzzle's clues (red numbers) remain fixed while the algorithm tests each unsolved cell with a possible solution. Notice that the algorithm may discard all the previously tested values if it finds the existing set does not fulfill the constraints of the Sudoku.
Advantages of this method are:
* A solution is guaranteed (as long as the puzzle is valid).
* Solving time is mostly unrelated to degree of difficulty
Degree of difficulty (DD, sometimes called tariff or grade) is a rating used in several sports and other competitions to indicate the technical difficulty of a skill, performance, or course, often as a factor in scoring. Sports which incorporate a ...
.
* The algorithm (and therefore the program code) is simpler than other algorithms, especially compared to strong algorithms that ensure a solution to the most difficult puzzles.
The disadvantage of this method is that the solving time may be slow compared to algorithms modeled after deductive methods. One programmer reported that such an algorithm may typically require as few as 15,000 cycles, or as many as 900,000 cycles to solve a Sudoku, each cycle being the change in position of a "pointer" as it moves through the cells of a Sudoku.
A different approach which also uses backtracking, draws from the fact that in the solution to a standard sudoku the distribution for every individual symbol (value) must be one of only 46656 patterns.
In manual sudoku solving this technique is referred to as pattern overlay or using templates and is confined to filling in the last values only.
A library with all the possible patterns may get loaded or created at program start. Then every given symbol gets assigned a filtered set with those patterns, which are in accordance with the given clues.
In the last step, the actual backtracking part, patterns from these sets are tried to be combined or overlayed in a non-conflicting way until the one permissible combination is hit upon.
The Implementation is exceptionally easy when using bit vectors, because for all the tests only bit-wise logical operations are needed, instead of any nested iterations across rows and columns.
Significant optimization can be achieved by reducing the sets of patterns even further during filtering. By testing every questionable pattern against all the reduced sets that were already accepted for the other symbols the total number of patterns left for backtracking is greatly diminished.
And as with all sudoku brute-force techniques, run time can be vastly reduced by first applying some of the most simple solving practices which may fill in some 'easy' values.
A Sudoku can be constructed to work against backtracking. Assuming the solver works from top to bottom (as in the animation), a puzzle with few clues (17), no clues in the top row, and has a solution "987654321" for the first row, would work in opposition to the algorithm. Thus the program would spend significant time "counting" upward before it arrives at the grid which satisfies the puzzle. In one case, a programmer found a brute force program required six hours to arrive at the solution for such a Sudoku (albeit using a 2008-era computer). Such a Sudoku can be solved nowadays in less than 1 second using an exhaustive search routine and faster processors.p:25
Stochastic search / optimization methods
Sudoku can be solved using stochastic (random-based) algorithms.Lewis, R (2007) ''Metaheuristics Can Solve Sudoku Puzzles'' Journal of Heuristics, vol. 13 (4), pp 387-401.Perez, Meir and Marwala, Tshilidzi (2008) ''Stochastic Optimization Approaches for Solving Sudoku'' arXiv:0805.0697. An example of this method is to: # Randomly assign numbers to the blank cells in the grid. # Calculate the number of errors. # "Shuffle" the inserted numbers until the number of mistakes is reduced to zero. A solution to the puzzle is then found. Approaches for shuffling the numbers includesimulated annealing
Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. ...
, genetic algorithm
In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to g ...
and tabu search Tabu search (TS) is a metaheuristic search method employing local search methods used for mathematical optimization. It was created by Fred W. Glover in 1986
and formalized in 1989.
Local (neighborhood) searches take a potential solution to a ...
. Stochastic-based algorithms are known to be fast, though perhaps not as fast as deductive techniques. Unlike the latter however, optimisation algorithms do not necessarily require problems to be logic-solvable, giving them the potential to solve a wider range of problems. Algorithms designed for graph colouring are also known to perform well with Sudokus.Lewis, R. ''A Guide to Graph Colouring: Algorithms and Applications''. Springer International Publishers, 2015. It is also possible to express a Sudoku as an integer linear programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective ...
problem. Such approaches get close to a solution quickly, and can then use branching towards the end. The simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming.
The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are ...
is able to solve proper Sudokus, indicating if the Sudoku is not valid (no solution). If there is more than one solution (non-proper Sudokus) the simplex algorithm will generally yield a solution with fractional amounts of more than one digit in some squares. However, for proper Sudokus, linear programming presolve techniques alone will deduce the solution without any need for simplex iterations. The logical rules used by presolve techniques for the reduction of LP problems include the set of logical rules used by humans to solve Sudokus.
Constraint programming
A Sudoku may also be modelled as aconstraint satisfaction problem
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite const ...
. In his paper ''Sudoku as a Constraint Problem'', Helmut Simonis describes many ''reasoning algorithms'' based on constraints which can be applied to model and solve problems. Some constraint solvers include a method to model and solve Sudokus, and a program may require fewer than 100 lines of code to solve a simple Sudoku. If the code employs a strong reasoning algorithm, incorporating backtracking is only needed for the most difficult Sudokus. An algorithm combining a constraint-model-based algorithm with backtracking would have the advantage of fast solving time – of the order of a few milliseconds – and the ability to solve all sudokus.
Exact cover
Sudoku puzzles may be described as anexact cover
In the mathematical field of combinatorics, given a collection \mathcal of subsets of a set X, an exact cover is a subcollection \mathcal^ of \mathcal such that each element in X is contained in ''exactly one'' subset in \mathcal^.
One says that e ...
problem, or more precisely, an exact hitting set problem. This allows for an elegant description of the problem and an efficient solution. Modelling Sudoku as an exact cover problem and using an algorithm such as Knuth's Algorithm X and his Dancing Links technique "is the method of choice for rapid finding easured in microsecondsof all possible solutions to Sudoku puzzles."
An alternative approach is the use of Gauss elimination in combination with column and row striking.
Relations and residuals
Let ''Q'' be the 9x9 Sudoku matrix, ''N'' = , and ''X'' represent a generic row, column, or block. ''N'' supplies symbols for filling ''Q'' as well as theindex set
In mathematics, an index set is a set whose members label (or index) members of another set. For instance, if the elements of a set may be ''indexed'' or ''labeled'' by means of the elements of a set , then is an index set. The indexing consists ...
for the 9 elements of any ''X''. The given elements ''q'' in ''Q'' represent a univalent relation from ''Q'' to ''N''. The solution ''R'' is a ''total relation'' and hence a function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-orie ...
. Sudoku rules require that the restriction of ''R'' to ''X'' is a bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
, so any partial solution ''C'', restricted to an ''X'', is a partial permutation
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set ''S''
is a bijection between two specified subsets of ''S''. That is, it is defined by two subsets ''U'' and ''V'' of equal size, and a one-to-one ...
of ''N''.
Let ''T'' = , so ''T'' has 27 elements. An ''arrangement'' is either a partial permutation or a permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
on ''N''. Let ''Z'' be the set of all arrangements on ''N''. A partial solution ''C'' can be reformulated to include the rules as a composition of relations
In the mathematics of binary relations, the composition of relations is the forming of a new binary relation from two given binary relations ''R'' and ''S''. In the calculus of relations, the composition of relations is called relative multiplica ...
''A'' (one-to-three) and ''B'' requiring compatible arrangements:
:
Solution of the puzzle, suggestions for new ''q'' to enter ''Q'', come from prohibited arrangements , the complement
Complement may refer to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-class collections into complementary sets
* Complementary color, in the visu ...
of ''C'' in ''Q''x''Z'': useful tools in the calculus of relations are residuals:
: maps ''T'' to ''Z'', and
: maps ''Q'' to ''T''.
See also
*Sudoku
Sudoku (; ; originally called Number Place) is a logic puzzle, logic-based, combinatorics, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and ...
* Mathematics of Sudoku
Mathematics can be used to study Sudoku puzzles to answer questions such as "How many filled Sudoku grids are there?", "What is the minimal number of clues in a valid puzzle?" and "In what ways can Sudoku grids be symmetric?" through the use o ...
* Combinatorial explosion
In mathematics, a combinatorial explosion is the rapid growth of the complexity of a problem due to the way its combinatorics depends on input, constraints and bounds. Combinatorial explosion is sometimes used to justify the intractability of cert ...
(with summary of grid count of Sudoku compared to Latin squares)
* Glossary of Sudoku
References
External links
* http://diuf.unifr.ch/pai/people/juillera/Sudoku/Sudoku.html ''Sudoku Explainer by Nicolas Juillerat'' (Popular for rating Sudokus in general) {{Archive url, url=https://web.archive.org/web/20131112230157/http://diuf.unifr.ch/pai/people/juillera/Sudoku/Sudoku.html, date=2013-11-12A Pencil-and-Paper Algorithm for Solving Sudoku Puzzles
Sudoku Abstract strategy games Search algorithms