Airmass

In astronomy, air mass or airmass is a measure of the amount of air along the line of sight when observing a star or other celestial source from below Earth's atmosphere ( Green 1992). It is formulated as the integral of air density along the light ray.

As it penetrates the atmosphere, light is attenuated by scattering and absorption; the thicker atmosphere through which it passes, the greater the attenuation. Consequently, celestial bodies when nearer the horizon appear less bright than when nearer the zenith. This attenuation, known as atmospheric extinction, is described quantitatively by the Beer–Lambert law.

"Air mass" normally indicates ''relative air mass'', the ratio of absolute air masses (as defined above) at oblique incidence relative to that at zenith. So, by definition, the relative air mass at the zenith is 1. Air mass increases as the angle between the source and the zenith increases, reaching a value of approximately 38 at the horizon. Air mass can be less than one at an elevation greater than sea level; however, most closed-form expressions for air mass do not include the effects of the observer's elevation, so adjustment must usually be accomplished by other means.

Tables of air mass have been published by numerous authors, including Bemporad (1904), Allen (1976), and Kasten and Young (1989).

Definition

The ''absolute air mass'' is defined as:

:$\sigma = \int \rho \, \mathrm d s \,.$

where $\rho$ is volumetric density of air. Thus $\sigma$ is a type of oblique column density.

In the vertical direction, the ''absolute air mass at zenith'' is:

:$\sigma_\mathrm = \int \rho \, \mathrm d z$

So $\sigma_\mathrm$ is a type of vertical column density.

Finally, the ''relative air mass'' is:

:$X = \frac \sigma$

Assuming air density is uniform allows removing it out of the integrals. The absolute air mass then simplifies to a product:

:$\sigma = \bar\rho s$

where $\bar\rho=\mathrm$ is the average density and the arc length $s$ of the oblique and zenith light paths are:

:$s = \int \, \mathrm d s$
:$s_\mathrm = \int \, \mathrm d z$

In the corresponding simplified relative air mass, the average density cancels out in the fraction, leading to the ratio of path lengths:

:$X = \frac s \,.$

Further simplifications are often made, assuming straight-line propagation (neglecting ray bending), as discussed below.

Calculation

Background

The angle of a celestial body with the zenith is the ''zenith angle'' (in astronomy, commonly referred to as the ''zenith distance''). A body's angular position can also be given in terms of ''altitude'', the angle above the geometric horizon; the altitude $h$ and the zenith angle $z$ are thus related by

:$h = 90^\circ - z \,.$

Atmospheric refraction causes light entering the atmosphere to follow an approximately circular path that is slightly longer than the geometric path. Air mass must take into account the longer path ( Young 1994). Additionally, refraction causes a celestial body to appear higher above the horizon than it actually is; at the horizon, the difference between the true zenith angle and the apparent zenith angle is approximately 34 minutes of arc. Most air mass formulas are based on the apparent zenith angle, but some are based on the true zenith angle, so it is important to ensure that the correct value is used, especially near the horizon.

Plane-parallel atmosphere

When the zenith angle is small to moderate, a good approximation is given by assuming a homogeneous plane-parallel atmosphere (i.e., one in which density is constant and Earth's curvature is ignored). The air mass $X$ then is simply the secant of the zenith angle $z$:

:$X = \sec\, z \,.$

At a zenith angle of 60°, the air mass is approximately 2. However, because the Earth is not flat, this formula is only usable for zenith angles up to about 60° to 75°, depending on accuracy requirements. At greater zenith angles, the accuracy degrades rapidly, with $X = \sec\, z$ becoming infinite at the horizon; the horizon air mass in the more-realistic spherical atmosphere is usually less than 40.

Interpolative formulas

Many formulas have been developed to fit tabular values of air mass; one by Young and Irvine (1967) included a simple corrective term:

:X = \sec\,z_\mathrm t \, \left 1 - 0.0012 \,(\sec^2 z_\mathrm t - 1) \right \,,

where $z_\mathrm t$ is the true zenith angle. This gives usable results up to approximately 80°, but the accuracy degrades rapidly at greater zenith angles. The calculated air mass reaches a maximum of 11.13 at 86.6°, becomes zero at 88°, and approaches negative infinity at the horizon. The plot of this formula on the accompanying graph includes a correction for atmospheric refraction so that the calculated air mass is for apparent rather than true zenith angle.

Hardie (1962) introduced a polynomial in $\sec\,z - 1$:

:$X = \sec\,z \,-\, 0.0018167 \,(\sec\,z \,-\, 1) \,-\, 0.002875 \,(\sec\,z \,-\, 1)^2 \,-\, 0.0008083 \,(\sec\,z \,-\, 1)^3 \,$

which gives usable results for zenith angles of up to perhaps 85°. As with the previous formula, the calculated air mass reaches a maximum, and then approaches negative infinity at the horizon.

Rozenberg (1966) suggested

:$X = \left (\cos\,z + 0.025 e^ \right )^ \,,$

which gives reasonable results for high zenith angles, with a horizon air mass of 40.

Kasten and Young (1989) developed

:$X = \frac \,,$

which gives reasonable results for zenith angles of up to 90°, with an air mass of approximately 38 at the horizon. Here the second $z$ term is in ''degrees''.

Young (1994) developed

:$X = \frac \,$

in terms of the true zenith angle $z_\mathrm t$, for which he claimed a maximum error (at the horizon) of 0.0037 air mass.

Pickering (2002) developed
:$X = \frac \,,$

where $h$ is apparent altitude $(90^\circ - z)$ in degrees. Pickering claimed his equation to have a tenth the error of Schaefer (1998) near the horizon.

Atmospheric models

Interpolative formulas attempt to provide a good fit to tabular values of air mass using minimal computational overhead. The tabular values, however, must be determined from measurements or atmospheric models that derive from geometrical and physical considerations of Earth and its atmosphere.

Nonrefracting spherical atmosphere

If atmospheric refraction is ignored, it can be shown from simple geometrical considerations ( Schoenberg 1929, 173) that the path $s$ of a light ray at zenith angle
$z$ through a radially symmetrical atmosphere of height $y_$ above the Earth is given by

:$s = \sqrt - R_\mathrm \cos\, z \,$

or alternatively,

:$s = \sqrt - R_\mathrm \cos\, z \,$

where $R_\mathrm E$ is the radius of the Earth.

The relative air mass is then:

:$X = \frac s = \frac \sqrt - \frac \cos\, z \,.$

Homogeneous atmosphere

If the atmosphere is homogeneous (i.e., density is constant), the atmospheric height $y_$ follows from hydrostatic considerations as:

:$y_\mathrm = \frac \,,$

where $k$ is Boltzmann's constant, $T_0$ is the sea-level temperature, $m$ is the molecular mass of air, and $g$ is the acceleration due to gravity. Although this is the same as the pressure scale height of an isothermal atmosphere, the implication is slightly different. In an isothermal atmosphere, 37% (1/ e) of the atmosphere is above the pressure scale height; in a homogeneous atmosphere, there is no atmosphere above the atmospheric height.

Taking $T_0 = \mathrm$, $m = \mathrm$, and $g = \mathrm$ gives $y_\mathrm \approx \mathrm$. Using Earth's mean radius of 6371 km, the sea-level air mass at the horizon is

:$X_\mathrm = \sqrt \approx 38.87 \,.$

The homogeneous spherical model slightly underestimates the rate of increase in air mass near the horizon; a reasonable overall fit to values determined from more rigorous models can be had by setting the air mass to match a value at a zenith angle less than 90°. The air mass equation can be rearranged to give

:$\frac = \frac \,;$

matching Bemporad's value of 19.787 at $z$ = 88°
gives $R_\mathrm / y_\mathrm$ ≈ 631.01 and
$X_\mathrm$ ≈ 35.54. With the same value for $R_\mathrm$ as above, $y_\mathrm$ ≈ 10,096 m.

While a homogeneous atmosphere isn't a physically realistic model, the approximation is reasonable as long as the scale height of the atmosphere is small compared to the radius of the planet. The model is usable (i.e., it does not diverge or go to zero) at all zenith angles, including those greater than 90° (''see'' ). The model requires comparatively little computational overhead, and if high accuracy is not required, it gives reasonable results.
However, for zenith angles less than 90°, a better fit to accepted values of air mass can be had with several
of the interpolative formulas.

Variable-density atmosphere

In a real atmosphere, density is not constant (it decreases with elevation above mean sea level. The absolute air mass for the geometrical light path discussed above, becomes, for a sea-level observer,

:$\sigma = \int_0^ \frac \,.$

Isothermal atmosphere

Several basic models for density variation with elevation are commonly used. The simplest, an isothermal atmosphere, gives

:$\rho = \rho_0 e^ \,,$

where $\rho_0$ is the sea-level density and $H$ is the pressure scale height. When the limits of integration are zero and infinity, the result is known as Chapman function. An approximate result is obtained if some high-order terms are dropped, yielding ( Young 1974, 147),

:$X \approx \sqrt \exp \, \mathrm \left ( \sqrt \right ) \,.$

An approximate correction for refraction can be made by taking ( Young 1974, 147)

:$R = 7/6 \, R_\mathrm E \,,$

where $R_\mathrm E$ is the physical radius of the Earth. At the horizon, the approximate equation becomes

:$X_\mathrm \approx \sqrt \,.$

Using a scale height of 8435 m, Earth's mean radius of 6371 km, and including the correction for refraction,

:$X_\mathrm \approx 37.20 \,.$

Polytropic atmosphere

The assumption of constant temperature is simplistic; a more realistic model is the polytropic atmosphere, for which

:$T = T_0 - \alpha y \,,$

where $T_0$ is the sea-level temperature and $\alpha$ is the temperature lapse rate. The density as a function of elevation is

:$\rho = \rho_0 \left ( 1 - \frac \alpha T_0 y \right )^ \,,$

where $\kappa$ is the polytropic exponent (or polytropic index). The air mass integral for the polytropic model does not lend itself to a closed-form solution except at the zenith, so the integration usually is performed numerically.

Layered atmosphere

Earth's atmosphere consists of multiple layers with different temperature and density characteristics; common atmospheric models include the International Standard Atmosphere and the US Standard Atmosphere. A good approximation for many purposes is a polytropic troposphere of 11 km height with a lapse rate of 6.5 K/km and an isothermal stratosphere of infinite height ( Garfinkel 1967), which corresponds very closely to the first two layers of the International Standard Atmosphere. More layers can be used if greater accuracy is required.

Refracting radially symmetrical atmosphere

When atmospheric refraction is considered, ray tracing becomes necessary, and the absolute air mass integral becomes

:$\sigma = \int_^ \frac \,$

where $n_\mathrm$ is the index of refraction of air at the observer's elevation $y_\mathrm$ above sea level, $n$ is the index of refraction at elevation $y$ above sea level, $r_\mathrm = R_\mathrm + y_\mathrm$,
$r = R_\mathrm + y$ is the distance from the center of the Earth to a point at elevation $y$, and $r_\mathrm = R_\mathrm + y_\mathrm$ is distance to the upper limit of the atmosphere at elevation $y_\mathrm$. The index of refraction in terms of density is usually given to sufficient accuracy ( Garfinkel 1967) by the Gladstone–Dale relation

:$\frac = \frac \,.$

Rearrangement and substitution into the absolute air mass integral gives

:$\sigma = \int_^ \frac \,.$

The quantity $n_\mathrm - 1$ is quite small; expanding the first term in parentheses, rearranging several times, and ignoring terms in $(n_\mathrm - 1)^2$ after each rearrangement, gives ( Kasten and Young 1989)

:$\sigma = \int_^ \frac \,.$

Homogeneous spherical atmosphere with elevated observer

In the figure at right, an observer at O is at an elevation $y_\mathrm$ above sea level in a uniform radially symmetrical atmosphere of height $y_\mathrm$. The path length of a light ray at zenith angle $z$ is $s$; $R_\mathrm$ is the radius of the Earth. Applying the law of cosines to triangle OAC,

:$\begin \left(R_+y_\right)^ & =s^+\left(R_+y_\right)^-2\left(R_+y_\right)s \cos\left(180^-z\right)\\ & =s^+\left(R_+y_\right)^+2\left(R_+y_\right)s\cos z\end$

expanding the left- and right-hand sides, eliminating the common terms, and rearranging gives

:$+2\left( + \right)s\cos z-2-y_^+2+y_^=0 \,.$

Solving the quadratic for the path length ''s'', factoring, and rearranging,

:$s=\pm \sqrt-(+)\cos z \,.$

The negative sign of the radical gives a negative result, which is not physically meaningful. Using the positive sign, dividing by $y_\mathrm$, and cancelling common terms and rearranging gives the relative air mass:

:$X=\sqrt-\frac\cos z \,.$

With the substitutions $\hat = R_\mathrm / y_\mathrm$ and $\hat = y_\mathrm / y_\mathrm$, this can be given as

:$X=\sqrt \; - \; (\hat+\hat)\cos z \,.$

When the observer's elevation is zero, the air mass equation simplifies to

:$X=\sqrt-\frac\cos z \,.$

In the limit of grazing incidence, the absolute airmass equals the distance to the horizon. Furthermore, if the observer is elevated, the horizon zenith angle can be greater than 90°.

Nonuniform distribution of attenuating species

Atmospheric models that derive from hydrostatic considerations assume an atmosphere of constant composition and a single mechanism of extinction, which isn't quite correct. There are three main sources of attenuation ( Hayes and Latham 1975): Rayleigh scattering by air molecules, Mie scattering by aerosols, and molecular absorption (primarily by ozone). The relative contribution of each source varies with elevation above sea level, and the concentrations of aerosols and ozone cannot be derived simply from hydrostatic considerations.

Rigorously, when the extinction coefficient depends on elevation, it must be determined as part of the air mass integral, as described by Thomason, Herman, and Reagan (1983). A compromise approach often is possible, however. Methods for separately calculating the extinction from each species using closed-form expressions are described in Schaefer (1993) and Schaefer (1998). The latter reference includes source code for a BASIC program to perform the calculations. Reasonably accurate calculation of extinction can sometimes be done by using one of the simple air mass formulas and separately determining extinction coefficients for each of the attenuating species
( Green 1992, Pickering 2002).

Implications

Air mass and astronomy

In optical astronomy, the air mass provides an indication of the deterioration of the observed image, not only as regards direct effects of spectral absorption, scattering and reduced brightness, but also an aggregation of visual aberrations, e.g. resulting from atmospheric turbulence, collectively referred to as the quality of the " seeing". On bigger telescopes, such as the WHT ( Wynne and Warsick 1988) and VLT ( Avila, Rupprecht, and Becker 1997), the atmospheric dispersion can be so severe that it affects the pointing of the telescope to the target. In such cases an atmospheric dispersion compensator is used, which usually consists of two prisms.

The Greenwood frequency and Fried parameter, both relevant for adaptive optics, depend on the air mass above them (or more specifically, on the zenith angle).

In radio astronomy the air mass (which influences the optical path length) is not relevant. The lower layers of the atmosphere, modeled by the air mass, do not significantly impede radio waves, which are of much lower frequency than optical waves. Instead, some radio waves are affected by the ionosphere in the upper atmosphere. Newer aperture synthesis radio telescopes are especially affected by this as they “see” a much larger portion of the sky and thus the ionosphere. In fact, LOFAR needs to explicitly calibrate for these distorting effects ( van der Tol and van der Veen 2007; de Vos, Gunst, and Nijboer 2009), but on the other hand can also study the ionosphere by instead measuring these distortions ( Thidé 2007).

Air mass and solar energy

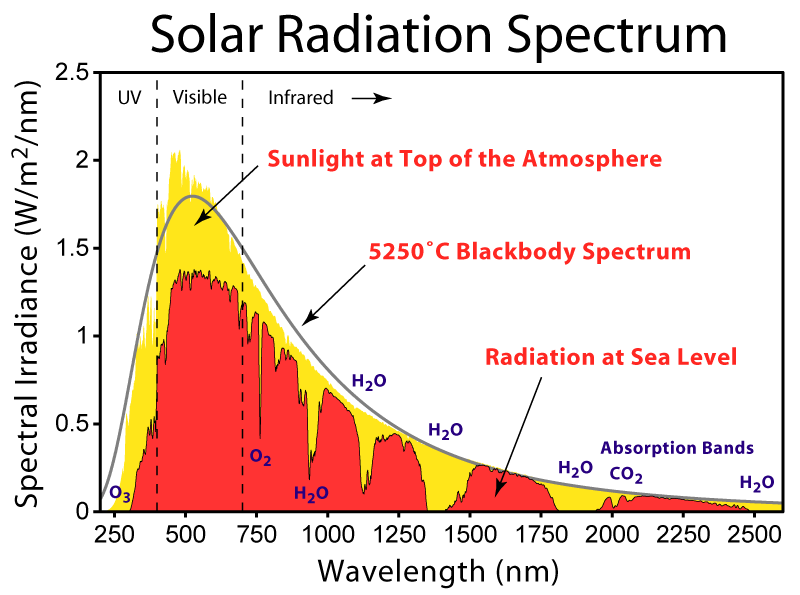
In some fields, such as solar energy and photovoltaics, air mass is indicated by the acronym AM; additionally, the value of the air mass is often given by appending its value to AM, so that AM1 indicates an air mass of 1, AM2 indicates an air mass of 2, and so on. The region above Earth's atmosphere, where there is no atmospheric attenuation of solar radiation, is considered to have " air mass zero" (AM0).

Atmospheric attenuation of solar radiation is not the same for all wavelengths; consequently, passage through the atmosphere not only reduces intensity but also alters the spectral irradiance. Photovoltaic modules are commonly rated using spectral irradiance for an air mass of 1.5 (AM1.5); tables of these standard spectra are given in ASTM G 173-03. The extraterrestrial spectral irradiance (i.e., that for AM0) is given in ASTM E 490-00a.ASTM E 490-00a was reapproved without change in 2006.

For many solar energy applications when high accuracy near the horizon is not required, air mass is commonly determined using the simple secant formula described in the section Plane-parallel atmosphere.

See also

* Air mass (solar energy)
* Atmospheric extinction
* Beer–Lambert–Bouguer law
* Chapman function
* Computation of radiowave attenuation in the atmosphere
* Diffuse sky radiation
* Extinction coefficient
* Illuminance
* International Standard Atmosphere
* Irradiance
* Law of atmospheres
* Light diffusion
* Mie scattering
* Path loss
* Photovoltaic module
* Rayleigh scattering
* Solar irradiation

Notes

References

*
* Optical Telescopes of Today and Tomorrow
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

External links

* Reed Meyer'
downloadable airmass calculator, written in C
(notes in the source code describe the theory in detail)


A source for electronic copies of some of the references.

{{Portal bar, Astronomy, Stars, Spaceflight, Outer space, Solar System

Astronomical imaging
Observational astronomy
Atmospheric optical phenomena