|
Law Of Atmospheres
The barometric formula, sometimes called the ''exponential atmosphere'' or ''isothermal atmosphere'', is a formula used to model how the pressure (or density) of the air changes with altitude. The pressure drops approximately by 11.3 pascals per meter in first 1000 meters above sea level. Pressure equations There are two different equations for computing pressure at various height regimes below 86 km (or 278,400 feet). The first equation is used when the value of standard temperature lapse rate is not equal to zero: P = P_b \left frac\right The second equation is used when standard temperature lapse rate equals zero: P = P_b \exp \left frac\right/math> where: *P_b = reference pressure ( Pa) *T_b = reference temperature ( K) *L_b = temperature lapse rate (K/m) in ISA *h = height at which pressure is calculated (m) *h_b = height of reference level ''b'' (meters; e.g., ''hb'' = 11 000 m) *R^* = universal gas constant: 8.3144598 J/(mol·K) *g_0 = gravitational ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
InHg
Inch of mercury (inHg and ″Hg) is a non- SI unit of measurement for pressure. It is used for barometric pressure in weather reports, refrigeration and aviation in the United States. It is the pressure exerted by a column of mercury in height at the standard acceleration of gravity. Conversion to metric units depends on the temperature of mercury, and hence its density; typical conversion factors are: In older literature, an "inch of mercury" is based on the height of a column of mercury at .Barry N. Taylor, ''Guide for the Use of the International System of Units (SI),'' 1995, NIST Special Publication 811, Appendix /ref> :1 inHg60 °F = In Imperial units: 1 inHg60 °F = 0.489 771 Pounds per square inch, psi, or 2.041 771 inHg60 °F = 1 psi. Applications Aircraft and automobiles Aircraft altimeters measure the relative pressure difference between the lower ambient pressure at altitude and a calibrated reading on the ground. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NRLMSISE-00
NRLMSISE-00 is an empirical, global reference atmospheric model of the Earth from ground to space. It models the temperatures and densities of the atmosphere's components. A primary use of this model is to aid predictions of satellite orbital decay due to atmospheric drag. This model has also been used by astronomers to calculate the mass of air between telescopes and laser beams in order to assess the impact of laser guide stars on the non-lasing telescopes. Development The model, developed by Mike Picone, Alan Hedin, and Doug Drob, is based on the earlier models MSIS-86 and MSISE-90, but updated with actual satellite drag data. It also predicts anomalous oxygen. ''NRL'' stands for the US Naval Research Laboratory. MSIS stands for mass spectrometer and incoherent scatter radar, the two primary data sources for development of earlier versions of the model. ''E'' indicates that the model extends from the ground through exosphere and ''00'' is the year of release. Over the years s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypsometric Equation
The hypsometric equation, also known as the thickness equation, relates an atmospheric pressure ratio to the equivalent thickness of an atmospheric layer considering the layer mean of virtual temperature, gravity, and occasionally wind. It is derived from the hydrostatic equation and the ideal gas law. Formulation The hypsometric equation is expressed as: h = z_2 - z_1 = \frac \, \ln \left(\frac\right), where: *h = thickness of the layer /nowiki>, *z = geometric height /nowiki>, *R = specific gas constant for dry air, *\overline = mean virtual temperature in Kelvin /nowiki>, *g = gravitational acceleration /s2/nowiki>, *p = pressure Pascal_(unit)">Pa.html" ;"title="Pascal_(unit).html" ;"title="/nowiki>Pascal (unit)">Pa">Pascal_(unit).html" ;"title="/nowiki>Pascal (unit)">Pa/nowiki>. In meteorology, p_1 and p_2 are wikt:isobaric, isobaric surfaces. In radiosonde observation, the hypsometric equation can be used to compute the height of a pressure level given the height of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
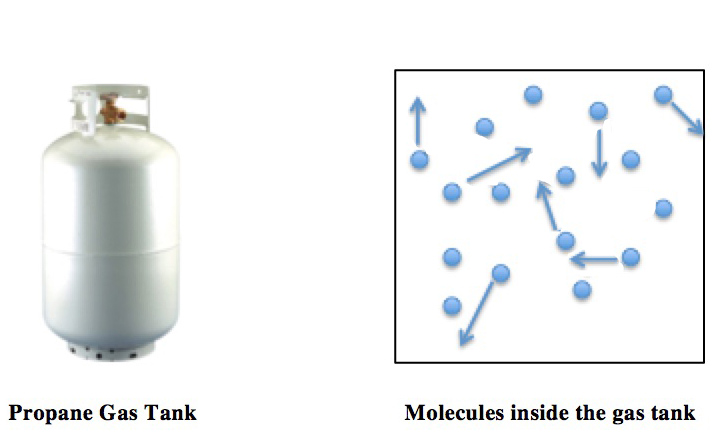
Perfect Gas
In physics and engineering, a perfect gas is a theoretical gas model that differs from real gases in specific ways that makes certain calculations easier to handle. In all perfect gas models, intermolecular forces are neglected. This means that one can neglect many complications that may arise from the Van der Waals forces. All perfect gas models are ideal gas models in the sense that they all follow the ideal gas equation of state. However, the idea of a perfect gas model is often invoked as a combination of the ideal gas equation of state with specific additional assumptions regarding the variation (or nonvariation) of the heat capacity with temperature. Perfect gas nomenclature The terms ''perfect gas'' and ''ideal gas'' are sometimes used interchangeably, depending on the particular field of physics and engineering. Sometimes, other distinctions are made, such as between ''thermally perfect gas'' and ''calorically perfect gas'', or between imperfect, semi-perfect, and perfect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Gas
Real gases are nonideal gases whose molecules occupy space and have interactions; consequently, they do not adhere to the ideal gas law. To understand the behaviour of real gases, the following must be taken into account: *compressibility effects; *variable specific heat capacity; *van der Waals forces; *non-equilibrium thermodynamic effects; *issues with molecular dissociation and elementary reactions with variable composition For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation point of gases, near critical points, at very high pressures, to explain the Joule–Thomson effect, and in other less usual cases. The deviation from ideality can be described by the compressibility factor Z. Models Van der Waals model Real gases are often modeled by taking into account their molar weight and molar volume :RT = \left(p + \frac\ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Troposphere
The troposphere is the first and lowest layer of the atmosphere of the Earth, and contains 75% of the total mass of the planetary atmosphere, 99% of the total mass of water vapour and aerosols, and is where most weather phenomena occur. From the planetary surface of the Earth, the average height of the troposphere is in the tropics; in the middle latitudes; and in the high latitudes of the polar regions in winter; thus the average height of the troposphere is . The term ''troposphere'' derives from the Greek words ''tropos'' (rotating) and '' sphaira'' (sphere) indicating that rotational turbulence mixes the layers of air and so determines the structure and the phenomena of the troposphere. The rotational friction of the troposphere against the planetary surface affects the flow of the air, and so forms the planetary boundary layer (PBL) that varies in height from hundreds of meters up to . The measures of the PBL vary according to the latitude, the landform, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Height
In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter ''H'', is a distance (vertical or radial) over which a physical quantity decreases by a factor of e (the base of natural logarithms, approximately 2.718). Scale height used in a simple atmospheric pressure model For planetary atmospheres, scale height is the increase in altitude for which the atmospheric pressure decreases by a factor of ''e''. The scale height remains constant for a particular temperature. It can be calculated by :H = \frac or equivalently :H = \frac where: * ''k'' = Boltzmann constant = 1.38 x 10−23 J·K−1 * ''R'' = gas constant * ''T'' = mean atmospheric temperature in kelvins = 250 K for Earth * ''m'' = mean mass of a molecule (units kg) * ''M'' = mean mass of one mol of atmospheric particles = 0.029 kg/mol for Earth * ''g'' = acceleration due to gravity at the current location (m/s2) The pressure (force per unit area) at a given alt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an integral assigns numbers to functions in a way that describes Displacement (geometry), displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with Derivative, differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
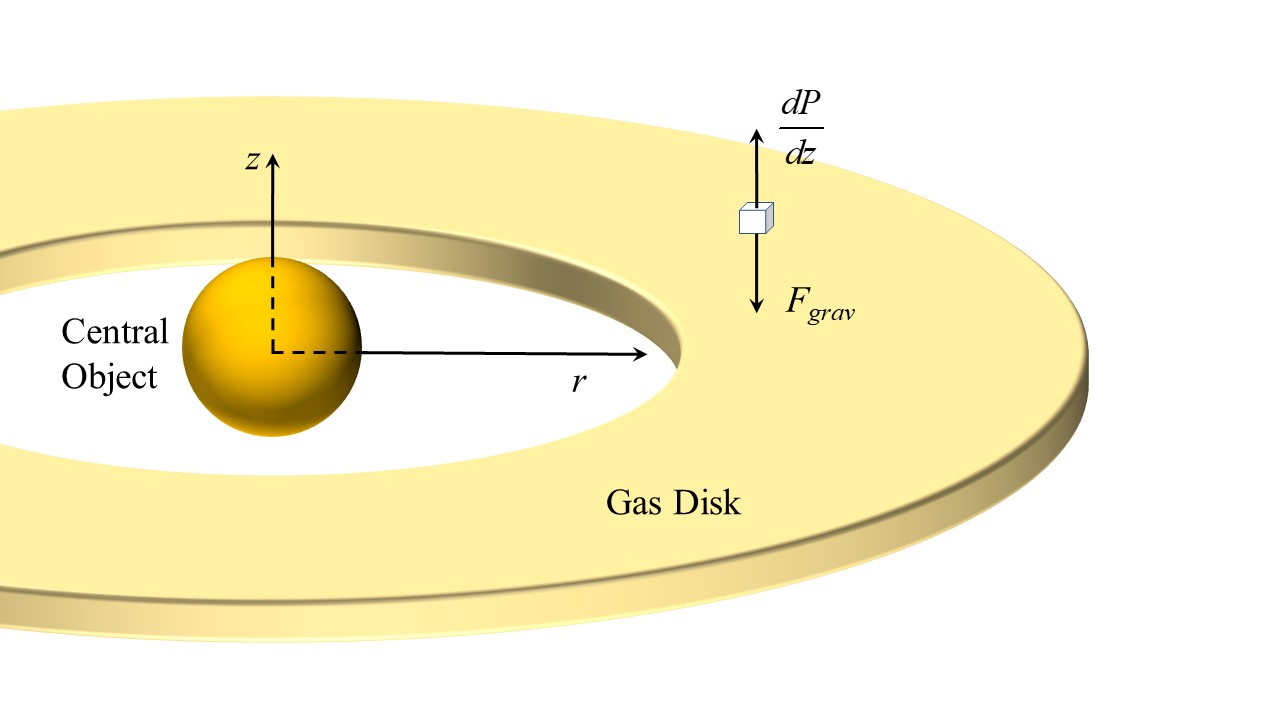
Hydrostatic Pressure
Fluid statics or hydrostatics is the branch of fluid mechanics that studies the condition of the equilibrium of a floating body and submerged body "fluids at hydrostatic equilibrium and the pressure in a fluid, or exerted by a fluid, on an immersed body". It encompasses the study of the conditions under which fluids are at rest in stable equilibrium as opposed to fluid dynamics, the study of fluids in motion. Hydrostatics is a subcategory of fluid statics, which is the study of all fluids, both compressible or incompressible, at rest. Hydrostatics is fundamental to hydraulics, the engineering of equipment for storing, transporting and using fluids. It is also relevant to geophysics and astrophysics (for example, in understanding plate tectonics and the anomalies of the Earth's gravitational field), to meteorology, to medicine (in the context of blood pressure), and many other fields. Hydrostatics offers physical explanations for many phenomena of everyday life, such as why ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |