5-simplex T2 on:
[Wikipedia]
[Google]
[Amazon]
3,3,3,3 symmetry, order 1440. The intersection of these two 5-simplexes is a uniform birectified 5-simplex. = ∩ .
:
Polytopes of Various Dimensions
Jonathan Bowers
{{Polytopes 5-polytopes
In five-dimensional
3,2,3, order 72. It represents joining of 2 orthogonal triangles, orthogonally offset, with all pairs of vertices connected between.
The form ∨∨ has symmetry [2,2,2,_order_48.
These_are_seen_in_the_vertex_figure_
In_geometry,_a_vertex_figure,_broadly_speaking,_is_the_figure_exposed_when_a_corner_of_a_polyhedron_or_polytope_is_sliced_off.
_Definitions
Take_some_corner_or_Vertex_(geometry),_vertex_of_a_polyhedron._Mark_a_point_somewhere_along_each_connect_...
s_of_Bitruncation.html" ;"title=",2,2.html" ;"title="[2,2,2">[2,2,2, order 48.
These are seen in the geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a 5-simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
is a self-dual regular 5-polytope. It has six vertices, 15 edge
Edge or EDGE may refer to:
Technology Computing
* Edge computing, a network load-balancing system
* Edge device, an entry point to a computer network
* Adobe Edge, a graphical development application
* Microsoft Edge, a web browser developed by ...
s, 20 triangle faces
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affe ...
, 15 tetrahedral cells, and 6 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
. It has a dihedral angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the uni ...
of cos−1(), or approximately 78.46°.
The 5-simplex is a solution to the problem: ''Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.''
Alternate names
It can also be called a hexateron, or hexa-5-tope, as a 6- facetted polytope in 5-dimensions. Thename
A name is a term used for identification by an external observer. They can identify a class or category of things, or a single thing, either uniquely, or within a given context. The entity identified by a name is called its referent. A personal ...
''hexateron'' is derived from ''hexa-'' for having six facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
and '' teron'' (with ''ter-'' being a corruption of ''tetra-
Numeral or number prefixes are prefixes derived from numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example:
* unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cyc ...
'') for having four-dimensional facets.
By Jonathan Bowers, a hexateron is given the acronym hix.
As a configuration
This configuration matrix represents the 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.Regular hexateron cartesian coordinates
The ''hexateron'' can be constructed from a5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
by adding a 6th vertex such that it is equidistant from all the other vertices of the 5-cell.
The Cartesian coordinates for the vertices of an origin-centered regular hexateron having edge length 2 are:
:
The vertices of the ''5-simplex'' can be more simply positioned on a hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
in 6-space as permutations of (0,0,0,0,0,1) ''or'' (0,1,1,1,1,1). These construction can be seen as facets of the 6-orthoplex
In geometry, a 6-orthoplex, or 6-cross polytope, is a regular 6-polytope with 12 vertices, 60 edges, 160 triangle faces, 240 tetrahedron cells, 192 5-cell ''4-faces'', and 64 ''5-faces''.
It has two constructed forms, the first being regular wi ...
or rectified 6-cube respectively.
Projected images
Lower symmetry forms
A lower symmetry form is a ''5-cell pyramid'' ( )v, with ,3,3symmetry order 120, constructed as a5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
base in a 4-space hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
, and an apex
The apex is the highest point of something. The word may also refer to:
Arts and media Fictional entities
* Apex (comics), a teenaged super villainess in the Marvel Universe
* Ape-X, a super-intelligent ape in the Squadron Supreme universe
*Apex, ...
point ''above'' the hyperplane. The five ''sides'' of the pyramid are made of 5-cell cells. These are seen as vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s of truncated regular 6-polytopes, like a truncated 6-cube
In six-dimensional geometry, a truncated 6-cube (or truncated hexeract) is a convex uniform 6-polytope, being a truncation of the regular 6-cube.
There are 5 truncations for the 6-cube. Vertices of the truncated 6-cube are located as pairs on the ...
.
Another form is ∨, with ,3,3symmetry order 48, the joining of an orthogonal digon and a tetrahedron, orthogonally offset, with all pairs of vertices connected between. Another form is ∨, with ,2,3
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline ...
symmetry order 36, and extended symmetry vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s of Bitruncation">bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube and a tritruncated 6-simplex. The edge labels here represent the types of face along that direction, and thus represent different edge lengths.
The vertex figure of the omnitruncated 5-simplex honeycomb, , is a 5-simplx with a petrie polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a reg ...
cycle of 5 long edges.
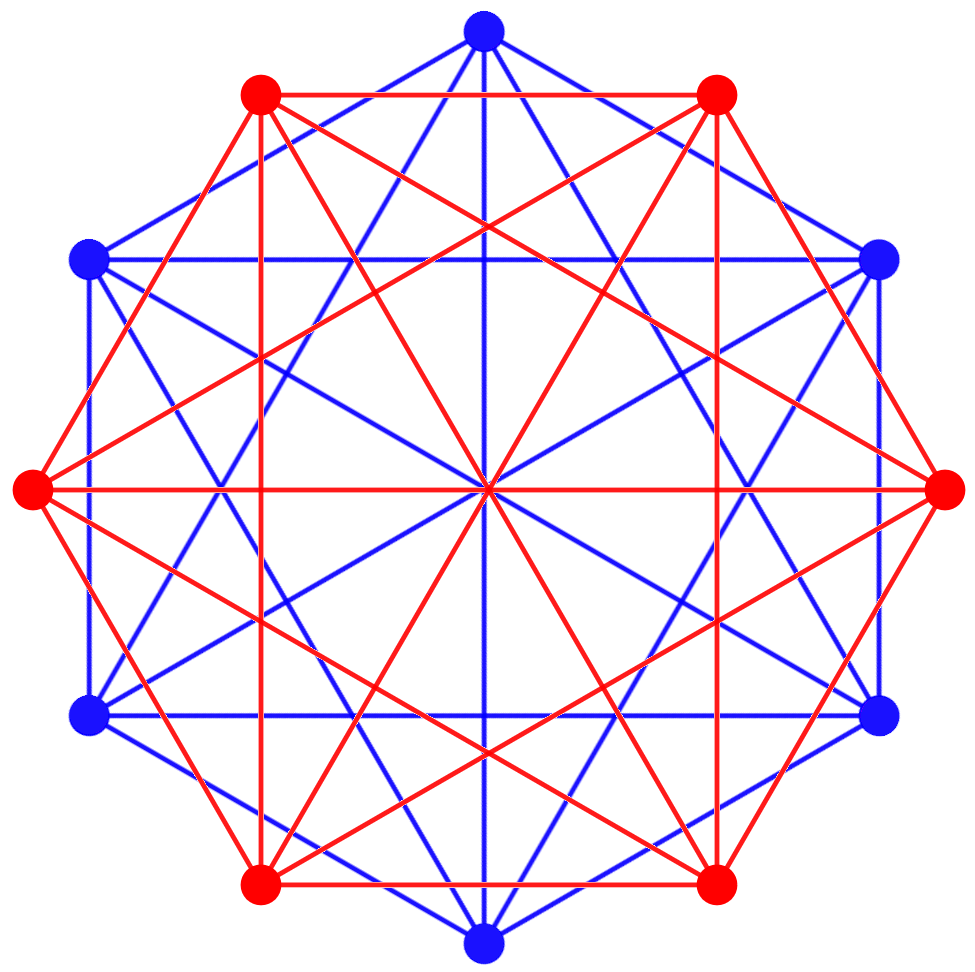
Compound
The compound of two 5-simplexes in dual configurations can be seen in this A6Coxeter plane
In mathematics, the Coxeter number ''h'' is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter.
Definitions
Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there ar ...
projection, with a red and blue 5-simplex vertices and edges. This compound has 
Related uniform 5-polytopes
It is first in a dimensional series of uniform polytopes and honeycombs, expressed byCoxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
as 13k series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune hav ...
.
It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
as 3k1 series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of ''n'' edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat ...
.
The 5-simplex, as 220 polytope is first in dimensional series 22k.
The regular 5-simplex is one of 19 uniform polytera based on the ,3,3,3Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...
, all shown here in A5 Coxeter plane
In mathematics, the Coxeter number ''h'' is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter.
Definitions
Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there ar ...
orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in ...
s. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
See also
*11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedr ...
Notes
References
* * Coxeter, H.S.M.: ** ** *** (Paper 22) *** (Paper 23) *** (Paper 24) * * **External links
*Polytopes of Various Dimensions
Jonathan Bowers
{{Polytopes 5-polytopes