2004 Drama Films on:
[Wikipedia]
[Google]
[Amazon]
_
_
In_Buddhism,_nirodha,_"cessation,"_"extinction,"_or_"suppression,"_refers_to_the_cessation_or_renouncing_of_craving_and_desire._It_is_the_third_of_the__Four_Noble_Truths,_stating_that_suffering_(_dukkha)_ceases_when_craving_and_desire_are_renoun_...
,_Noble_Eightfold_Path.html" "title="ukkha,_Pratītyasamutpāda">Samudaya,_Nirvana.html" "title="Pratītyasamutpāda.html" ;"title="Dukkha.html" ;"title="Four Noble Truths: BUDDHIST PHILOSOPHY Encycl ...
4 (four) is a

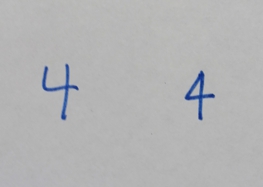
 .
.
 On the
On the
_–_Dukkha,_Pratītyasamutpāda">Samudaya,_Nirvana">Nirodhanumber
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
, numeral and digit. It is the natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''cardinal ...
following 3 and preceding 5. It is the smallest semiprime
In mathematics, a semiprime is a natural number that is the product of exactly two prime numbers. The two primes in the product may equal each other, so the semiprimes include the squares of prime numbers.
Because there are infinitely many prime ...
and composite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
, and is considered unlucky in many East Asian cultures.
In mathematics
Four is the smallestcomposite number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Equivalently, it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime, ...
, its proper divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
s being and . Four is the sum and product of two
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultur ...
with itself: + = = x , the only number such that + = = x , which also makes four the smallest squared prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. In Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976.
In his 1947 paper, R. L. Goodstein introduced the specific sequence of operations that are now called ''hyperoperati ...
, , and so forth, for any number of up arrows. By consequence, four is the only square one more than a prime number, specifically three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
. The sum of the first four prime numbers two
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultur ...
+ three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
+ five + seven is the only sum of four consecutive prime numbers that yields an odd prime number, seventeen, which is the fourth super-prime. Four lies between the first proper pair of twin primes, three
3 is a number, numeral, and glyph.
3, three, or III may also refer to:
* AD 3, the third year of the AD era
* 3 BC, the third year before the AD era
* March, the third month
Books
* '' Three of Them'' (Russian: ', literally, "three"), a 1901 ...
and five, which are the first two Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 429496 ...
s, like seventeen, which is the third. On the other hand, the square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90- degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length a ...
of four 42, equivalently the fourth power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So:
:''n''4 = ''n'' × ''n'' × ''n'' × ''n''
Fourth powers are also formed by multiplying a number by its cube. Further ...
of two 24, is sixteen; the only number that has = as a form of factorization
In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several ''factors'', usually smaller or simpler objects of the same kind ...
. Holistically, there are four elementary arithmetic operations in mathematics: addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
(+), subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
(−), multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
(×), and division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
(÷); and four basic number system
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
s, the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real ...
s , rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
s , integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s , and natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''cardinal ...
s .
Each natural number divisible by 4 is a difference of squares of two natural numbers, i.e. = − . A number is a multiple of 4 if its last two digits are a multiple of 4. For example, 1092 is a multiple of 4 because .
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that every natural number can be represented as the sum of four integer squares. That is, the squares form an additive basis of order four.
p = a_0^2 + a_1^2 + a_2^2 + a_ ...
states that every positive integer can be written as the sum of at most four square number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
s. Three are not always sufficient; for instance cannot be written as the sum of three squares.
There are four all-Harshad number
In mathematics, a harshad number (or Niven number) in a given number base is an integer that is divisible by the sum of its digits when written in that base.
Harshad numbers in base are also known as -harshad (or -Niven) numbers.
Harshad number ...
s: 1, 2, ''4'', and 6. 12, which is divisible by four thrice over, is a Harshad number in all bases except octal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, ...
.
A four-sided plane figure is a quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
or quadrangle, sometimes also called a ''tetragon''. It can be further classified as a rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
or ''oblong'', kite
A kite is a tethered heavier than air flight, heavier-than-air or lighter-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. ...
, rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The ...
, and square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
.
Four is the highest degree general polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation' ...
for which there is a solution in radicals
A solution in radicals or algebraic solution is a closed-form expression, and more specifically a closed-form algebraic expression, that is the solution of a polynomial equation, and relies only on addition, subtraction, multiplication, divi ...
.
The four-color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions sha ...
states that a planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross ...
(or, equivalently, a flat map
A map is a symbolic depiction emphasizing relationships between elements of some space, such as objects, regions, or themes.
Many maps are static, fixed to paper or some other durable medium, while others are dynamic or interactive. Although ...
of two-dimensional regions such as countries) can be colored using four colors, so that adjacent vertices (or regions) are always different colors. Three colors are not, in general, sufficient to guarantee this. The largest planar complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is c ...
has four vertices.
A solid figure with four faces as well as four vertices is a tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, which is the smallest possible number of faces and vertices a polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on th ...
can have. The regular tetrahedron, also called a 3-simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
, is the simplest Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
. It has four regular triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each ...
s as faces that are themselves at dual positions with the vertices of another tetrahedron. Tetrahedra can be inscribed inside all other four Platonic solids, and tessellate space alongside the regular octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...
in the alternated cubic honeycomb
The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.
Other names incl ...
.
Four-dimensional space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
is the highest-dimensional space featuring more than three regular convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
figures:
*Two-dimensional: infinitely many regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
s.
*Three-dimensional: five regular polyhedra
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equival ...
; the five Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
s which are the tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
, octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at ea ...
, dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
, and icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
.
*Four-dimensional: six regular polychora
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six convex and ten star regu ...
; the 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
, 8-cell or tesseract
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eig ...
, 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mi ...
, 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, heca ...
, and 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
. The 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, made of regular octahedra
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet a ...
, has no analogue in any other dimension; it is self-dual
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a Injective function, one-to-one fashion, often (but not always) by means of an Involution (mathematics), involutio ...
, with its 24-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular polytope, regular space-filling tessellation (or honeycomb (geometry), honeycomb) of 4-dimensional Euclidean space by ...
dual to the 16-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensiona ...
.
*Five-dimensional and every higher dimension: three regular convex -polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
s, all within the infinite family of regular -simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
es, -hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
s, and - orthoplexes.
The fourth dimension is also the highest dimension where regular self-intersecting figures exist:
*Two-dimensional: infinitaly many regular star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations ...
s.
*Three-dimensional: ''four'' regular star polyhedra
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
There are two general kinds of star polyhedron:
*Polyhedra which self-intersect in a repetitive way.
*Concave p ...
, the regular Kepler-Poinsot star polyhedra.
*Four-dimensional: ten regular star polychora, the Schläfli–Hess star polychora. They contain cells of Kepler-Poinsot polyhedra alongside regular tetrahedra, icosahedra
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
and dodecahedra
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
.
*Five-dimensional and every higher dimension: zero regular star-polytopes; uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, se ...
star polytopes in dimensions > are the most symmetric, which mainly originate from stellations of regular -polytopes.
Altogether, sixteen (or 16 = 42) regular convex and star polychora are generated from symmetries of ''four'' (4) Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections th ...
s and point groups
In geometry, a point group is a mathematical group of symmetry operations ( isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every ...
in the fourth dimension: the simplex, hypercube, icositetrachoric, and hexacosichoric groups; with the demihypercube
In geometry, demihypercubes (also called ''n-demicubes'', ''n-hemicubes'', and ''half measure polytopes'') are a class of ''n''- polytopes constructed from alternation of an ''n''- hypercube, labeled as ''hγn'' for being ''half'' of the hy ...
group generating two alternative constructions.
There are also sixty-four (or 64 = 43) four-dimensional Bravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n ...
s, ''and'' sixty-four uniform polychora in the fourth dimension based on the same , , and Coxeter groups
In mathematics, a Coxeter group, named after Harold Scott MacDonald Coxeter, H. S. M. Coxeter, is an group (mathematics), abstract group that admits a group presentation, formal description in terms of Reflection (mathematics), reflections (or Kal ...
, and extending to prismatic groups of uniform polyhedra
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent.
Uniform polyhedra may be regular (if also fa ...
, including one special non-Wythoffian form, the grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope ...
. There are also two infinite families of duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
s and antiprismatic prisms in the fourth dimension.
Four-dimensional differential manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ma ...
s have some unique properties. There is only one differential structure In mathematics, an ''n''-dimensional differential structure (or differentiable structure) on a set ''M'' makes ''M'' into an ''n''-dimensional differential manifold, which is a topological manifold with some additional structure that allows for diff ...
on except when = , in which case there are uncountably many.
The smallest non-cyclic group
In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bina ...
has four elements; it is the Klein four-group
In mathematics, the Klein four-group is a Group (mathematics), group with four elements, in which each element is Involution (mathematics), self-inverse (composing it with itself produces the identity)
and in which composing any two of the three ...
. ''A'' alternating group
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or
Basic prop ...
s are not simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
for values ≤ .
Further extensions of the real numbers under Hurwitz's theorem states that there are four normed division algebras: the real numbers , the complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
, the quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
s , and the octonion
In mathematics, the octonions are a normed division algebra over the real numbers, a kind of hypercomplex number system. The octonions are usually represented by the capital letter O, using boldface or blackboard bold \mathbb O. Octonions have e ...
s . Under Cayley–Dickson construction
In mathematics, the Cayley–Dickson construction, named after Arthur Cayley and Leonard Eugene Dickson, produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one. The algebras produced b ...
s, the sedenion
In abstract algebra, the sedenions form a 16-dimensional noncommutative and nonassociative algebra over the real numbers; they are obtained by applying the Cayley–Dickson construction to the octonions, and as such the octonions are isomorphic to ...
s constitute a further fourth extension over . The real numbers are ordered, commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name o ...
and associative algebras
In mathematics, an algebra over a field (often simply called an algebra) is a vector space equipped with a bilinear product. Thus, an algebra is an algebraic structure consisting of a set together with operations of multiplication and addition ...
, as well as alternative algebra In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have
*x(xy) = (xx)y
*(yx)x = y(xx)
for all ''x'' and ''y'' in the algebra.
Every associative algebra is ...
s with power-associativity In mathematics, specifically in abstract algebra, power associativity is a property of a binary operation that is a weak form of associativity.
Definition
An algebra over a field, algebra (or more generally a magma (algebra), magma) is said to be ...
. The complex numbers share all four multiplicative algebraic properties of the reals , without being ordered. The quaternions loose a further commutative algebraic property, while holding associative, alternative, and power-associative properties. The octonions are alternative and power-associative, while the sedenions are only power-associative. The sedenions and all further ''extensions'' of these four normed division algebras are solely power-associative with non-trivial zero divisor
In abstract algebra, an element of a ring is called a left zero divisor if there exists a nonzero in such that , or equivalently if the map from to that sends to is not injective. Similarly, an element of a ring is called a right zero ...
s, which makes them non-division algebras. has a vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can ...
of dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
1, while , , and work in algebraic number field
In mathematics, an algebraic number field (or simply number field) is an extension field K of the field of rational numbers such that the field extension K / \mathbb has finite degree (and hence is an algebraic field extension).
Thus K is a f ...
s of dimensions 2, 4, 8, and 16, respectively.
List of basic calculations
Evolution of the Hindu-Arabic digit

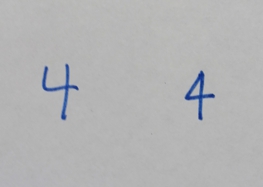
Brahmic numerals
The Brahmi numerals are a numeral system attested from the 3rd century BCE (somewhat later in the case of most of the tens). They are a non positional decimal system. They are the direct graphic ancestors of the modern Hindu–Arabic numeral s ...
represented 1, 2, and 3 with as many lines. 4 was simplified by joining its four lines into a cross that looks like the modern plus sign. The Shunga
is a type of Japanese erotic art typically executed as a kind of ukiyo-e, often in woodblock print format. While rare, there are also extant erotic painted handscrolls which predate ukiyo-e. Translated literally, the Japanese word ''shunga' ...
would add a horizontal line on top of the digit, and the Kshatrapa and Pallava evolved the digit to a point where the speed of writing was a secondary concern. The Arab
The Arabs (singular: Arab; singular ar, عَرَبِيٌّ, DIN 31635: , , plural ar, عَرَب, DIN 31635: , Arabic pronunciation: ), also known as the Arab people, are an ethnic group mainly inhabiting the Arab world in Western Asia, ...
s' 4 still had the early concept of the cross, but for the sake of efficiency, was made in one stroke by connecting the "western" end to the "northern" end; the "eastern" end was finished off with a curve. The Europeans dropped the finishing curve and gradually made the digit less cursive, ending up with a digit very close to the original Brahmin cross.
While the shape of the character for the digit 4 has an ascender in most modern typeface
A typeface (or font family) is the design of lettering that can include variations in size, weight (e.g. bold), slope (e.g. italic), width (e.g. condensed), and so on. Each of these variations of the typeface is a font.
There are list of type ...
s, in typefaces with text figures
Text figures (also known as non-lining, lowercase, old style, ranging, hanging, medieval, billing, or antique figures or numerals) are numerals designed with varying heights in a fashion that resembles a typical line of running text, hence the ...
the glyph usually has a descender
In typography and handwriting, a descender is the portion of a letter that extends below the baseline of a font.
For example, in the letter ''y'', the descender is the "tail", or that portion of the diagonal line which lies below the ''v'' c ...
, as, for example, in seven-segment display
A seven-segment display is a form of electronic display device for displaying decimal numerals that is an alternative to the more complex dot matrix displays.
Seven-segment displays are widely used in digital clocks, electronic meters, basic ...
s of pocket calculators and digital watches, as well as certain optical character recognition
Optical character recognition or optical character reader (OCR) is the electronic or mechanical conversion of images of typed, handwritten or printed text into machine-encoded text, whether from a scanned document, a photo of a document, a scen ...
fonts, 4 is seen with an open top.
Television station
A television station is a set of equipment managed by a business, organisation or other entity, such as an amateur television (ATV) operator, that transmits video content and audio content via radio waves directly from a transmitter on the earth ...
s that operate on channel 4
Channel 4 is a British free-to-air public broadcast television network operated by the state-owned enterprise, state-owned Channel Four Television Corporation. It began its transmission on 2 November 1982 and was established to provide a four ...
have occasionally made use of another variation of the "open 4", with the open portion being on the side, rather than the top. This version resembles the Canadian Aboriginal syllabics letter ᔦ. The magnetic ink character recognition
Magnetic ink character recognition code, known in short as MICR code, is a character recognition technology used mainly by the banking industry to streamline the processing and clearance of cheques and other documents. MICR encoding, called the ' ...
"CMC-7" font also uses this variety of "4".
In religion
Buddhism
*Four Noble Truths
In Buddhism, the Four Noble Truths (Sanskrit: ; pi, cattāri ariyasaccāni; "The four Arya satyas") are "the truths of the Noble Ones", the truths or realities for the "spiritually worthy ones". Four_Noble_Truths:_BUDDHIST_PHILOSOPHY_Encycl_...
_–_Dukkha,__–_[Samudaya,_Nirvana.html"__"title="Pratītyasamutpāda.html"_;"title="Dukkha.html"_;"title="Four_Noble_Truths:_BUDDHIST_PHILOSOPHY_Encycl_...
_–_Dukkha">Four_Noble_Truths:_BUDDHIST_PHILOSOPHY_Encycl_...– Dukkha">Four Noble Truths: BUDDHIST PHILOSOPHY Encycl ...
– Dukkha, Pratītyasamutpāda">Samudaya, Nirvana">Nirodha In Buddhism, nirodha, "cessation," "extinction," or "suppression," refers to the cessation or renouncing of craving and desire. It is the third of the Four Noble Truths, stating that suffering ( dukkha) ceases when craving and desire are renoun ...
, Noble Eightfold Path">Magga The Buddhist path (''marga'') to liberation, also referred to as awakening, is described in a wide variety of ways. The classical one is the Noble Eightfold Path, which is only one of several summaries presented in the Sutta Pitaka. A number of ...
*Four sights – observations which affected Prince Siddhartha deeply and made him realize the sufferings of all beings, and compelled him to begin his spiritual journey—an old age, old man, a illness, sick man, a death, dead man, and an
ascetic
Asceticism (; from the el, ἄσκησις, áskesis, exercise', 'training) is a lifestyle characterized by abstinence from sensual pleasures, often for the purpose of pursuing spiritual goals. Ascetics may withdraw from the world for their p ...
* Four Great Elements – earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
, water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as a ...
, fire
Fire is the rapid oxidation of a material (the fuel) in the exothermic chemical process of combustion, releasing heat, light, and various reaction Product (chemistry), products.
At a certain point in the combustion reaction, called the ignition ...
, and wind
Wind is the natural movement of air or other gases relative to a planet's surface. Winds occur on a range of scales, from thunderstorm flows lasting tens of minutes, to local breezes generated by heating of land surfaces and lasting a few hou ...
*Four Heavenly Kings
The Four Heavenly Kings are four Buddhist gods, each of whom is believed to watch over one cardinal direction of the world. In Chinese mythology, they are known collectively as the "Fēng Tiáo Yǔ Shùn" () or "Sìdà Tiānwáng" (). In the a ...
* Four Foundations of Mindfulness – contemplation of the body, contemplation of feelings, contemplation of mind, contemplation of mental objects
*Four Right Exertions
The Four Right Exertions (also known as, Four Proper Exertions, Four Right Efforts, Four Great Efforts, Four Right Endeavors or Four Right Strivings) (Pali: '; Skt.: ' or ') are an integral part of the Buddhist path to Enlightenment (understan ...
* Four Bases of Power
* Four jhānas
* Four arūpajhānas
* Four Divine Abidings – loving-kindness Loving-kindness may refer to:
* an English translation of Chesed
( he, חֶסֶד, also Romanized: ) is a Hebrew word that means 'kindness or love between people', specifically of the devotional piety of people towards God as well as of love o ...
, compassion
Compassion motivates people to go out of their way to relieve the physical, mental or emotional pains of others and themselves. Compassion is often regarded as being sensitive to the emotional aspects of the suffering of others. When based on n ...
, sympathetic joy, and equanimity
Equanimity (Latin: ''æquanimitas'', having an even mind; ''aequus'' even; ''animus'' mind/soul) is a state of inner peace, psychological stability and composure which is undisturbed by experience of or exposure to emotions, pain, or other phenom ...
*Four stages of enlightenment
The four stages of awakening in Early Buddhism and Theravada
are four progressive stages culminating in full awakening ('' Bodhi'') as an Arahant (SN 22.122).
These four stages are Sotāpanna, Sakadāgāmi, Anāgāmi, and Arahant. The oldest B ...
– stream-enterer, once-returner
In Buddhism, the Sakadāgāmin (Pali; Sanskrit: ''Sakṛdāgāmin'', ), "returning once"Rhys Davids & Stede (1921-25), p. 660, entry for "Sakadāgāmin" (retrieved 26 Sep 2007 at http://dsal.uchicago.edu/cgi-bin/philologic/getobject.pl?c.3:1:2653. ...
, non-returner, and arahant
In Buddhism, an ''arhat'' (Sanskrit: अर्हत्) or ''arahant'' (Pali: अरहन्त्, 𑀅𑀭𑀳𑀦𑁆𑀢𑁆) is one who has gained insight into the true nature of existence and has achieved ''Nirvana'' and liberated ...
* Four main pilgrimage sites – Lumbini
Lumbinī ( ne, लुम्बिनी, IPA=ˈlumbini , "the lovely") is a Buddhist pilgrimage site in the Rupandehi District of Lumbini Province in Nepal. It is the place where, according to Buddhist tradition, Queen Mahamayadevi gave birth ...
, Bodh Gaya, Sarnath
Sarnath (Hindustani pronunciation: aːɾnaːtʰ also referred to as Sarangnath, Isipatana, Rishipattana, Migadaya, or Mrigadava) is a place located northeast of Varanasi, near the confluence of the Ganges and the Varuna rivers in Uttar Pr ...
, and Kusinara
Kushinagar ( Hindustani: or ; Pali: ; Sanskrit: ) is a town in the Kushinagar district in Uttar Pradesh, India. It is an important and popular Buddhist pilgrimage site, where Buddhists believe Gautama Buddha attained ''parinirvana''.
Etymo ...
Judeo-Christian symbolism
*TheTetragrammaton
The Tetragrammaton (; ), or Tetragram, is the four-letter Hebrew language, Hebrew theonym (transliterated as YHWH), the name of God in the Hebrew Bible. The four letters, written and read from right to left (in Hebrew), are ''yodh'', ''he (l ...
is the four-letter name of God
In monotheism, monotheistic thought, God is usually viewed as the supreme being, creator deity, creator, and principal object of Faith#Religious views, faith.Richard Swinburne, Swinburne, R.G. "God" in Ted Honderich, Honderich, Ted. (ed)''The Ox ...
.
*Ezekiel
Ezekiel (; he, יְחֶזְקֵאל ''Yəḥezqēʾl'' ; in the Septuagint written in grc-koi, Ἰεζεκιήλ ) is the central protagonist of the Book of Ezekiel in the Hebrew Bible.
In Judaism, Christianity, and Islam, Ezekiel is acknow ...
has a vision of four living creatures
In biology, an organism () is any living system that functions as an individual entity. All organisms are composed of cells (cell theory). Organisms are classified by taxonomy into groups such as multicellular animals, plants, and fungi; ...
: a man, a lion, an ox, and an eagle.
*The four Matriarchs (foremothers) of Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
are Sarah
Sarah (born Sarai) is a biblical matriarch and prophetess, a major figure in Abrahamic religions. While different Abrahamic faiths portray her differently, Judaism, Christianity, and Islam all depict her character similarly, as that of a piou ...
, Rebekah
Rebecca, ; Syriac: , ) from the Hebrew (lit., 'connection'), from Semitic root , 'to tie, couple or join', 'to secure', or 'to snare') () appears in the Hebrew Bible as the wife of Isaac and the mother of Jacob and Esau. According to biblical ...
, Leah
Leah ''La'ya;'' from (; ) appears in the Hebrew Bible as one of the two wives of the Biblical patriarch Jacob. Leah was Jacob's first wife, and the older sister of his second (and favored) wife Rachel. She is the mother of Jacob's first son ...
, and Rachel
Rachel () was a Biblical figure, the favorite of Jacob's two wives, and the mother of Joseph and Benjamin, two of the twelve progenitors of the tribes of Israel. Rachel's father was Laban. Her older sister was Leah, Jacob's first wife. Her aun ...
.
*The Four Species (lulav
''Lulav'' (; he, לולב) is a closed frond of the date palm tree. It is one of the Four Species used during the Jewish holiday of Sukkot. The other Species are the '' hadass'' ( myrtle), '' aravah'' (willow), and ''etrog'' (citron). When ...
, hadass
Hadass (Hebrew: הדס, pl. ''hadassim'' - הדסים) is a branch of the myrtle tree that forms part of the lulav used on the Jewish holiday of Sukkot.
Hadass is one of the Four species (''arba'ah minim''–ארבעת המינים). T ...
, aravah and etrog
Etrog ( he, אֶתְרוֹג, plural: '; Ashkenazi Hebrew: ', plural: ') is the yellow citron or ''Citrus medica'' used by Jews during the week-long holiday of Sukkot as one of the four species. Together with the ''lulav'', ''hadass'', and '' a ...
) are taken as one of the mitzvot
In its primary meaning, the Hebrew word (; he, מִצְוָה, ''mīṣvā'' , plural ''mīṣvōt'' ; "commandment") refers to a commandment commanded by God to be performed as a religious duty. Jewish law () in large part consists of discus ...
on the Jewish
Jews ( he, יְהוּדִים, , ) or Jewish people are an ethnoreligious group and nation originating from the Israelites Israelite origins and kingdom: "The first act in the long drama of Jewish history is the age of the Israelites""The ...
holiday of Sukkot
or ("Booths, Tabernacles")
, observedby = Jews, Samaritans, a few Protestant denominations, Messianic Jews, Semitic Neopagans
, type = Jewish, Samaritan
, begins = 15th day of Tishrei
, ends = 21st day of Tishre ...
. (Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
)
*The Four Cups of Wine to drink on the Jewish
Jews ( he, יְהוּדִים, , ) or Jewish people are an ethnoreligious group and nation originating from the Israelites Israelite origins and kingdom: "The first act in the long drama of Jewish history is the age of the Israelites""The ...
holiday of Passover
Passover, also called Pesach (; ), is a major Jewish holidays, Jewish holiday that celebrates the The Exodus, Biblical story of the Israelites escape from slavery in Ancient Egypt, Egypt, which occurs on the 15th day of the Hebrew calendar, He ...
. (Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
)
*The Four Questions to be asked on the Jewish
Jews ( he, יְהוּדִים, , ) or Jewish people are an ethnoreligious group and nation originating from the Israelites Israelite origins and kingdom: "The first act in the long drama of Jewish history is the age of the Israelites""The ...
holiday of Passover
Passover, also called Pesach (; ), is a major Jewish holidays, Jewish holiday that celebrates the The Exodus, Biblical story of the Israelites escape from slavery in Ancient Egypt, Egypt, which occurs on the 15th day of the Hebrew calendar, He ...
. (Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
)
*The Four Sons to be dealt with on the Jewish
Jews ( he, יְהוּדִים, , ) or Jewish people are an ethnoreligious group and nation originating from the Israelites Israelite origins and kingdom: "The first act in the long drama of Jewish history is the age of the Israelites""The ...
holiday of Passover
Passover, also called Pesach (; ), is a major Jewish holidays, Jewish holiday that celebrates the The Exodus, Biblical story of the Israelites escape from slavery in Ancient Egypt, Egypt, which occurs on the 15th day of the Hebrew calendar, He ...
. (Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
)
*The Four Expressions of Redemption to be said on the Jewish
Jews ( he, יְהוּדִים, , ) or Jewish people are an ethnoreligious group and nation originating from the Israelites Israelite origins and kingdom: "The first act in the long drama of Jewish history is the age of the Israelites""The ...
holiday of Passover
Passover, also called Pesach (; ), is a major Jewish holidays, Jewish holiday that celebrates the The Exodus, Biblical story of the Israelites escape from slavery in Ancient Egypt, Egypt, which occurs on the 15th day of the Hebrew calendar, He ...
. (Judaism
Judaism ( he, ''Yahăḏūṯ'') is an Abrahamic, monotheistic, and ethnic religion comprising the collective religious, cultural, and legal tradition and civilization of the Jewish people. It has its roots as an organized religion in the ...
)
*The four Gospel
Gospel originally meant the Christian message ("the gospel"), but in the 2nd century it came to be used also for the books in which the message was set out. In this sense a gospel can be defined as a loose-knit, episodic narrative of the words an ...
s: Matthew
Matthew may refer to:
* Matthew (given name)
* Matthew (surname)
* ''Matthew'' (ship), the replica of the ship sailed by John Cabot in 1497
* ''Matthew'' (album), a 2000 album by rapper Kool Keith
* Matthew (elm cultivar), a cultivar of the Ch ...
, Mark
Mark may refer to:
Currency
* Bosnia and Herzegovina convertible mark, the currency of Bosnia and Herzegovina
* East German mark, the currency of the German Democratic Republic
* Estonian mark, the currency of Estonia between 1918 and 1927
* F ...
, Luke
People
*Luke (given name), a masculine given name (including a list of people and characters with the name)
*Luke (surname) (including a list of people and characters with the name)
*Luke the Evangelist, author of the Gospel of Luke. Also known as ...
, and John
John is a common English name and surname:
* John (given name)
* John (surname)
John may also refer to:
New Testament
Works
* Gospel of John, a title often shortened to John
* First Epistle of John, often shortened to 1 John
* Secon ...
. (Christianity
Christianity is an Abrahamic monotheistic religion based on the life and teachings of Jesus of Nazareth. It is the world's largest and most widespread religion with roughly 2.38 billion followers representing one-third of the global pop ...
)
*The Four Horsemen of the Apocalypse
The Four Horsemen of the Apocalypse are figures in the Christian scriptures, first appearing in the Book of Revelation, a piece of apocalypse literature written by John of Patmos.
Revelation 6 tells of a book or scroll in God's right hand tha ...
ride in the Book of Revelation
The Book of Revelation is the final book of the New Testament (and consequently the final book of the Christian Bible). Its title is derived from the first word of the Koine Greek text: , meaning "unveiling" or "revelation". The Book of R ...
. (Christianity
Christianity is an Abrahamic monotheistic religion based on the life and teachings of Jesus of Nazareth. It is the world's largest and most widespread religion with roughly 2.38 billion followers representing one-third of the global pop ...
)
*The four holy cities of Judaism: Jerusalem
Jerusalem (; he, יְרוּשָׁלַיִם ; ar, القُدس ) (combining the Biblical and common usage Arabic names); grc, Ἱερουσαλήμ/Ἰεροσόλυμα, Hierousalḗm/Hierosóluma; hy, Երուսաղեմ, Erusałēm. i ...
, Hebron
Hebron ( ar, الخليل or ; he, חֶבְרוֹן ) is a Palestinian. city in the southern West Bank, south of Jerusalem. Nestled in the Judaean Mountains, it lies above sea level. The second-largest city in the West Bank (after East J ...
, Safed
Safed (known in Hebrew language, Hebrew as Tzfat; Sephardi Hebrew, Sephardic Hebrew & Modern Hebrew: צְפַת ''Tsfat'', Ashkenazi Hebrew pronunciation, Ashkenazi Hebrew: ''Tzfas'', Biblical Hebrew: ''Ṣǝp̄aṯ''; ar, صفد, ''Ṣafad''), i ...
, and Tiberius
Tiberius Julius Caesar Augustus (; 16 November 42 BC – 16 March AD 37) was the second Roman emperor. He reigned from AD 14 until 37, succeeding his stepfather, the first Roman emperor Augustus. Tiberius was born in Rome in 42 BC. His father ...
Hinduism
*There are fourVedas
upright=1.2, The Vedas are ancient Sanskrit texts of Hinduism. Above: A page from the '' Atharvaveda''.
The Vedas (, , ) are a large body of religious texts originating in ancient India. Composed in Vedic Sanskrit, the texts constitute the ...
: Rigveda, Samaveda, Yajurveda and Atharvaveda.
*In Puruṣārtha
''Purushartha'' (Sanskrit: पुरुषार्थ, International Alphabet of Sanskrit Transliteration, IAST: ) literally means "object(ive) of men".Dharma
Dharma (; sa, धर्म, dharma, ; pi, dhamma, italic=yes) is a key concept with multiple meanings in Indian religions, such as Hinduism, Buddhism, Jainism, Sikhism and others. Although there is no direct single-word translation for '' ...
, Artha
''Artha'' (; sa, अर्थ; Tamil: ''poruḷ'' / ''பொருள்'') is one of the four aims of human life in Indian philosophy.James Lochtefeld (2002), The Illustrated Encyclopedia of Hinduism, Rosen Publishing, New York, , pp 55–56 T ...
, Kāma
''Kama'' (Sanskrit ) means "desire, wish, longing" in Hindu texts, Hindu, Buddhist texts, Buddhist, Jain literature, Jain, and Sikh literature, Sikh literature.Monier Williamsकाम, kāmaMonier-Williams Sanskrit English Dictionary, pp 27 ...
, Moksha
''Moksha'' (; sa, मोक्ष, '), also called ''vimoksha'', ''vimukti'' and ''mukti'', is a term in Hinduism, Buddhism, Jainism and Sikhism for various forms of emancipation, enlightenment, liberation, and release. In its soteriology, ...
.
*The four stages of life Brahmacharya
''Brahmacharya'' (; sa, ब्रह्मचर्य ) is a concept within Indian religions that literally means to stay in conduct within one's own Self. In Yoga, Hinduism, Buddhism and Jainism it generally refers to a lifestyle charac ...
(student life), Grihastha (household life), Vanaprastha (retired life) and Sannyasa
''Sannyasa'' (Sanskrit: संन्यास; IAST: ), sometimes spelled Sanyasa (सन्न्यास) or Sanyasi (for the person), is life of renunciation and the fourth stage within the Hindu system of four life stages known as '' As ...
(renunciation).
*The four primary castes or strata of society: Brahmana
The Brahmanas (; Sanskrit: , ''Brāhmaṇam'') are Vedic śruti works attached to the Samhitas (hymns and mantras) of the Rig, Sama, Yajur, and Atharva Vedas. They are a secondary layer or classification of Sanskrit texts embedded within ea ...
(priest/teacher), Kshatriya
Kshatriya ( hi, क्षत्रिय) (from Sanskrit ''kṣatra'', "rule, authority") is one of the four varna (social orders) of Hindu society, associated with warrior aristocracy. The Sanskrit term ''kṣatriyaḥ'' is used in the con ...
(warrior/politician), Vaishya
Vaishya (Sanskrit: वैश्य, ''vaiśya'') is one of the four Varna (Hinduism), varnas of the Hinduism, Hindu social order in India. Vaishyas are classed third in the order of caste hierarchy.
The occupation of Vaishyas consists mainly ...
(landowner/entrepreneur) and Shudra
Shudra or ''Shoodra'' (Sanskrit: ') is one of the four '' varnas'' of the Hindu caste system and social order in ancient India. Various sources translate it into English as a caste, or alternatively as a social class. Theoretically, class ser ...
(servant/manual laborer).
*The swastika
The swastika (卐 or 卍) is an ancient religious and cultural symbol, predominantly in various Eurasian, as well as some African and American cultures, now also widely recognized for its appropriation by the Nazi Party and by neo-Nazis. It ...
symbol is traditionally used in Hindu
Hindus (; ) are people who religiously adhere to Hinduism.Jeffery D. Long (2007), A Vision for Hinduism, IB Tauris, , pages 35–37 Historically, the term has also been used as a geographical, cultural, and later religious identifier for ...
religions as a sign of good luck and signifies good from all four directions.
*The god Brahma
Brahma ( sa, ब्रह्मा, Brahmā) is a Hindu god, referred to as "the Creator" within the Trimurti, the trinity of supreme divinity that includes Vishnu, and Shiva.Jan Gonda (1969)The Hindu Trinity Anthropos, Bd 63/64, H 1/2, pp. 21 ...
has four faces.
*There are four ''yuga
A ''yuga'', in Hinduism, is generally used to indicate an age of time.
In the ''Rigveda'', a ''yuga'' refers to generations, a long period, a very brief period, or a yoke (joining of two things). In the ''Mahabharata'', the words ''yuga'' and ...
s'': '' Satya'', '' Dvapara'', ''Treta
''Treta Yuga'', in Hinduism, is the second and second best of the four '' yugas'' (world ages) in a ''Yuga Cycle'', preceded by '' Krita (Satya) Yuga'' and followed by '' Dvapara Yuga''. ''Treta Yuga'' lasts for 1,296,000 years (3,600 divine year ...
'' and ''Kali
Kali (; sa, काली, ), also referred to as Mahakali, Bhadrakali, and Kalika ( sa, कालिका), is a Hinduism, Hindu goddess who is considered to be the goddess of ultimate power, time, destruction and change in Shaktism. In t ...
''
Islam
*Eid al-Adha
Eid al-Adha () is the second and the larger of the two main holidays celebrated in Islam (the other being Eid al-Fitr). It honours the willingness of Ibrahim (Abraham) to sacrifice his son Ismail (Ishmael) as an act of obedience to Allah's co ...
lasts for four days, from the 10th to the 14th of Dhul Hijja
Dhu al-Hijja ( ar, ذُو ٱلْحِجَّة, translit=Ḏū al-Ḥijja, ), also spelled Zu al-Hijja, is the twelfth and final month in the Islamic calendar. It is a very sacred month in the Islamic calendar, one in which the '' Ḥajj'' (Pilgri ...
.
*The four holy cities of Islam: Mecca, Medina, Jerusalem and Damascus.
*The four tombs in the Green Dome: Muhammad, Abu Bakr, Umar ibn Khattab and Isa ibn Maryam (Jesus).
*There are four Rashidun
, image = تخطيط كلمة الخلفاء الراشدون.png
, caption = Calligraphic representation of Rashidun Caliphs
, birth_place = Mecca, Hejaz, Arabia present-day Saudi Arabia
, known_for = Companions of t ...
or Rightly Guided Caliph
A caliphate or khilāfah ( ar, خِلَافَة, ) is an institution or public office under the leadership of an Islamic steward with the title of caliph (; ar, خَلِيفَة , ), a person considered a political-religious successor to th ...
s: Abu Bakr
Abu Bakr Abdallah ibn Uthman Abi Quhafa (; – 23 August 634) was the senior companion and was, through his daughter Aisha, a father-in-law of the Islamic prophet Muhammad, as well as the first caliph of Islam. He is known with the honor ...
, Umar ibn al-Khattab
ʿUmar ibn al-Khaṭṭāb ( ar, عمر بن الخطاب, also spelled Omar, ) was the second Rashidun caliph, ruling from August 634 until his assassination in 644. He succeeded Abu Bakr () as the second caliph of the Rashidun Caliphate o ...
, Uthman ibn Affan
Uthman ibn Affan ( ar, عثمان بن عفان, ʿUthmān ibn ʿAffān; – 17 June 656), also spelled by Colloquial Arabic, Turkish and Persian rendering Osman, was a second cousin, son-in-law and notable companion of the Islamic prop ...
and Ali ibn Abi Talib
ʿAlī ibn Abī Ṭālib ( ar, عَلِيّ بْن أَبِي طَالِب; 600 – 661 CE) was the last of four Rightly Guided Caliphs to rule Islam (r. 656 – 661) immediately after the death of Muhammad, and he was the first Shia Imam. ...
.
*The Four Arch Angels in Islam are: Jibraeel (Gabriel), Mikaeel (Michael), Izraeel (Azrael), and Israfil (Raphael)
*There are four months in which war is not permitted: Muharram
Muḥarram ( ar, ٱلْمُحَرَّم) (fully known as Muharram ul Haram) is the first month of the Islamic calendar. It is one of the four sacred months of the year when warfare is forbidden. It is held to be the second holiest month after R ...
, Rajab
Rajab ( ar, رَجَب) is the seventh month of the Islamic calendar. The lexical definition of the classical Arabic verb ''rajaba'' is "to respect" which could also mean "be awe or be in fear", of which Rajab is a derivative.
This month is re ...
, Dhu al-Qi'dah
Dhu al-Qa'dah ( ar, ذُو ٱلْقَعْدَة, ', ), also spelled Dhu al-Qi'dah or Zu al-Qa'dah, is the eleventh month in the Islamic calendar.
It could possibly mean "possessor or owner of the sitting and seating place" - the space occupied w ...
and Dhu al-Hijjah
Dhu al-Hijja ( ar, ذُو ٱلْحِجَّة, translit=Ḏū al-Ḥijja, ), also spelled Zu al-Hijja, is the twelfth and final month in the Islamic calendar. It is a very sacred month in the Islamic calendar, one in which the ''Hajj, Ḥajj'' (P ...
.
*There are four Sunni
Sunni Islam () is the largest branch of Islam, followed by 85–90% of the world's Muslims. Its name comes from the word '' Sunnah'', referring to the tradition of Muhammad. The differences between Sunni and Shia Muslims arose from a disagr ...
schools of fiqh
''Fiqh'' (; ar, فقه ) is Islamic jurisprudence. Muhammad-> Companions-> Followers-> Fiqh.
The commands and prohibitions chosen by God were revealed through the agency of the Prophet in both the Quran and the Sunnah (words, deeds, and ...
: Hanafi
The Hanafi school ( ar, حَنَفِية, translit=Ḥanafiyah; also called Hanafite in English), Hanafism, or the Hanafi fiqh, is the oldest and one of the four traditional major Sunni schools ( maddhab) of Islamic Law (Fiqh). It is named aft ...
, Shafi`i
The Shafii ( ar, شَافِعِي, translit=Shāfiʿī, also spelled Shafei) school, also known as Madhhab al-Shāfiʿī, is one of the four major traditional schools of religious law (madhhab) in the Sunnī branch of Islam. It was founded by ...
, Maliki
The ( ar, مَالِكِي) school is one of the four major schools of Islamic jurisprudence within Sunni Islam. It was founded by Malik ibn Anas in the 8th century. The Maliki school of jurisprudence relies on the Quran and hadiths as primary ...
and Hanbali
The Hanbali school ( ar, ٱلْمَذْهَب ٱلْحَنۢبَلِي, al-maḏhab al-ḥanbalī) is one of the four major traditional Sunni schools (''madhahib'') of Islamic jurisprudence. It is named after the Arab scholar Ahmad ibn Hanbal ...
.
*There are four major Sunni Imams: Abū Ḥanīfa
Nuʿmān ibn Thābit ibn Zūṭā ibn Marzubān ( ar, نعمان بن ثابت بن زوطا بن مرزبان; –767), commonly known by his '' kunya'' Abū Ḥanīfa ( ar, أبو حنيفة), or reverently as Imam Abū Ḥanīfa by Sunni Musl ...
, Muhammad ibn Idris ash-Shafi`i
Abū ʿAbdillāh Muḥammad ibn Idrīs al-Shāfiʿī ( ar, أَبُو عَبْدِ ٱللهِ مُحَمَّدُ بْنُ إِدْرِيسَ ٱلشَّافِعِيُّ, 767–19 January 820 CE) was an Arab Muslim theologian, writer, and schola ...
, Malik ibn Anas
Malik ibn Anas ( ar, مَالِك بن أَنَس, 711–795 CE / 93–179 AH), whose full name is Mālik bin Anas bin Mālik bin Abī ʿĀmir bin ʿAmr bin Al-Ḥārith bin Ghaymān bin Khuthayn bin ʿAmr bin Al-Ḥārith al-Aṣbaḥī ...
and Ahmad ibn Hanbal
Ahmad ibn Hanbal al-Dhuhli ( ar, أَحْمَد بْن حَنْبَل الذهلي, translit=Aḥmad ibn Ḥanbal al-Dhuhlī; November 780 – 2 August 855 CE/164–241 AH), was a Muslim jurist, theologian, ascetic, hadith traditionist, and ...
.
*There are four books in Islam: Taurait, Zaboor, Injeel, Quran.
*Waiting for four months is ordained for those who take an oath for abstention from their wives.
*The waiting period of the woman whose husband dies is four months and ten days.
*When Abraham said: "My Lord, show me how You give life to the dead," Allah said: "Why! Do you have no faith?" Abraham replied: "Yes, but in order that my heart be at rest." He said: "Then take four birds, and tame them to yourself, then put a part of them on every hill, and summon them; they will come to you flying. l-Baqara 2:260*The respite of four months was granted to give time to the mushriks in Surah At-Tawba
At-Tawbah ( ar, ٱلتوبة, ; The Repentance), also known as Bara'ah ( ar, براءة, ; Repudiation), is the ninth chapter ('' sūrah'') of the Quran. It contains 129 verses ('' āyāt'') and is one of the last Medinan surahs.
This Surah i ...
so that they should consider their position carefully and decide whether to make preparation for war or to emigrate from the country or to accept Islam.
*Those who accuse honorable women (of unchastity) but do not produce four witnesses, flog them with eighty lashes, and do not admit their testimony ever after. They are indeed transgressors. n-Noor 24:4Taoism
*Four Symbols
The Four Symbols (, literally meaning "four images"), are four mythological creatures appearing among the Chinese constellations along the ecliptic, and viewed as the guardians of the four cardinal directions. These four creatures are also ref ...
of I Ching
The ''I Ching'' or ''Yi Jing'' (, ), usually translated ''Book of Changes'' or ''Classic of Changes'', is an ancient Chinese divination text that is among the oldest of the Chinese classics. Originally a divination manual in the Western Zho ...
Other
*In a more general sense, numerous mythological and cosmogonical systems considerFour corners of the world
Several cosmological and mythological systems portray four corners of the world or four quarters of the world corresponding approximately to the four points of the compass (or the two solstices and two equinoxes). At the center may lie a sacr ...
as essentially corresponding to the four points of the compass.
*Four is the sacred number of the Zia
Zia or ZIA (also spelled Ziya, Ḍiya , Dia or Diya) may refer to:
People
* Zia (name), including a list of people and fictional characters with the name
** A romanization of the Wu ( Shanghainese) pronunciation of the Chinese surname Xie (謝)
...
, an indigenous tribe located in the U.S. state of New Mexico
)
, population_demonym = New Mexican ( es, Neomexicano, Neomejicano, Nuevo Mexicano)
, seat = Santa Fe
, LargestCity = Albuquerque
, LargestMetro = Tiguex
, OfficialLang = None
, Languages = English, Spanish ( New Mexican), Navajo, Ker ...
.
*The Chinese, the Koreans, and the Japanese are superstitious about the number four because it is a homonym
In linguistics, homonyms are words which are homographs (words that share the same spelling, regardless of pronunciation), or homophones (equivocal words, that share the same pronunciation, regardless of spelling), or both. Using this definition, ...
for "death" in their languages.
*In Slavic mythology
Slavic mythology or Slavic religion is the religious beliefs, myths, and ritual practices of the Slavs before Christianisation, which occurred at various stages between the 8th and the 13th century. The South Slavs, who likely settled in the B ...
, the god Svetovid has four heads.
In politics
*Four Freedoms
The Four Freedoms were goals articulated by U.S. President Franklin D. Roosevelt on Monday, January 6, 1941. In an address known as the Four Freedoms speech (technically the 1941 State of the Union address), he proposed four fundamental freed ...
: four fundamental freedoms that Franklin D. Roosevelt
Franklin Delano Roosevelt (; ; January 30, 1882April 12, 1945), often referred to by his initials FDR, was an American politician and attorney who served as the 32nd president of the United States from 1933 until his death in 1945. As the ...
declared ought to be enjoyed by everyone in the world: Freedom of Speech, Freedom of Religion, Freedom from Want, Freedom from Fear.
* Gang of Four: Popular name for four Chinese Communist Party leaders who rose to prominence during China's Cultural Revolution, but were ousted in 1976 following the death of Chairman Mao Zedong
Mao Zedong pronounced ; also romanised traditionally as Mao Tse-tung. (26 December 1893 – 9 September 1976), also known as Chairman Mao, was a Chinese communist revolutionary who was the founder of the People's Republic of China (PRC) ...
. Among the four was Mao's widow, Jiang Qing
Jiang Qing (19 March 191414 May 1991), also known as Madame Mao, was a Chinese communist revolutionary, actress, and major political figure during the Cultural Revolution (1966–1976). She was the fourth wife of Mao Zedong, the Chairman o ...
. Since then, many other political factions headed by four people have been called "Gangs of Four".
In computing
*Fourbit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represente ...
s (half a byte
The byte is a unit of digital information that most commonly consists of eight bits. Historically, the byte was the number of bits used to encode a single character of text in a computer and for this reason it is the smallest addressable unit ...
) are sometimes called a nibble
In computing, a nibble (occasionally nybble, nyble, or nybl to match the spelling of byte) is a four-bit aggregation, or half an octet. It is also known as half-byte or tetrade. In a networking or telecommunication context, the nibble is oft ...
.
In science
*Atetramer
A tetramer () (''tetra-'', "four" + '' -mer'', "parts") is an oligomer formed from four monomers or subunits. The associated property is called ''tetramery''. An example from inorganic chemistry is titanium methoxide with the empirical formula Ti ...
is an oligomer
In chemistry and biochemistry, an oligomer () is a molecule that consists of a few repeating units which could be derived, actually or conceptually, from smaller molecules, monomers.Quote: ''Oligomer molecule: A molecule of intermediate relativ ...
formed out of four sub-units.
In astronomy
*Four terrestrial (or rocky) planets in theSolar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar S ...
: Mercury
Mercury commonly refers to:
* Mercury (planet), the nearest planet to the Sun
* Mercury (element), a metallic chemical element with the symbol Hg
* Mercury (mythology), a Roman god
Mercury or The Mercury may also refer to:
Companies
* Merc ...
, Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never fa ...
, Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
, and Mars
Mars is the fourth planet from the Sun and the second-smallest planet in the Solar System, only being larger than Mercury (planet), Mercury. In the English language, Mars is named for the Mars (mythology), Roman god of war. Mars is a terr ...
.
*Four giant gas/ice planets in the Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar S ...
: Jupiter
Jupiter is the fifth planet from the Sun and the List of Solar System objects by size, largest in the Solar System. It is a gas giant with a mass more than two and a half times that of all the other planets in the Solar System combined, but ...
, Saturn
Saturn is the sixth planet from the Sun and the second-largest in the Solar System, after Jupiter. It is a gas giant with an average radius of about nine and a half times that of Earth. It has only one-eighth the average density of Earth; h ...
, Uranus
Uranus is the seventh planet from the Sun. Its name is a reference to the Greek god of the sky, Uranus (mythology), Uranus (Caelus), who, according to Greek mythology, was the great-grandfather of Ares (Mars (mythology), Mars), grandfather ...
, and Neptune
Neptune is the eighth planet from the Sun and the farthest known planet in the Solar System. It is the fourth-largest planet in the Solar System by diameter, the third-most-massive planet, and the densest giant planet. It is 17 times ...
.
*Four of Jupiter's moons (the Galilean moons
The Galilean moons (), or Galilean satellites, are the four largest moons of Jupiter: Io, Europa, Ganymede, and Callisto. They were first seen by Galileo Galilei in December 1609 or January 1610, and recognized by him as satellites of Jupiter ...
) are readily visible from Earth with a hobby telescope.
*Messier object
The Messier objects are a set of 110 astronomical objects catalogued by the French astronomer Charles Messier in his ''Catalogue des Nébuleuses et des Amas d'Étoiles'' (''Catalogue of Nebulae and Star Clusters'').
Because Messier was only int ...
M4, a magnitude 7.5 globular cluster
A globular cluster is a spheroidal conglomeration of stars. Globular clusters are bound together by gravity, with a higher concentration of stars towards their centers. They can contain anywhere from tens of thousands to many millions of membe ...
in the constellation Scorpius
Scorpius is a zodiac constellation located in the Southern celestial hemisphere, where it sits near the center of the Milky Way, between Libra to the west and Sagittarius to the east. Scorpius is an ancient constellation that pre-dates the Gre ...
.
*The Roman numeral IV stands for subgiant
A subgiant is a star that is brighter than a normal main-sequence star of the same spectral class, but not as bright as giant stars. The term subgiant is applied both to a particular spectral luminosity class and to a stage in the evolution ...
in the Yerkes spectral classification scheme
In astronomy, stellar classification is the classification of stars based on their stellar spectrum, spectral characteristics. Electromagnetic radiation from the star is analyzed by splitting it with a Prism (optics), prism or diffraction grati ...
.
In biology
*Four is the number ofnucleobase
Nucleobases, also known as ''nitrogenous bases'' or often simply ''bases'', are nitrogen-containing biological compounds that form nucleosides, which, in turn, are components of nucleotides, with all of these monomers constituting the basic b ...
types in DNA and RNA
Ribonucleic acid (RNA) is a polymeric molecule essential in various biological roles in coding, decoding, regulation and expression of genes. RNA and deoxyribonucleic acid ( DNA) are nucleic acids. Along with lipids, proteins, and carbohydra ...
– adenine
Adenine () ( symbol A or Ade) is a nucleobase (a purine derivative). It is one of the four nucleobases in the nucleic acid of DNA that are represented by the letters G–C–A–T. The three others are guanine, cytosine and thymine. Its derivati ...
, guanine
Guanine () ( symbol G or Gua) is one of the four main nucleobases found in the nucleic acids DNA and RNA, the others being adenine, cytosine, and thymine (uracil in RNA). In DNA, guanine is paired with cytosine. The guanine nucleoside is called ...
, cytosine
Cytosine () ( symbol C or Cyt) is one of the four nucleobases found in DNA and RNA, along with adenine, guanine, and thymine (uracil in RNA). It is a pyrimidine derivative, with a heterocyclic aromatic ring and two substituents attached (an am ...
, thymine
Thymine () ( symbol T or Thy) is one of the four nucleobases in the nucleic acid of DNA that are represented by the letters G–C–A–T. The others are adenine, guanine, and cytosine. Thymine is also known as 5-methyluracil, a pyrimidine nu ...
(uracil
Uracil () (symbol U or Ura) is one of the four nucleobases in the nucleic acid RNA. The others are adenine (A), cytosine (C), and guanine (G). In RNA, uracil binds to adenine via two hydrogen bonds. In DNA, the uracil nucleobase is replaced by ...
in RNA
Ribonucleic acid (RNA) is a polymeric molecule essential in various biological roles in coding, decoding, regulation and expression of genes. RNA and deoxyribonucleic acid ( DNA) are nucleic acids. Along with lipids, proteins, and carbohydra ...
).
*Many chordate
A chordate () is an animal of the phylum Chordata (). All chordates possess, at some point during their larval or adult stages, five synapomorphies, or primary physical characteristics, that distinguish them from all the other taxa. These fiv ...
s have four feet, legs or leglike appendages (tetrapods
Tetrapods (; ) are four-limbed vertebrate animals constituting the superclass Tetrapoda (). It includes extant and extinct amphibians, sauropsids (reptiles, including dinosaurs and therefore birds) and synapsids (pelycosaurs, extinct therapsids ...
).
*The mammal
Mammals () are a group of vertebrate animals constituting the class Mammalia (), characterized by the presence of mammary glands which in females produce milk for feeding (nursing) their young, a neocortex (a region of the brain), fur or ...
ian heart
The heart is a muscular organ in most animals. This organ pumps blood through the blood vessels of the circulatory system. The pumped blood carries oxygen and nutrients to the body, while carrying metabolic waste such as carbon dioxide t ...
consists of four chambers.
*Many mammal
Mammals () are a group of vertebrate animals constituting the class Mammalia (), characterized by the presence of mammary glands which in females produce milk for feeding (nursing) their young, a neocortex (a region of the brain), fur or ...
s (Carnivora
Carnivora is a Clade, monophyletic order of Placentalia, placental mammals consisting of the most recent common ancestor of all felidae, cat-like and canidae, dog-like animals, and all descendants of that ancestor. Members of this group are f ...
, Ungulata
Ungulates ( ) are members of the diverse clade Ungulata which primarily consists of large mammals with hooves. These include odd-toed ungulates such as horses, rhinoceroses, and tapirs; and even-toed ungulates such as cattle, pigs, giraffes, ...
) use four fingers for movement.
*All insect
Insects (from Latin ') are pancrustacean hexapod invertebrates of the class Insecta. They are the largest group within the arthropod phylum. Insects have a chitinous exoskeleton, a three-part body ( head, thorax and abdomen), three pairs ...
s with wings except flies
Flies are insects of the order Diptera, the name being derived from the Greek δι- ''di-'' "two", and πτερόν ''pteron'' "wing". Insects of this order use only a single pair of wings to fly, the hindwings having evolved into advanced ...
and some others have four wing
A wing is a type of fin that produces lift while moving through air or some other fluid. Accordingly, wings have streamlined cross-sections that are subject to aerodynamic forces and act as airfoils. A wing's aerodynamic efficiency is expres ...
s.
*Insects of the superorder Endopterygota
Endopterygota (from Ancient Greek ''endon'' 'inner' + ''pterón'' 'wing' + New Latin ''-ota'' 'having'), also known as Holometabola, is a superorder of insects within the infraclass Neoptera that go through distinctive larval, pupal, and adult s ...
, also known as Holometabola, such as butterflies, ants, bees, beetles, fleas, flies, moths, and wasps, undergo holometabolism
Holometabolism, also called complete metamorphosis, is a form of insect development which includes four life stages: egg, larva, pupa, and imago (or adult). Holometabolism is a synapomorphic trait of all insects in the superorder Endopterygot ...
—complete metamorphism in four stages—from (1) embryo (ovum, egg), to (2) larva (such as grub, caterpillar), then (3) pupa (such as the chrysalis), and finally (4) the imago.
*In the common ABO blood group system
The ABO blood group system is used to denote the presence of one, both, or neither of the A and B antigens on erythrocytes. For human blood transfusions, it is the most important of the 43 different blood type (or group) classification system ...
, there are four blood types (A, B, O, AB).
*Humans
Humans (''Homo sapiens'') are the most abundant and widespread species of primate, characterized by bipedalism and exceptional cognitive skills due to a large and complex brain. This has enabled the development of advanced tools, culture, ...
have four canines
Canine may refer to:
Zoology and anatomy
* a dog-like Canid animal in the subfamily Caninae
** ''Canis'', a genus including dogs, wolves, coyotes, and jackals
** Dog, the domestic dog
* Canine tooth, in mammalian oral anatomy
People with the surn ...
and four wisdom teeth
A third molar, commonly called wisdom tooth, is one of the three molars per quadrant of the human dentition. It is the most posterior of the three. The age at which wisdom teeth come through ( erupt) is variable, but this generally occurs betw ...
.
*The cow's stomach is divided in four digestive compartments: reticulum, rumen, omasum and abomasum.
In chemistry
* Valency ofcarbon
Carbon () is a chemical element with the symbol C and atomic number 6. It is nonmetallic and tetravalent
In chemistry, the valence (US spelling) or valency (British spelling) of an element is the measure of its combining capacity with o ...
(that is basis of life on the Earth) is four. Also because of its tetrahedral crystal bond structure, diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Another solid form of carbon known as graphite is the Chemical stability, chemically stable form of car ...
(one of the natural allotropes of carbon) is the hardest known naturally occurring material. It is also the valence of silicon
Silicon is a chemical element with the symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic luster, and is a tetravalent metalloid and semiconductor. It is a member of group 14 in the periodic tab ...
, whose compounds form the majority of the mass of the Earth's crust.
*The atomic number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every ...
of beryllium
Beryllium is a chemical element with the symbol Be and atomic number 4. It is a steel-gray, strong, lightweight and brittle alkaline earth metal. It is a divalent element that occurs naturally only in combination with other elements to form mi ...
*There are four basic states of matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic partic ...
: solid
Solid is one of the State of matter#Four fundamental states, four fundamental states of matter (the others being liquid, gas, and Plasma (physics), plasma). The molecules in a solid are closely packed together and contain the least amount o ...
, liquid
A liquid is a nearly incompressible fluid that conforms to the shape of its container but retains a (nearly) constant volume independent of pressure. As such, it is one of the four fundamental states of matter (the others being solid, gas, a ...
, gas
Gas is one of the four fundamental states of matter (the others being solid, liquid, and plasma).
A pure gas may be made up of individual atoms (e.g. a noble gas like neon), elemental molecules made from one type of atom (e.g. oxygen), or ...
, and plasma
Plasma or plasm may refer to:
Science
* Plasma (physics), one of the four fundamental states of matter
* Plasma (mineral), a green translucent silica mineral
* Quark–gluon plasma, a state of matter in quantum chromodynamics
Biology
* Blood pla ...
.
In physics
*Special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws o ...
and general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
treat nature as four-dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
al: 3D regular space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually consider ...
and one-dimensional time
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, to ...
are treated together and called spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
. Also, any event ''E'' has a light cone
In special and general relativity, a light cone (or "null cone") is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take thro ...
composed of four zones of possible communication and cause and effect (outside the light cone is strictly incommunicado).
*There are four fundamental forces
In physics, the fundamental interactions, also known as fundamental forces, are the interactions that do not appear to be reducible to more basic interactions. There are four fundamental interactions known to exist: the gravitational and electro ...
(electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of a ...
, gravitation
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stron ...
, the weak nuclear force
In nuclear physics and particle physics, the weak interaction, which is also often called the weak force or weak nuclear force, is one of the four known fundamental interactions, with the others being electromagnetism, the strong interaction, ...
, and the strong nuclear force
The strong interaction or strong force is a fundamental interaction that confines quarks into proton, neutron, and other hadron particles. The strong interaction also binds neutrons and protons to create atomic nuclei, where it is called the n ...
).
*In statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic be ...
, the four functions inequality is an inequality for four functions on a finite distributive lattice
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set uni ...
.
In logic and philosophy
 *The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The
*The symbolic meanings of the number four are linked to those of the cross and the square. "Almost from prehistoric times, the number four was employed to signify what was solid, what could be touched and felt. Its relationship to the cross (four points) made it an outstanding symbol of wholeness and universality, a symbol which drew all to itself". Where lines of latitude and longitude intersect, they divide the earth into four proportions. Throughout the world kings and chieftains have been called "lord of the four suns" or "lord of the four quarters of the earth", which is understood to refer to the extent of their powers both territorially and in terms of total control of their subjects' doings.
*The Square of Opposition
In term logic (a branch of philosophical logic), the square of opposition is a diagram representing the relations between the four basic categorical propositions.
The origin of the square can be traced back to Aristotle's tractate ''On Interpre ...
, in both its Aristotelian version and its Boolean version, consists of four forms: A ("All ''S'' is ''R''"), I ("Some ''S'' is ''R''"), E ("No ''S'' is ''R''"), and O ("Some ''S'' is not ''R''").
*In regard to whether two given propositions can have the same truth value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values (''true'' or '' false'').
Computing
In some progr ...
, there are four separate logical possibilities: the propositions are ''subalterns'' (possibly both are true, and possibly both are false); ''subcontraries'' (both may be true, but not that both are false); ''contraries'' (both may be false, but not that both are true); or ''contradictories'' (it is not possible that both are true, and it is not possible that both are false).
*Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
held that there are basically four causes
The four causes or four explanations are, in Aristotelian thought, four fundamental types of answer to the question "why?", in analysis of change or movement in nature: the material, the formal, the efficient, and the final. Aristotle wrote th ...
in nature: the material
Material is a substance or mixture of substances that constitutes an object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical and chemical properties, or on their geologi ...
, the formal, the efficient, and the final
Final, Finals or The Final may refer to:
*Final (competition), the last or championship round of a sporting competition, match, game, or other contest which decides a winner for an event
** Another term for playoffs, describing a sequence of cont ...
.
*The Stoics
Stoicism is a school of Hellenistic philosophy founded by Zeno of Citium in Athens in the early 3rd century BCE. It is a philosophy of personal virtue ethics informed by its system of logic and its views on the natural world, asserting that th ...
held with four basic categories
Category, plural categories, may refer to:
Philosophy and general uses
*Categorization, categories in cognitive science, information science and generally
*Category of being
*Categories (Aristotle), ''Categories'' (Aristotle)
*Category (Kant)
...
, all viewed as bodies (substantial and insubstantial): (1) ''substance'' in the sense of substrate, primary formless matter; (2) ''quality'', matter's organization to differentiate and individualize something, and coming down to a physical ingredient such as ''pneuma'', breath; (3) ''somehow holding'' (or ''disposed''), as in a posture, state, shape, size, action, and (4) ''somehow holding'' (or ''disposed'') ''toward something,'' as in relative location, familial relation, and so forth.
*Immanuel Kant
Immanuel Kant (, , ; 22 April 1724 – 12 February 1804) was a German philosopher and one of the central Enlightenment thinkers. Born in Königsberg, Kant's comprehensive and systematic works in epistemology, metaphysics, ethics, and ...
expounded a table of judgments involving four three-way alternatives, in regard to (1) Quantity, (2) Quality, (3) Relation, (4) Modality, and, based thereupon, a table of four categories, named by the terms just listed, and each with three subcategories.
*Arthur Schopenhauer
Arthur Schopenhauer ( , ; 22 February 1788 – 21 September 1860) was a German philosopher. He is best known for his 1818 work ''The World as Will and Representation'' (expanded in 1844), which characterizes the phenomenal world as the prod ...
's doctoral thesis was ''On the Fourfold Root of the Principle of Sufficient Reason
''On the Fourfold Root of the Principle of Sufficient Reason'' (german: Ueber die vierfache Wurzel des Satzes vom zureichenden Grunde) is an elaboration on the classical Principle of Sufficient Reason, written by German philosopher Arthur Schope ...
''.
*Franz Brentano
Franz Clemens Honoratus Hermann Josef Brentano (; ; 16 January 1838 – 17 March 1917) was an influential German philosopher, psychologist, and former Catholic priest (withdrawn in 1873 due to the definition of papal infallibility in matters of F ...
held that any major philosophical period has four phases: (1) Creative and rapidly progressing with scientific interest and results; then declining through the remaining phases, (2) practical, (3) increasingly skeptical, and (4) literary, mystical, and scientifically worthless—until philosophy is renewed through a new period's first phase. (See Brentano's essay "The Four Phases of Philosophy and Its Current State" 1895, tr. by Mezei and Smith 1998.)
*C. S. Peirce
Charles Sanders Peirce ( ; September 10, 1839 – April 19, 1914) was an American philosopher, logician, mathematician and scientist who is sometimes known as "the father of pragmatism".
Educated as a chemist and employed as a scientist for t ...
, usually a trichotomist, discussed four methods for overcoming troublesome uncertainties and achieving secure beliefs: (1) the method of tenacity (policy of sticking to initial belief), (2) the method of authority, (3) the method of congruity (following a fashionable paradigm
In science and philosophy, a paradigm () is a distinct set of concepts or thought patterns, including theories, research methods, postulates, and standards for what constitute legitimate contributions to a field.
Etymology
''Paradigm'' comes f ...
), and (4) the fallibilistic, self-correcting method of science (see " The Fixation of Belief", 1877); and four barriers to inquiry, barriers refused by the fallibilist: (1) assertion of absolute certainty; (2) maintaining that something is unknowable; (3) maintaining that something is inexplicable because absolutely basic or ultimate; (4) holding that perfect exactitude is possible, especially such as to quite preclude unusual and anomalous phenomena (seeF.R.L.
irst Rule of Logic 1899). * Paul Weiss built a system involving four modes of being: Actualities (substances in the sense of substantial, spatiotemporally finite beings), Ideality or Possibility (pure normative form), Existence (the dynamic field), and God (unity). (See Weiss's ''Modes of Being'', 1958). *
Karl Popper
Sir Karl Raimund Popper (28 July 1902 – 17 September 1994) was an Austrian-British philosopher, academic and social commentator. One of the 20th century's most influential philosophers of science, Popper is known for his rejection of the cl ...
outlined a tetradic schema to describe the growth of theories and, via generalization, also the emergence of new behaviors and living organisms: (1) problem, (2) tentative theory, (3) (attempted) error-elimination (especially by way of critical discussion), and (4) new problem(s). (See Popper's ''Objective Knowledge'', 1972, revised 1979.)
*John Boyd (military strategist)
John Richard Boyd (January 23, 1927 – March 9, 1997) was a United States Air Force fighter pilot and Pentagon consultant during the second half of the 20th century. His theories have been highly influential in military, business, and litiga ...
made his key concept the decision cycle or OODA loop
The OODA loop is the cycle ''observe–orient–decide–act'', developed by military strategist and United States Air Force Colonel John Boyd. Boyd applied the concept to the combat operations process, often at the operational level during m ...
, consisting of four stages: (1) observation (data intake through the senses), (2) orientation (analysis and synthesis of data), (3) decision, and (4) action. Boyd held that his decision cycle has philosophical generality, though for strategists the point remains that, through swift decisions, one can disrupt an opponent's decision cycle.
*Richard McKeon
Richard McKeon (; April 26, 1900 – March 31, 1985) was an American philosopher and longtime professor at the University of Chicago. His ideas formed the basis for the UN's Universal Declaration of Human Rights.
Life, times, and influences
McKeo ...
outlined four classes (each with four subclasses) of modes of philosophical inquiry: (1) Modes of Being (Being); (2) Modes of Thought (That which is); (3) Modes of Fact (Existence); (4) Modes of Simplicity (Experience)—and, corresponding to them, four classes (each with four subclasses) of philosophical semantics: Principles, Methods, Interpretations, and Selections. (See McKeon's "Philosophic Semantics and Philosophic Inquiry" in ''Freedom and History and Other Essays'', 1989.)
*Jonathan Lowe
Edward Jonathan Lowe (; 24 March 1950 – 5 January 2014), usually cited as E. J. Lowe but known personally as Jonathan Lowe, was a British philosopher and academic. He was Professor of Philosophy at Durham University.
Biography
Lowe was bor ...
(E.J. Lowe) argues in ''The Four-Category Ontology'', 2006, for four categories: ''kinds'' (substantial universals), ''attributes'' (relational universals and property-universals), ''objects'' (substantial particulars), and ''modes'' (relational particulars and property-particulars, also known as " tropes"). (See Lowe's "Recent Advances in Metaphysics," 2001Eprint
*Four opposed camps of the morality and nature of evil:
moral absolutism
Moral absolutism is an ethical view that some (potentially all) actions are intrinsically right or wrong. Stealing, for instance, might be considered to be always immoral, even if done for the well-being of others (e.g., stealing food to feed a ...
, amoralism
Moral nihilism (also known as ethical nihilism) is the meta-ethical view that nothing is morally right or wrong.
Moral nihilism is distinct from moral relativism, which allows for actions to be wrong relative to a particular culture or indivi ...
, moral relativism
Moral relativism or ethical relativism (often reformulated as relativist ethics or relativist morality) is used to describe several philosophical positions concerned with the differences in moral judgments across different peoples and cultures. ...
, and moral universalism.
In technology
resin identification code
The ASTM International Resin Identification Coding System, often abbreviated RIC, is a set of symbols appearing on plastic products that identify the plastic resin out of which the product is made. It was developed in 1988 by the Society of t ...
used in recycling to identify low-density polyethylene
Low-density polyethylene (LDPE) is a thermoplastic made from the monomer ethylene. It was the first grade of polyethylene, produced in 1933 by Imperial Chemical Industries (ICI) using a high pressure process via free radical polymerization. Its ...
.
*Most furniture
Furniture refers to movable objects intended to support various human activities such as seating (e.g., stools, chairs, and sofas), eating (tables), storing items, eating and/or working with an item, and sleeping (e.g., beds and hammocks). Fu ...
has four legs – tables, chairs, etc.
*The four color process
Color printing or colour printing is the reproduction of an image or text in color (as opposed to simpler black and white
or monochrome printing). Any natural scene or color photograph can be optically and physiologically dissected into three ...
(CMYK
The CMYK color model (also known as process color, or four color) is a subtractive color model, based on the CMY color model, used in color printing, and is also used to describe the printing process itself. The abbreviation ''CMYK'' refers ...
) is used for printing
Printing is a process for mass reproducing text and images using a master form or template. The earliest non-paper products involving printing include cylinder seals and objects such as the Cyrus Cylinder and the Cylinders of Nabonidus. The ea ...
.
*Wide use of rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s (with four angles and four sides) because they have effective form and capability for close adjacency to each other (houses, rooms, tables, bricks, sheets of paper, screens, film frames).
*In the Rich Text Format
)
As an example, the following RTF code
would be rendered as follows:
This is some bold text.
Character encoding
A standard RTF file can only consist of 7-bit ASCII characters, but can use escape sequences to encode other characters. Th ...
specification, language code 4 is for the Chinese language
Chinese (, especially when referring to written Chinese) is a group of languages spoken natively by the ethnic Han Chinese majority and many minority ethnic groups in Greater China. About 1.3 billion people (or approximately 16% of the wor ...
. Codes for regional variants of Chinese are congruent to .
*Credit card
A credit card is a payment card issued to users (cardholders) to enable the cardholder to pay a merchant for goods and services based on the cardholder's accrued debt (i.e., promise to the card issuer to pay them for the amounts plus the o ...
machines have four-twelve function keys.
*On most phones, the 4 key is associated with the letters G, H, and I, but on the BlackBerry Pearl, it is the key for D and F.
*On many computer keyboard
A computer keyboard is a peripheral input device modeled after the typewriter keyboard which uses an arrangement of buttons or keys to act as mechanical levers or electronic switches. Replacing early punched cards and paper tape technology ...
s, the "4" key may also be used to type the dollar sign
The dollar sign, also known as peso sign, is a symbol consisting of a capital " S" crossed with one or two vertical strokes ($ or ), used to indicate the unit of various currencies around the world, including most currencies denominated "pes ...
($) if the shift key
The Shift key is a modifier key on a keyboard, used to type capital letters and other alternate "upper" characters. There are typically two shift keys, on the left and right sides of the row below the home row. The Shift key's name originated f ...
is held down.
*It is the number of bit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represente ...
s in a nibble
In computing, a nibble (occasionally nybble, nyble, or nybl to match the spelling of byte) is a four-bit aggregation, or half an octet. It is also known as half-byte or tetrade. In a networking or telecommunication context, the nibble is oft ...
, equivalent to half a byte
The byte is a unit of digital information that most commonly consists of eight bits. Historically, the byte was the number of bits used to encode a single character of text in a computer and for this reason it is the smallest addressable unit ...
*In internet slang
Internet slang (also called Internet shorthand, cyber-slang, netspeak, digispeak or chatspeak) is a non-standard or unofficial form of language used by people on the Internet to communicate to one another. An example of Internet slang is "LOL" m ...
, "4" can replace the word "for" (as "four" and "for" are pronounced similarly). For example, typing "4u" instead of "for you".
*In Leet
Leet (or "1337"), also known as eleet or leetspeak, is a system of modified spellings used primarily on the Internet. It often uses character replacements in ways that play on the similarity of their glyphs via reflection or other resemblance. ...
speak, "4" may be used to replace the letter "A".
*The TCP/IP stack
The Internet protocol suite, commonly known as TCP/IP, is a framework for organizing the set of communication protocols used in the Internet and similar computer networks according to functional criteria. The foundational protocols in the suit ...
consists of four layers.
In transport
internal combustion engines
An internal combustion engine (ICE or IC engine) is a heat engine in which the combustion of a fuel occurs with an oxidizer (usually air) in a combustion chamber that is an integral part of the working fluid flow circuit. In an internal combus ...
are called four-stroke
A four-stroke (also four-cycle) engine is an internal combustion (IC) engine in which the piston completes four separate strokes while turning the crankshaft. A stroke refers to the full travel of the piston along the cylinder, in either directio ...
engines because they complete one thermodynamic cycle in four distinct steps: Intake, compression, power, and exhaust.
*Most vehicle
A vehicle (from la, vehiculum) is a machine that transports people or cargo. Vehicles include wagons, bicycles, motor vehicles (motorcycles, cars, trucks, buses, mobility scooters for disabled people), railed vehicles (trains, trams), wa ...
s, including motor vehicle
A motor vehicle, also known as motorized vehicle or automotive vehicle, is a self-propelled land vehicle, commonly wheeled, that does not operate on Track (rail transport), rails (such as trains or trams) and is used for the transportation of pe ...
s, and particularly cars/automobiles and light commercial vehicle
A commercial vehicle is any type of motor vehicle used for transporting goods or paying passengers.
The United States defines a "commercial motor vehicle" as any self-propelled or towed vehicle used on a public highway in interstate commerce to ...
s have four road wheel
A wheel is a circular component that is intended to rotate on an axle Bearing (mechanical), bearing. The wheel is one of the key components of the wheel and axle which is one of the Simple machine, six simple machines. Wheels, in conjunction wi ...
s.
*" Quattro", meaning four in the Italian language, is used by Audi
Audi AG () is a German automotive manufacturer of luxury vehicles headquartered in Ingolstadt, Bavaria, Germany. As a subsidiary of its parent company, the Volkswagen Group, Audi produces vehicles in nine production facilities worldwide.
Th ...
as a trademark to indicate that all-wheel drive
An all-wheel drive vehicle (AWD vehicle) is one with a powertrain capable of providing power to all its wheels, whether full-time or on-demand.
The most common forms of all-wheel drive are:
;1x1 : All unicycles Reflecting one axle with one w ...
(AWD) technologies are used on Audi-branded cars. The word "Quattro" was initially used by Audi in 1980 in its original 4WD coupé, the Audi Quattro
The Audi Quattro is a road and rally car, produced by the German automobile manufacturer Audi, part of the Volkswagen Group. It was first shown at the 1980 Geneva Motor Show on 3 March. Production continued through 1991.
Background
The wo ...
. Audi also has a privately held subsidiary company called quattro GmbH
Audi Sport GmbH, formerly known as quattro GmbH,Audi-Mediacente ...
.
*List of highways numbered 4
Route 4, or Highway 4, may refer to several highways in the following countries:
International
* AH4, Asian Highway 4
* European route E04
* European route E004
* Cairo – Cape Town Highway
Albania
* SH-4 road in Albania from Durres to Kakav ...
In sports
* In theAustralian Football League
The Australian Football League (AFL) is the only fully professional competition of Australian rules football. Through the AFL Commission, the AFL also serves as the sport's governing body and is responsible for controlling the laws of the gam ...
, the top level of Australian rules football
Australian football, also called Australian rules football or Aussie rules, or more simply football or footy, is a contact sport played between two teams of 18 players on an oval field, often a modified cricket ground. Points are scored by k ...
, each team is allowed 4 "interchanges
Interchange may refer to:
Transport
* Interchange (road), a collection of ramps, exits, and entrances between two or more highways
* Interchange (freight rail), the transfer of freight cars between railroad companies
* Interchange station, a rai ...
" (substitute players), who can be freely substituted at any time, subject to a limit on the total number of substitutions.
*In baseball
Baseball is a bat-and-ball sport played between two teams of nine players each, taking turns batting and fielding. The game occurs over the course of several plays, with each play generally beginning when a player on the fielding tea ...
:
**There are four bases in the game: first base
A first baseman, abbreviated 1B, is the player on a baseball or softball team who fields the area nearest first base, the first of four bases a baserunner must touch in succession to score a run. The first baseman is responsible for the majori ...
, second base, third base
A third baseman, abbreviated 3B, is the player in baseball or softball whose responsibility is to defend the area nearest to third base — the third of four bases a baserunner must touch in succession to score a run. In the scoring system us ...
, and home plate
A baseball field, also called a ball field or baseball diamond, is the field upon which the game of baseball is played. The term can also be used as a metonym for a baseball park. The term sandlot is sometimes used, although this usually refers ...
; to score a run, an offensive player must complete, in the sequence shown, a circuit of those four bases.
** When a batter receives four pitches that the umpire declares to be " balls" in a single at-bat, a base on balls
A base on balls (BB), also known as a walk, occurs in baseball when a batter receives four pitches that the umpire calls '' balls'', and is in turn awarded first base without the possibility of being called out. The base on balls is defined in Se ...
, informally known as a "walk", is awarded, with the batter sent to first base.
**For scoring, number 4 is assigned to the second baseman.
**Four is the most runs that can be scored on any single at bat, whereby all three baserunners and the batter score (the most common being via a grand slam
Grand Slam most often refers to:
* Grand Slam (tennis), one player or pair winning all four major annual tournaments, or the tournaments themselves
Grand Slam or Grand slam may also refer to:
Games and sports
* Grand slam, winning category te ...
).
**The fourth batter in the batting lineup is called the cleanup hitter
In baseball, a cleanup hitter is the fourth hitter in the batting order. The cleanup hitter is traditionally the team's most powerful hitter. His job is to "clean up the bases", i.e., drive in base runners.
Theory
The thinking behind the us ...
.
*In basketball
Basketball is a team sport in which two teams, most commonly of five players each, opposing one another on a rectangular Basketball court, court, compete with the primary objective of #Shooting, shooting a basketball (ball), basketball (appr ...
, the number four is used to designate the power forward
The power forward (PF), also known as the four, is one of the five traditional positions in a regulation basketball game. Traditionally, power forwards have played a role similar to centers. When on offense, they typically play with their ba ...
position, often referred to as "the four spot" or "the four".
*In cricket
Cricket is a bat-and-ball game played between two teams of eleven players on a field at the centre of which is a pitch with a wicket at each end, each comprising two bails balanced on three stumps. The batting side scores runs by striki ...
, a four is a specific type of scoring event, whereby the ball crosses the boundary
Boundary or Boundaries may refer to:
* Border, in political geography
Entertainment
*Boundaries (2016 film), ''Boundaries'' (2016 film), a 2016 Canadian film
*Boundaries (2018 film), ''Boundaries'' (2018 film), a 2018 American-Canadian road trip ...
after touching the ground at least one time, scoring four runs. Taking four wickets in four consecutive balls is typically referred to as a double hat trick (two consecutive, overlapping hat tricks).
*In American Football
American football (referred to simply as football in the United States and Canada), also known as gridiron, is a team sport played by two teams of eleven players on a rectangular field with goalposts at each end. The offense, the team with ...
teams get four downs to reach the line of gain.
*In rowing
Rowing is the act of propelling a human-powered watercraft using the sweeping motions of oars to displace water and generate reactional propulsion. Rowing is functionally similar to paddling, but rowing requires oars to be mechanically atta ...
, a four refers to a boat
A boat is a watercraft of a large range of types and sizes, but generally smaller than a ship, which is distinguished by its larger size, shape, cargo or passenger capacity, or its ability to carry boats.
Small boats are typically found on inl ...
for four rowers, with or without coxswain
The coxswain ( , or ) is the person in charge of a boat, particularly its navigation and steering. The etymology of the word gives a literal meaning of "boat servant" since it comes from ''cock'', referring to the cockboat, a type of ship's boat ...
. In rowing nomenclature, 4− represents a coxless four and 4+ represents a coxed four.
*In rugby league
Rugby league football, commonly known as just rugby league and sometimes football, footy, rugby or league, is a full-contact sport played by two teams of thirteen players on a rectangular field measuring 68 metres (75 yards) wide and 112 ...
:
** A try
Try or TRY may refer to:
Music Albums
* ''Try!'', an album by the John Mayer Trio
* ''Try'' (Bebo Norman album) (2014) Songs
* "Try" (Blue Rodeo song) (1987)
* "Try" (Colbie Caillat song) (2014)
* "Try" (Nelly Furtado song) (2004)
* " Try (Ju ...
is worth 4 points.
** One of the two starting centres wears the jersey number 4. (An exception to this rule is the Super League
The Super League (officially known as the Betfred Super League due to sponsorship from Betfred and legally known as Super League Europe), is the top-level of the British rugby league system. At present the league consists of twelve teams, of wh ...
, which uses static squad numbering.)
*In rugby union
Rugby union, commonly known simply as rugby, is a close-contact team sport that originated at Rugby School in the first half of the 19th century. One of the two codes of rugby football, it is based on running with the ball in hand. In its m ...
:
** One of the two starting locks
Lock(s) may refer to:
Common meanings
*Lock and key, a mechanical device used to secure items of importance
*Lock (water navigation), a device for boats to transit between different levels of water, as in a canal
Arts and entertainment
* ''Lock ...
wears the jersey number 4.
** In the standard bonus points system, a point is awarded in the league standings to a team that scores at least 4 tries in a match, regardless of the match result.
In other fields
four-letter word
The phrase four-letter word refers to a set of English-language words written with four letters which are considered profane, including common popular or slang terms for excretory functions, sexual activity and genitalia, blasphemies, terms ...
" is used to describe many swear words in the English language
English is a West Germanic language of the Indo-European language family, with its earliest forms spoken by the inhabitants of early medieval England. It is named after the Angles, one of the ancient Germanic peoples that migrated to the is ...
.
*Four is the only number whose name in English has the same number of letters as its value.
*Four (, formal writing: , pinyin
Hanyu Pinyin (), often shortened to just pinyin, is the official romanization system for Standard Mandarin Chinese in China, and to some extent, in Singapore and Malaysia. It is often used to teach Mandarin, normally written in Chinese for ...
sì) is considered an unlucky number
Numerology (also known as arithmancy) is the belief in an occult, divine or mystical relationship between a number and one or more coinciding events. It is also the study of the numerical value, via an alphanumeric system, of the letters in ...
in Chinese
Chinese can refer to:
* Something related to China
* Chinese people, people of Chinese nationality, citizenship, and/or ethnicity
**''Zhonghua minzu'', the supra-ethnic concept of the Chinese nation
** List of ethnic groups in China, people of ...
, Korean
Korean may refer to:
People and culture
* Koreans, ethnic group originating in the Korean Peninsula
* Korean cuisine
* Korean culture
* Korean language
**Korean alphabet, known as Hangul or Chosŏn'gŭl
**Korean dialects and the Jeju language
** ...
, Vietnamese
Vietnamese may refer to:
* Something of, from, or related to Vietnam, a country in Southeast Asia
** A citizen of Vietnam. See Demographics of Vietnam.
* Vietnamese people, or Kinh people, a Southeast Asian ethnic group native to Vietnam
** Overse ...
and Japanese
Japanese may refer to:
* Something from or related to Japan, an island country in East Asia
* Japanese language, spoken mainly in Japan
* Japanese people, the ethnic group that identifies with Japan through ancestry or culture
** Japanese diaspor ...
cultures mostly in Eastern Asia because it sounds like the word "death" (, pinyin
Hanyu Pinyin (), often shortened to just pinyin, is the official romanization system for Standard Mandarin Chinese in China, and to some extent, in Singapore and Malaysia. It is often used to teach Mandarin, normally written in Chinese for ...
sǐ). To avoid complaints from people with tetraphobia, many numbered product lines skip the "four": e.g. Nokia
Nokia Corporation (natively Nokia Oyj, referred to as Nokia) is a Finnish multinational corporation, multinational telecommunications industry, telecommunications, technology company, information technology, and consumer electronics corporatio ...
cell phones
A mobile phone, cellular phone, cell phone, cellphone, handphone, hand phone or pocket phone, sometimes shortened to simply mobile, cell, or just phone, is a portable telephone that can make and receive calls over a radio frequency link whil ...
(there was no series beginning with a 4 until the Nokia 4.2 The Nokia 4.2 is a Nokia-branded entry-level smartphone developed by HMD Global, running the Android operating system, which was released on 14 May 2019.
Overview
It features 5.71" 19:9 720x1520 pixels IPS LCD display, an octa-core Qualcomm Sn ...
), Palm
Palm most commonly refers to:
* Palm of the hand, the central region of the front of the hand
* Palm plants, of family Arecaceae
**List of Arecaceae genera
* Several other plants known as "palm"
Palm or Palms may also refer to:
Music
* Palm (ba ...
PDAs, etc. Some buildings skip floor 4 or replace the number with the letter "F", particularly in heavily Asian areas. ''See tetraphobia
Tetraphobia () is the practice of avoiding instances of the digit . It is a superstition most common in East Asian nations.
__TOC__
Rationale
The Chinese word for "four" (, pinyin: sì, jyutping: sei3), sounds quite similar to the word for "de ...
'' and ''Numbers in Chinese culture
Some numbers are believed by some to be auspicious or lucky (吉利, ) or inauspicious or unlucky (不吉, ) based on the Chinese word that the number sounds similar to. The numbers 3, 6, and 8 are generally considered to be lucky, while 4 is c ...
''.
*In Pythagorean numerology
Numerology (also known as arithmancy) is the belief in an occult, divine or mystical relationship between a number and one or more coinciding events. It is also the study of the numerical value, via an alphanumeric system, of the letters in ...
(a pseudocience
Pseudoscience consists of statements, beliefs, or practices that claim to be both scientific and factual but are incompatible with the scientific method. Pseudoscience is often characterized by contradictory, exaggerated or unfalsifiable claim ...
) the number 4 represents security and stability.
*The number of characters in a canonical four-character idiom.
*In the NATO phonetic alphabet
The (International) Radiotelephony Spelling Alphabet, commonly known as the NATO phonetic alphabet, is the most widely used set of clear code words for communicating the letters of the Roman alphabet, technically a ''radiotelephonic spellin ...
, the digit 4 is called "fower".
*In astrology
Astrology is a range of Divination, divinatory practices, recognized as pseudoscientific since the 18th century, that claim to discern information about human affairs and terrestrial events by studying the apparent positions of Celestial o ...
, Cancer
Cancer is a group of diseases involving abnormal cell growth with the potential to invade or spread to other parts of the body. These contrast with benign tumors, which do not spread. Possible signs and symptoms include a lump, abnormal b ...
is the 4th astrological sign
In Western astrology, astrological signs are the twelve 30-degree sectors that make up Earth's 360-degree orbit around the Sun. The signs enumerate from the first day of spring, known as the First Point of Aries, which is the vernal equinox. ...
of the Zodiac
The zodiac is a belt-shaped region of the sky that extends approximately 8° north or south (as measured in celestial latitude) of the ecliptic, the Sun path, apparent path of the Sun across the celestial sphere over the course of the year. ...
.
*In Tarot
The tarot (, first known as '' trionfi'' and later as ''tarocchi'' or ''tarocks'') is a pack of playing cards, used from at least the mid-15th century in various parts of Europe to play card games such as Tarocchini. From their Italian roots, ...
, The Emperor is the fourth trump
Trump most commonly refers to:
* Donald Trump (born 1946), 45th president of the United States (2017–2021)
* Trump (card games), any playing card given an ad-hoc high rank
Trump may also refer to:
Businesses and organizations
* Donald J. T ...
or Major Arcana
The Major Arcana are the named or numbered cards in a cartomantic tarot pack, the name being originally given by occultists to the trump cards of a normal tarot pack used for playing card games. There are usually 22 such cards in a standard 78-car ...
card.
*In ''Tetris
''Tetris'' (russian: link=no, Тетрис) is a puzzle video game created by Soviet software engineer Alexey Pajitnov in 1984. It has been published by several companies for multiple platforms, most prominently during a dispute over the approp ...
'', a game named for the Greek word for 4, every shape in the game is formed of 4 blocks each.
*4 represents the number of Justices on the Supreme Court of the United States
The Supreme Court of the United States (SCOTUS) is the highest court in the federal judiciary of the United States. It has ultimate appellate jurisdiction over all U.S. federal court cases, and over state court cases that involve a point o ...
necessary to grant a writ of certiorari
In law, ''certiorari'' is a court process to seek judicial review of a decision of a lower court or government agency. ''Certiorari'' comes from the name of an English prerogative writ, issued by a superior court to direct that the record of ...
(i.e., agree to hear a case; it is one less than the number necessary to render a majority decision) at the court's current size.
*Number Four is a character in the book series ''Lorien Legacies
''Lorien Legacies'' is a series of young adult science fiction books, written by James Frey, Jobie Hughes, and formerly, Greg Boose, under the collective pseudonym Pittacus Lore.
Lorien Legacies
''I am Number Four''
The first book of The ...
.''
*In the performing arts
The performing arts are arts such as music, dance, and drama which are performed for an audience. They are different from the visual arts, which are the use of paint, canvas or various materials to create physical or static art objects. Perform ...
, the fourth wall
The fourth wall is a performance convention in which an invisible, imaginary wall separates actors from the audience. While the audience can see through this ''wall'', the convention assumes the actors act as if they cannot. From the 16th cen ...
is an imaginary barrier which separates the audience from the performers, and is "broken" when performers communicate directly to the audience.
In music
*Inwritten music
Music notation or musical notation is any system used to visually represent wikt:aurally, aurally perceived music played with instrument (music), instruments or singing, sung by the human voice through the use of written, printed, or otherwise ...
, common time
The time signature (also known as meter signature, metre signature, or measure signature) is a notational convention used in Western musical notation to specify how many beats (pulses) are contained in each measure (bar), and which note value ...
is constructed of four beats per measure and a quarter note receives one beat.
*In popular or modern music, the most common time signature
The time signature (also known as meter signature, metre signature, or measure signature) is a notational convention used in Western musical notation to specify how many beats (pulses) are contained in each measure (bar), and which note value ...
is also founded on four beats, i.e., 4/4 having four quarter note
A quarter note (American) or crotchet ( ) (British) is a note (music), musical note played for one quarter of the duration of a whole note (or semibreve). Quarter notes are notated with a filled-in oval note head and a straight, flagless ste ...
beats.
*The common major scale
The major scale (or Ionian mode) is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double i ...
is built on two sets of four notes (e.g., CDEF, GABC), where the first and last notes create an octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
interval (a pair-of-four relationship).
*The interval of a perfect fourth
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to ...
is a foundational element of many genres of music, represented in music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
as the tonic and subdominant
In music, the subdominant is the fourth tonal degree () of the diatonic scale. It is so called because it is the same distance ''below'' the tonic as the dominant is ''above'' the tonicin other words, the tonic is the dominant of the subdomina ...
relationship. Four is also embodied within the circle of fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval ...
(also known as circle of fourths), which reveals the interval of four in more active harmonic contexts.
*The typical number of movements in a symphony
A symphony is an extended musical composition in Western classical music, most often for orchestra. Although the term has had many meanings from its origins in the ancient Greek era, by the late 18th century the word had taken on the meaning com ...
.
*The number of completed, numbered symphonies by Johannes Brahms
Johannes Brahms (; 7 May 1833 – 3 April 1897) was a German composer, pianist, and conductor of the mid- Romantic period. Born in Hamburg into a Lutheran family, he spent much of his professional life in Vienna. He is sometimes grouped wit ...
.
*The number of strings on a violin
The violin, sometimes known as a ''fiddle'', is a wooden chordophone (string instrument) in the violin family. Most violins have a hollow wooden body. It is the smallest and thus highest-pitched instrument (soprano) in the family in regular ...
, a viola
The viola ( , also , ) is a string instrument that is bow (music), bowed, plucked, or played with varying techniques. Slightly larger than a violin, it has a lower and deeper sound. Since the 18th century, it has been the middle or alto voice of ...
, a cello
The cello ( ; plural ''celli'' or ''cellos'') or violoncello ( ; ) is a Bow (music), bowed (sometimes pizzicato, plucked and occasionally col legno, hit) string instrument of the violin family. Its four strings are usually intonation (music), t ...
, double bass
The double bass (), also known simply as the bass () (or #Terminology, by other names), is the largest and lowest-pitched Bow (music), bowed (or plucked) string instrument in the modern orchestra, symphony orchestra (excluding unorthodox addit ...
, a cuatro
Cuatro is Spanish (and other Romance languages) for the number four.
Cuatro may also refer to:
* Cuatro (instrument), name for two distinct Latin American instruments, one from Puerto Rico (see Cuatro) and the other from Venezuela (see Cuatro) ...
, a typical bass guitar
The bass guitar, electric bass or simply bass (), is the lowest-pitched member of the string family. It is a plucked string instrument similar in appearance and construction to an electric or an acoustic guitar, but with a longer neck and ...
, and a ukulele
The ukulele ( ; from haw, ukulele , approximately ), also called Uke, is a member of the lute family of instruments of Portuguese origin and popularized in Hawaii. It generally employs four nylon strings.
The tone and volume of the instrumen ...
, and the number of string pairs on a mandolin
A mandolin ( it, mandolino ; literally "small mandola") is a stringed musical instrument in the lute family and is generally plucked with a pick. It most commonly has four courses of doubled strings tuned in unison, thus giving a total of 8 ...
.
*"Four calling birds" is the gift on the fourth day of Christmas in the carol "The Twelve Days of Christmas
The Twelve Days of Christmas, also known as Twelvetide, is a festive Christian season celebrating the Nativity of Jesus. In some Western ecclesiastical traditions, "Christmas Day" is considered the "First Day of Christmas" and the Twelve Days a ...
".
Groups of four
*Big Four (disambiguation) Big Four or Big 4 may refer to:
Groups of companies
* Big Four accounting firms: Deloitte, Ernst & Young, KPMG, PwC
* Big Four (airlines) in the U.S. in the 20th century: American, Eastern, TWA, United
* Big Four (banking), several grouping ...
*Four basic operations of arithmetic: addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
, subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
, multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
, division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
.
* Greek classical elements (fire
Fire is the rapid oxidation of a material (the fuel) in the exothermic chemical process of combustion, releasing heat, light, and various reaction Product (chemistry), products.
At a certain point in the combustion reaction, called the ignition ...
, air
The atmosphere of Earth is the layer of gases, known collectively as air, retained by Earth's gravity that surrounds the planet and forms its planetary atmosphere. The atmosphere of Earth protects life on Earth by creating pressure allowing f ...
, water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as a ...
, earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
).
* Four seasons: spring
Spring(s) may refer to:
Common uses
* Spring (season)
Spring, also known as springtime, is one of the four temperate seasons, succeeding winter and preceding summer. There are various technical definitions of spring, but local usage of ...
, summer
Summer is the hottest of the four temperate seasons, occurring after spring and before autumn. At or centred on the summer solstice, the earliest sunrise and latest sunset occurs, daylight hours are longest and dark hours are shortest, wit ...
, autumn
Autumn, also known as fall in American English and Canadian English, is one of the four temperate seasons on Earth. Outside the tropics, autumn marks the transition from summer to winter, in September ( Northern Hemisphere) or March ( Sou ...
, winter
Winter is the coldest season of the year in polar and temperate climates. It occurs after autumn and before spring. The tilt of Earth's axis causes seasons; winter occurs when a hemisphere is oriented away from the Sun. Different cultures ...
.
*The Four Seasons (disambiguation)
The Four Seasons, originally referring to the traditional seasons of spring, summer, autumn and winter (typical of a temperate climate), may refer to:
Music
* ''The Four Seasons'' (Vivaldi), a 1725 set of four violin concertos by Antonio Vival ...
*A leap year
A leap year (also known as an intercalary year or bissextile year) is a calendar year that contains an additional day (or, in the case of a lunisolar calendar, a month) added to keep the calendar year synchronized with the astronomical year or s ...
generally occurs every four years.
*Approximately four weeks (4 times 7 days) to a lunar month (synodic month
In lunar calendars, a lunar month is the time between two successive syzygies of the same type: new moons or full moons. The precise definition varies, especially for the beginning of the month.
Variations
In Shona, Middle Eastern, and Europ ...
= 29.53 days). Thus the number four is universally an integral part of primitive sacred calendars.
*Four weeks of Advent
Advent is a Christian season of preparation for the Nativity of Christ at Christmas. It is the beginning of the liturgical year in Western Christianity.
The name was adopted from Latin "coming; arrival", translating Greek ''parousia''.
In ...
(and four Advent candle
An Advent candle is a candle marked with the days of December up to Christmas Eve. It is typically used in a household rather than a church setting: each day in December the candle is burnt down a little more, to the mark for the day, to show t ...
s on the Advent wreath
The Advent wreath, or Advent crown, is a Christian tradition that symbolizes the passage of the four weeks of Advent in the liturgical calendar of the Western church. It is traditionally a Lutheran practice, although it has spread to many othe ...
).
*Four cardinal directions
The four cardinal directions, or cardinal points, are the four main compass directions: north, east, south, and west, commonly denoted by their initials N, E, S, and W respectively. Relative to north, the directions east, south, and west are a ...
: north
North is one of the four compass points or cardinal directions. It is the opposite of south and is perpendicular to east and west. ''North'' is a noun, adjective, or adverb indicating Direction (geometry), direction or geography.
Etymology
T ...
, south
South is one of the cardinal directions or Points of the compass, compass points. The direction is the opposite of north and is perpendicular to both east and west.
Etymology
The word ''south'' comes from Old English ''sūþ'', from earlier Pro ...
, east
East or Orient is one of the four cardinal directions or points of the compass. It is the opposite direction from west and is the direction from which the Sun rises on the Earth.
Etymology
As in other languages, the word is formed from the fa ...
, west
West or Occident is one of the four cardinal directions or points of the compass. It is the opposite direction from east and is the direction in which the Sunset, Sun sets on the Earth.
Etymology
The word "west" is a Germanic languages, German ...
.
*Four Temperaments
The four temperament theory is a proto-psychological theory which suggests that there are four fundamental personality types: sanguine, choleric, melancholic, and phlegmatic. Most formulations include the possibility of mixtures among the types w ...
: sanguine
Sanguine () or red chalk is chalk of a reddish-brown colour, so called because it resembles the colour of dried blood. It has been popular for centuries for drawing (where white chalk only works on coloured paper). The word comes via French fr ...
, choleric
The four temperament theory is a proto-psychological theory which suggests that there are four fundamental personality types: sanguine, choleric, melancholic, and phlegmatic. Most formulations include the possibility of mixtures among the types w ...
, melancholic
Melancholia or melancholy (from el, µέλαινα χολή ',Burton, Bk. I, p. 147 meaning black bile) is a concept found throughout ancient, medieval and premodern medicine in Europe that describes a condition characterized by markedly d ...
, phlegmatic
The four temperament theory is a proto-psychological theory which suggests that there are four fundamental personality types: sanguine, choleric, melancholic, and phlegmatic. Most formulations include the possibility of mixtures among the types w ...
.
*Four Humors
Humorism, the humoral theory, or humoralism, was a system of medicine detailing a supposed makeup and workings of the human body, adopted by Ancient Greek and Roman physicians and philosophers.
Humorism began to fall out of favor in the 1850s ...
: blood
Blood is a body fluid in the circulatory system of humans and other vertebrates that delivers necessary substances such as nutrients and oxygen to the cells, and transports metabolic waste products away from those same cells. Blood in the c ...
, yellow bile
Humorism, the humoral theory, or humoralism, was a system of medicine detailing a supposed makeup and workings of the human body, adopted by Ancient Greek and Roman physicians and philosophers.
Humorism began to fall out of favor in the 1850s ...
, black bile
Melancholia or melancholy (from el, µέλαινα χολή ',Burton, Bk. I, p. 147 meaning black bile) is a concept found throughout ancient, medieval and premodern medicine in Europe that describes a condition characterized by markedly dep ...
, phlegm
Phlegm (; , ''phlégma'', "inflammation", "humour caused by heat") is mucus produced by the respiratory system, excluding that produced by the nasal passages. It often refers to respiratory mucus expelled by coughing, otherwise known as sputum ...
.
*Four Great Ancient Capitals of China
This is a list of historical capitals of China.
Four Great Ancient Capitals
There are traditionally four major historical capitals of China referred to as the "Four Great Ancient Capitals of China" (). The four are Beijing, Nanjing, Luoyang and ...
.
*Four-corner method
The Four-Corner Method () is a character-input method used for encoding Chinese characters into either a computer or a manual typewriter, using four or five numerical digits per character. The Four-Corner Method is also known as the Four-Corner ...
.
*Four Asian Tigers
The Four Asian Tigers (also known as the Four Asian Dragons or Four Little Dragons in Chinese and Korean) are the developed East Asian economies of Hong Kong, Singapore, South Korea, and Taiwan. Between the early 1960s and 1990s, they underwent ra ...
, referring to the economies of Hong Kong
Hong Kong ( (US) or (UK); , ), officially the Hong Kong Special Administrative Region of the People's Republic of China ( abbr. Hong Kong SAR or HKSAR), is a city and special administrative region of China on the eastern Pearl River Delt ...
, Taiwan
Taiwan, officially the Republic of China (ROC), is a country in East Asia, at the junction of the East and South China Seas in the northwestern Pacific Ocean, with the People's Republic of China (PRC) to the northwest, Japan to the nort ...
, South Korea
South Korea, officially the Republic of Korea (ROK), is a country in East Asia, constituting the southern part of the Korea, Korean Peninsula and sharing a Korean Demilitarized Zone, land border with North Korea. Its western border is formed ...
, and Singapore
Singapore (), officially the Republic of Singapore, is a sovereign island country and city-state in maritime Southeast Asia. It lies about one degree of latitude () north of the equator, off the southern tip of the Malay Peninsula, borde ...
* Cardinal principles.
*Four cardinal virtues
The cardinal virtues are four virtues of mind and character in both classical philosophy and Christian theology. They are prudence, justice, fortitude, and temperance. They form a virtue theory of ethics. The term ''cardinal'' comes from the La ...
: justice, prudence, temperance, fortitude.
*Four suits of playing card
A playing card is a piece of specially prepared card stock, heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic that is marked with distinguishing motifs. Often the front (face) and back of each card has a fi ...
s: hearts, diamonds, clubs, spades.
*Four nation
A nation is a community of people formed on the basis of a combination of shared features such as language, history, ethnicity, culture and/or society. A nation is thus the collective identity of a group of people understood as defined by those ...
s of the United Kingdom
The United Kingdom of Great Britain and Northern Ireland, commonly known as the United Kingdom (UK) or Britain, is a country in Europe, off the north-western coast of the continental mainland. It comprises England, Scotland, Wales and North ...
: England, Wales
Wales ( cy, Cymru ) is a Countries of the United Kingdom, country that is part of the United Kingdom. It is bordered by England to the Wales–England border, east, the Irish Sea to the north and west, the Celtic Sea to the south west and the ...
, Scotland
Scotland (, ) is a country that is part of the United Kingdom. Covering the northern third of the island of Great Britain, mainland Scotland has a border with England to the southeast and is otherwise surrounded by the Atlantic Ocean to the ...
, Northern Ireland
Northern Ireland ( ga, Tuaisceart Éireann ; sco, label= Ulster-Scots, Norlin Airlann) is a part of the United Kingdom, situated in the north-east of the island of Ireland, that is variously described as a country, province or region. Nort ...
.
*Four provinces of Ireland
There have been four Provinces of Ireland: Connacht (Connaught), Leinster, Munster, and Ulster. The Irish language, Irish word for this territorial division, , meaning "fifth part", suggests that there were once five, and at times Kingdom_of_ ...
: Munster
Munster ( gle, an Mhumhain or ) is one of the provinces of Ireland, in the south of Ireland. In early Ireland, the Kingdom of Munster was one of the kingdoms of Gaelic Ireland ruled by a "king of over-kings" ( ga, rí ruirech). Following the ...
, Ulster
Ulster (; ga, Ulaidh or ''Cúige Uladh'' ; sco, label= Ulster Scots, Ulstèr or ''Ulster'') is one of the four traditional Irish provinces. It is made up of nine counties: six of these constitute Northern Ireland (a part of the United King ...
, Leinster
Leinster ( ; ga, Laighin or ) is one of the provinces of Ireland, situated in the southeast and east of Ireland. The province comprises the ancient Kingdoms of Meath, Leinster and Osraige. Following the 12th-century Norman invasion of Ir ...
, Connacht
Connacht ( ; ga, Connachta or ), is one of the provinces of Ireland, in the west of Ireland. Until the ninth century it consisted of several independent major Gaelic kingdoms (Uí Fiachrach, Uí Briúin, Uí Maine, Conmhaícne, and Delbhn ...
.
*Four estates: politics
Politics (from , ) is the set of activities that are associated with making decisions in groups, or other forms of power relations among individuals, such as the distribution of resources or status. The branch of social science that studies ...
, administration
Administration may refer to:
Management of organizations
* Management, the act of directing people towards accomplishing a goal
** Administrative assistant, Administrative Assistant, traditionally known as a Secretary, or also known as an admini ...
, judiciary
The judiciary (also known as the judicial system, judicature, judicial branch, judiciative branch, and court or judiciary system) is the system of courts that adjudicates legal disputes/disagreements and interprets, defends, and applies the law ...
, journalism
Journalism is the production and distribution of reports on the interaction of events, facts, ideas, and people that are the "news of the day" and that informs society to at least some degree. The word, a noun, applies to the occupation (profes ...
. Especially in the expression " Fourth Estate", which means journalism.
*Four Corners
The Four Corners is a region of the Southwestern United States consisting of the southwestern corner of Colorado, southeastern corner of Utah, northeastern corner of Arizona, and northwestern corner of New Mexico. The Four Corners area ...
is the only location in the United States where four states come together at a single point: Colorado
Colorado (, other variants) is a state in the Mountain West subregion of the Western United States. It encompasses most of the Southern Rocky Mountains, as well as the northeastern portion of the Colorado Plateau and the western edge of t ...
, Utah
Utah ( , ) is a state in the Mountain West subregion of the Western United States. Utah is a landlocked U.S. state bordered to its east by Colorado, to its northeast by Wyoming, to its north by Idaho, to its south by Arizona, and to it ...
, New Mexico
)
, population_demonym = New Mexican ( es, Neomexicano, Neomejicano, Nuevo Mexicano)
, seat = Santa Fe
, LargestCity = Albuquerque
, LargestMetro = Tiguex
, OfficialLang = None
, Languages = English, Spanish ( New Mexican), Navajo, Ker ...
, and Arizona
Arizona ( ; nv, Hoozdo Hahoodzo ; ood, Alĭ ṣonak ) is a state in the Southwestern United States. It is the 6th largest and the 14th most populous of the 50 states. Its capital and largest city is Phoenix. Arizona is part of the Fou ...
.
* Four Evangelists – Matthew
Matthew may refer to:
* Matthew (given name)
* Matthew (surname)
* ''Matthew'' (ship), the replica of the ship sailed by John Cabot in 1497
* ''Matthew'' (album), a 2000 album by rapper Kool Keith
* Matthew (elm cultivar), a cultivar of the Ch ...
, Mark
Mark may refer to:
Currency
* Bosnia and Herzegovina convertible mark, the currency of Bosnia and Herzegovina
* East German mark, the currency of the German Democratic Republic
* Estonian mark, the currency of Estonia between 1918 and 1927
* F ...
, Luke
People
*Luke (given name), a masculine given name (including a list of people and characters with the name)
*Luke (surname) (including a list of people and characters with the name)
*Luke the Evangelist, author of the Gospel of Luke. Also known as ...
, and John
John is a common English name and surname:
* John (given name)
* John (surname)
John may also refer to:
New Testament
Works
* Gospel of John, a title often shortened to John
* First Epistle of John, often shortened to 1 John
* Secon ...
* Four Doctors of Western Church – Saint Gregory the Great
Pope Gregory I ( la, Gregorius I; – 12 March 604), commonly known as Saint Gregory the Great, was the bishop of Rome from 3 September 590 to his death. He is known for instigating the first recorded large-scale mission from Rome, the Gregori ...
, Saint Ambrose
Ambrose of Milan ( la, Aurelius Ambrosius; ), venerated as Saint Ambrose, ; lmo, Sant Ambroeus . was a theologian and statesman who served as Bishop of Milan from 374 to 397. He expressed himself prominently as a public figure, fiercely promo ...
, Saint Augustine
Augustine of Hippo ( , ; la, Aurelius Augustinus Hipponensis; 13 November 354 – 28 August 430), also known as Saint Augustine, was a theologian and philosopher of Berbers, Berber origin and the bishop of Hippo Regius in Numidia (Roman pr ...
, and Saint Jerome
Jerome (; la, Eusebius Sophronius Hieronymus; grc-gre, Εὐσέβιος Σωφρόνιος Ἱερώνυμος; – 30 September 420), also known as Jerome of Stridon, was a Christian presbyter, priest, Confessor of the Faith, confessor, th ...
* Four Doctors of Eastern Church – Saint John Chrysostom
John Chrysostom (; gr, Ἰωάννης ὁ Χρυσόστομος; 14 September 407) was an important Early Church Father who served as archbishop of Constantinople. He is known for his preaching and public speaking, his denunciation of abu ...
, Saint Basil the Great
Basil of Caesarea, also called Saint Basil the Great ( grc, Ἅγιος Βασίλειος ὁ Μέγας, ''Hágios Basíleios ho Mégas''; cop, Ⲡⲓⲁⲅⲓⲟⲥ Ⲃⲁⲥⲓⲗⲓⲟⲥ; 330 – January 1 or 2, 379), was a bishop of Cae ...
, and Gregory of Nazianzus
Gregory of Nazianzus ( el, Γρηγόριος ὁ Ναζιανζηνός, ''Grēgorios ho Nazianzēnos''; ''Liturgy of the Hours'' Volume I, Proper of Saints, 2 January. – 25 January 390,), also known as Gregory the Theologian or Gregory N ...
and Saint Athanasius
Athanasius I of Alexandria, ; cop, ⲡⲓⲁⲅⲓⲟⲥ ⲁⲑⲁⲛⲁⲥⲓⲟⲩ ⲡⲓⲁⲡⲟⲥⲧⲟⲗⲓⲕⲟⲥ or Ⲡⲁⲡⲁ ⲁⲑⲁⲛⲁⲥⲓⲟⲩ ⲁ̅; (c. 296–298 – 2 May 373), also called Athanasius the Great, ...
* Four Galilean moons
The Galilean moons (), or Galilean satellites, are the four largest moons of Jupiter: Io, Europa, Ganymede, and Callisto. They were first seen by Galileo Galilei in December 1609 or January 1610, and recognized by him as satellites of Jupiter ...
of Jupiter – Io, Europa
Europa may refer to:
Places
* Europe
* Europa (Roman province), a province within the Diocese of Thrace
* Europa (Seville Metro), Seville, Spain; a station on the Seville Metro
* Europa City, Paris, France; a planned development
* Europa Cliff ...
, Ganymede, and Callisto Callisto most commonly refers to:
*Callisto (mythology), a nymph
*Callisto (moon), a moon of Jupiter
Callisto may also refer to:
Art and entertainment
*''Callisto series'', a sequence of novels by Lin Carter
*''Callisto'', a novel by Torsten Kro ...
* The Gang of Four was a Chinese communist
The Chinese Communist Party (CCP), officially the Communist Party of China (CPC), is the founding and sole ruling party of the People's Republic of China (PRC). Under the leadership of Mao Zedong, the CCP emerged victorious in the Chinese Civil ...
political faction.
* The Fantastic Four
The Fantastic Four is a superhero team appearing in American comic books published by Marvel Comics. The team debuted in ''The Fantastic Four'' #1 ( cover dated Nov. 1961), helping usher in a new level of realism in the medium. It was the first ...
: Mr. Fantastic, The Invisible Woman, The Human Torch, The Thing.
* The Teenage Mutant Ninja Turtles
''Teenage Mutant Ninja Turtles'' is an American media franchise created by the comic book artists Kevin Eastman and Peter Laird. It follows Leonardo (Teenage Mutant Ninja Turtles), Leonardo, Michelangelo (Teenage Mutant Ninja Turtles), Miche ...
: Leonardo, Michelangelo, Donatello, Raphael
* The Beatles
The Beatles were an English Rock music, rock band, formed in Liverpool in 1960, that comprised John Lennon, Paul McCartney, George Harrison and Ringo Starr. They are regarded as the Cultural impact of the Beatles, most influential band of al ...
were also known as the "Fab Four": John Lennon, Paul McCartney, George Harrison, Ringo Starr.
* Gang of Four is a British post-punk
Post-punk (originally called new musick) is a broad genre of punk music that emerged in the late 1970s as musicians departed from punk's traditional elements and raw simplicity, instead adopting a variety of avant-garde sensibilities and non-roc ...
rock
Rock most often refers to:
* Rock (geology), a naturally occurring solid aggregate of minerals or mineraloids
* Rock music, a genre of popular music
Rock or Rocks may also refer to:
Places United Kingdom
* Rock, Caerphilly, a location in Wales ...
band formed in the late 1970s.
* Four rivers in the Garden of Eden (Book of Genesis, Genesis 2:10–14): Pishon (perhaps the Jaxartes or Syr Darya), Gihon (perhaps the Oxus or Amu Darya), Hiddekel (Tigris), and P'rat (Euphrates).
* There are also four years in a single Olympiad (duration between the Olympic Games). Many major international sports competitions follow this cycle, among them the FIFA World Cup and its FIFA Women's World Cup, women's version, the FIBA World Championships for FIBA World Championship, men and FIBA World Championship for Women, women, and the Rugby World Cup.
* There are four limbs on the human body.
* Four Houses of Hogwarts in the Harry Potter series: Gryffindor, Hufflepuff, Ravenclaw, Slytherin.
* Four known continents of the world in the ''A Song of Ice and Fire'' series: Westeros, Essos, Sothoryos, Ulthos.
* Each Grand Prix in Nintendo's ''Mario Kart'' series is divided into four cups and each cup is divided into four courses. The Mushroom Cup, Flower Cup, Star Cup, and Special Cup make up the Nitro Grand Prix, while the Shell Cup, Banana Cup, Leaf Cup, and the Lightning Cup make up the Retro Grand Prix.
See also
*List of highways numbered 4
Route 4, or Highway 4, may refer to several highways in the following countries:
International
* AH4, Asian Highway 4
* European route E04
* European route E004
* Cairo – Cape Town Highway
Albania
* SH-4 road in Albania from Durres to Kakav ...
References
*Wells, D. ''The Penguin Dictionary of Curious and Interesting Numbers'' London: Penguin Group. (1987): 55–58External links
Marijn.Org on Why is everything four?
by Penelope Merritt at samuel-beckett.net
The Number 4
{{Authority control Integers 4 (number),