|
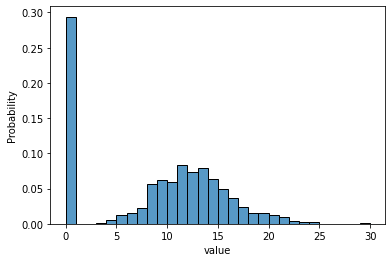
Zero-inflated Model
In statistics, a zero-inflated model is a statistical model based on a zero-inflated probability distribution, i.e. a distribution that allows for frequent zero-valued observations. Zero-inflated Poisson One well-known zero-inflated model is Diane Lambert's zero-inflated Poisson model, which concerns a random event containing excess zero-count data in unit time. For example, the number of insurance claims within a population for a certain type of risk would be zero-inflated by those people who have not taken out insurance against the risk and thus are unable to claim. The zero-inflated Poisson (ZIP) model mixes two zero generating processes. The first process generates zeros. The second process is governed by a Poisson distribution that generates counts, some of which may be zero. The mixture distribution is described as follows: : \Pr (Y = 0) = \pi + (1 - \pi) e^ :\Pr (Y = y_i) = (1 - \pi) \frac ,\qquad y_i = 1,2,3,... where the outcome variable y_i has any non-negative in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Generating Function
In probability theory, the probability generating function of a discrete random variable is a power series representation (the generating function) of the probability mass function of the random variable. Probability generating functions are often employed for their succinct description of the sequence of probabilities Pr(''X'' = ''i'') in the probability mass function for a random variable ''X'', and to make available the well-developed theory of power series with non-negative coefficients. Definition Univariate case If ''X'' is a discrete random variable taking values in the non-negative integers , then the ''probability generating function'' of ''X'' is defined as http://www.am.qub.ac.uk/users/g.gribakin/sor/Chap3.pdf :G(z) = \operatorname (z^X) = \sum_^p(x)z^x, where ''p'' is the probability mass function of ''X''. Note that the subscripted notations ''G''''X'' and ''pX'' are often used to emphasize that these pertain to a particular random variable ''X'', and to its distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Models
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quantity ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurdle Model
A hurdle model is a class of statistical models where a random variable is modelled using two parts, the first which is the probability of attaining value 0, and the second part models the probability of the non-zero values. The use of hurdle models are often motivated by an excess of zeroes in the data, that is not sufficiently accounted for in more standard statistical models. In a hurdle model, a random variable ''x'' is modelled as : \Pr (x = 0) = \theta : \Pr (x \ne 0) = p_(x) where p_(x) is a truncated probability distribution function, truncated at 0. Hurdle models were introduced by John G. Cragg in 1971, where the non-zero values of ''x'' were modelled using a normal model, and a probit model was used to model the zeros. The probit part of the model was said to model the presence of "hurdles" that must be overcome for the values of x to attain non-zero values, hence the designation ''hurdle model''. Hurdle models were later developed for count data, with Poisson, geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Approximation
Sparse approximation (also known as sparse representation) theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more. Sparse decomposition Noiseless observations Consider a linear system of equations x = D\alpha, where D is an underdetermined m\times p matrix (m < p) and . The matrix (typically assumed to be full-rank) is referred to as the dictionary, and is a signal of interest. The core sparse representation problem is defined as the quest for the sparsest possible representation satisfying . Due to the underdetermined nature of , this linear system admits in general infinitely many possible solutions, and among these we seek the one with the fewe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Poisson Distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution. Definition Suppose that :N\sim\operatorname(\lambda), i.e., ''N'' is a random variable whose distribution is a Poisson distribution with expected value λ, and that :X_1, X_2, X_3, \dots are identically distributed random variables that are mutually independent and also independent of ''N''. Then the probability distribution of the sum of N i.i.d. random variables :Y = \sum_^N X_n is a compound Poisson distribution. In the case ''N'' = 0, then this is a sum of 0 terms, so the value of ''Y'' is 0. Hence the conditional distribution of ''Y'' given that ''N'' = 0 is a degenerate distribution. The compound Poisson distribution is obtained by marginalising the j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-truncated Poisson Distribution
In probability theory, the zero-truncated Poisson (ZTP) distribution is a certain discrete probability distribution whose support is the set of positive integers. This distribution is also known as the conditional Poisson distribution or the positive Poisson distribution. It is the conditional probability distribution of a Poisson-distributed random variable, given that the value of the random variable is not zero. Thus it is impossible for a ZTP random variable to be zero. Consider for example the random variable of the number of items in a shopper's basket at a supermarket checkout line. Presumably a shopper does not stand in line with nothing to buy (i.e., the minimum purchase is 1 item), so this phenomenon may follow a ZTP distribution. Since the ZTP is a truncated distribution with the truncation stipulated as , one can derive the probability mass function from a standard Poisson distribution ) as follows: : g(k;\lambda) = P(X = k \mid X > 0) = \frac = \frac = \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdispersion
In statistics, overdispersion is the presence of greater variability (statistical dispersion) in a data set than would be expected based on a given statistical model. A common task in applied statistics is choosing a parametric model to fit a given set of empirical observations. This necessitates an assessment of the fit of the chosen model. It is usually possible to choose the model parameters in such a way that the theoretical population mean of the model is approximately equal to the sample mean. However, especially for simple models with few parameters, theoretical predictions may not match empirical observations for higher moments. When the observed variance is higher than the variance of a theoretical model, overdispersion has occurred. Conversely, underdispersion means that there was less variation in the data than predicted. Overdispersion is a very common feature in applied data analysis because in practice, populations are frequently heterogeneous (non-uniform) contrary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener–Lévy Theorem
Wiener–Lévy theorem is a theorem in Fourier analysis, which states that a function of an absolutely convergent Fourier series has an absolutely convergent Fourier series under some conditions. The theorem was named after Norbert Wiener and Paul Lévy. Norbert Wiener first proved Wiener's 1/''f'' theorem, see Wiener's theorem. It states that if has absolutely convergent Fourier series and is never zero, then its inverse also has an absolutely convergent Fourier series. Wiener–Levy theorem Paul Levy generalized Wiener's result, showing that Let F(\theta ) = \sum\limits_^\infty c_k e^, \quad\theta \in ,2\pi /math> be an absolutely convergent Fourier series with : \, F\, = \sum\limits_^\infty , c_k, has an absolutely convergent Fourier series. The proof can be found in the Zygmund's classic book ''Trigonometric Series''. Example Let H(\theta )=\ln(\theta ) and F(\theta ) = \sum\limits_^\infty p_k e^,(\sum\limits_^\infty p_k = 1 ) is characteristic function of discr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Poisson Distribution
In probability theory, a compound Poisson distribution is the probability distribution of the sum of a number of independent identically-distributed random variables, where the number of terms to be added is itself a Poisson-distributed variable. The result can be either a continuous or a discrete distribution. Definition Suppose that :N\sim\operatorname(\lambda), i.e., ''N'' is a random variable whose distribution is a Poisson distribution with expected value λ, and that :X_1, X_2, X_3, \dots are identically distributed random variables that are mutually independent and also independent of ''N''. Then the probability distribution of the sum of N i.i.d. random variables :Y = \sum_^N X_n is a compound Poisson distribution. In the case ''N'' = 0, then this is a sum of 0 terms, so the value of ''Y'' is 0. Hence the conditional distribution of ''Y'' given that ''N'' = 0 is a degenerate distribution. The compound Poisson distribution is obtained by marginalising the j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the data-generating process. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. Introduction Informally, a statistical model can be thought of as a statistical assumption (or set of statistical assumptions) with a certain property: that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes (denoted r) occurs. For example, we can define rolling a 6 on a die as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes (r), the number of failures (n - r) are random because the total trials (n) are random. For example, we could use the negative binomial distribution to model the number of days n (random) a certain machine works (specified by r) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |