|
Weakly Contractible
In mathematics, a topological space is said to be weakly contractible if all of its homotopy groups are trivial. Property It follows from Whitehead's Theorem that if a CW-complex is weakly contractible then it is contractible. Example Define S^\infty to be the inductive limit of the spheres S^n, n\ge 1. Then this space is weakly contractible. Since S^\infty is moreover a CW-complex, it is also contractible. See Contractibility of unit sphere in Hilbert space for more. The Long Line Long line or longline may refer to: *'' Long Line'', an album by Peter Wolf * Long line (topology), or Alexandroff line, a topological space *Long line (telecommunications), a transmission line in a long-distance communications network *Longline fi ... is an example of a space which is weakly contractible, but not contractible. This does not contradict Whitehead theorem since the Long Line does not have the homotopy type of a CW-complex. Another prominent example for this phenomenon is the Warsaw c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate. A topological space is the most general type of a mathematical space that allows for the definition of limits, continuity, and connectedness. Common types of topological spaces include Euclidean spaces, metric spaces and manifolds. Although very general, the concept of topological spaces is fundamental, and used in virtually every branch of modern mathematics. The study of topological spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, denoted \pi_1(X), which records information about loops in a space. Intuitively, homotopy groups record information about the basic shape, or ''holes'', of a topological space. To define the ''n''-th homotopy group, the base-point-preserving maps from an ''n''-dimensional sphere (with base point) into a given space (with base point) are collected into equivalence classes, called homotopy classes. Two mappings are homotopic if one can be continuously deformed into the other. These homotopy classes form a group, called the ''n''-th homotopy group, \pi_n(X), of the given space ''X'' with base point. Topological spaces with differing homotopy groups are never equivalent ( homeomorphic), but topological spaces that homeomorphic have the same homotopy groups. The notion of homotopy of paths was introduced by Camille Jordan. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whitehead Theorem
In homotopy theory (a branch of mathematics), the Whitehead theorem states that if a continuous mapping ''f'' between CW complexes ''X'' and ''Y'' induces isomorphisms on all homotopy groups, then ''f'' is a homotopy equivalence. This result was proved by J. H. C. Whitehead in two landmark papers from 1949, and provides a justification for working with the concept of a CW complex that he introduced there. It is a model result of algebraic topology, in which the behavior of certain algebraic invariants (in this case, homotopy groups) determines a topological property of a mapping. Statement In more detail, let ''X'' and ''Y'' be topological spaces. Given a continuous mapping :f\colon X \to Y and a point ''x'' in ''X'', consider for any ''n'' ≥ 1 the induced homomorphism :f_*\colon \pi_n(X,x) \to \pi_n(Y,f(x)), where π''n''(''X'',''x'') denotes the ''n''-th homotopy group of ''X'' with base point ''x''. (For ''n'' = 0, π0(''X'') just means the set of path components o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CW-complex
A CW complex (also called cellular complex or cell complex) is a kind of a topological space that is particularly important in algebraic topology. It was introduced by J. H. C. Whitehead (open access) to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial nature that allows for computation (often with a much smaller complex). The ''C'' stands for "closure-finite", and the ''W'' for "weak" topology. Definition CW complex A CW complex is constructed by taking the union of a sequence of topological spaces\emptyset = X_ \subset X_0 \subset X_1 \subset \cdotssuch that each X_k is obtained from X_ by gluing copies of k-cells (e^k_\alpha)_\alpha, each homeomorphic to D^k, to X_ by continuous gluing maps g^k_\alpha: \partial e^k_\alpha \to X_. The maps are also called attaching maps. Each X_k is called the k-skeleton of the complex. The topology of X = \cup_ X_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contractible
In mathematics, a topological space ''X'' is contractible if the identity map on ''X'' is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point within that space. Properties A contractible space is precisely one with the homotopy type of a point. It follows that all the homotopy groups of a contractible space are trivial. Therefore any space with a nontrivial homotopy group cannot be contractible. Similarly, since singular homology is a homotopy invariant, the reduced homology groups of a contractible space are all trivial. For a topological space ''X'' the following are all equivalent: *''X'' is contractible (i.e. the identity map is null-homotopic). *''X'' is homotopy equivalent to a one-point space. *''X'' deformation retracts onto a point. (However, there exist contractible spaces which do not ''strongly'' deformation retract to a point.) *For any space ''Y'', any two maps ''f'',''g' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inductive Limit
In mathematics, a direct limit is a way to construct a (typically large) object from many (typically smaller) objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms (group homomorphism, ring homomorphism, or in general morphisms in the category) between those smaller objects. The direct limit of the objects A_i, where i ranges over some directed set I, is denoted by \varinjlim A_i . (This is a slight abuse of notation as it suppresses the system of homomorphisms that is crucial for the structure of the limit.) Direct limits are a special case of the concept of colimit in category theory. Direct limits are dual to inverse limits, which are also a special case of limits in category theory. Formal definition We will first give the definition for algebraic structures like groups and modules, and then the general definition, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contractibility Of Unit Sphere In Hilbert Space
In mathematics, Kuiper's theorem (after Nicolaas Kuiper) is a result on the topology of operators on an infinite-dimensional, complex Hilbert space ''H''. It states that the space GL(''H'') of invertible bounded endomorphisms of ''H'' is such that all maps from any finite complex ''Y'' to GL(''H'') are homotopic to a constant, for the norm topology on operators. A significant corollary, also referred to as ''Kuiper's theorem'', is that this group is weakly contractible, ''ie.'' all its homotopy groups are trivial. This result has important uses in topological K-theory. General topology of the general linear group For finite dimensional ''H'', this group would be a complex general linear group and not at all contractible. In fact it is homotopy equivalent to its maximal compact subgroup, the unitary group ''U'' of ''H''. The proof that the complex general linear group and unitary group have the same homotopy type is by the Gram-Schmidt process, or through the matrix polar d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Line (topology)
In topology, the long line (or Alexandroff line) is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties (e.g., it is neither Lindelöf nor separable). Therefore, it serves as one of the basic counterexamples of topology. Intuitively, the usual real-number line consists of a countable number of line segments [0,1) laid end-to-end, whereas the long line is constructed from an uncountable number of such segments. Definition The closed long ray L is defined as the cartesian product of the First uncountable ordinal, first uncountable ordinal \omega_1 with the Interval (mathematics), half-open interval [0, 1), equipped with the order topology that arises from the lexicographical order on \omega_1 \times [0,1). The open long ray is obtained from the closed long ray by removing the smallest element (0, 0). The long line is obtained by putting together a long ray i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
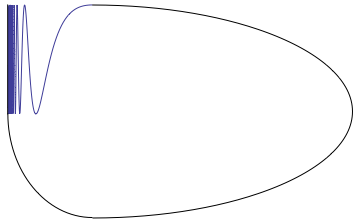
Warsaw Circle
Shape theory is a branch of topology that provides a more global view of the topological spaces than homotopy theory. The two coincide on compacta dominated homotopically by finite polyhedra. Shape theory associates with the Čech homology theory while homotopy theory associates with the singular homology theory. Background Shape theory was reinvented, further developed and promoted by the Polish mathematician Karol Borsuk in 1968. Actually, the name ''shape theory'' was coined by Borsuk. Warsaw Circle Borsuk lived and worked in Warsaw, hence the name of one of the fundamental examples of the area, the Warsaw circle. It is a compact subset of the plane produced by "closing up" a topologist's sine curve with an arc. The homotopy groups of the Warsaw circle are all trivial, just like those of a point, and so any map between the Warsaw circle and a point induces a weak homotopy equivalence. However these two spaces are not homotopy equivalent. So by the Whitehead theorem, the War ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Twist (mathematics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity (mathematics), continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopy, homotopies. A property that is invariant under such deformations is a topological property. Basic exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |