|
Unlink
In the mathematical field of knot theory, an unlink is a link that is equivalent (under ambient isotopy) to finitely many disjoint circles in the plane. Properties * An ''n''-component link ''L'' ⊂ S3 is an unlink if and only if there exists ''n'' disjointly embedded discs ''D''''i'' ⊂ S3 such that ''L'' = ∪''i''∂''D''''i''. * A link with one component is an unlink if and only if it is the unknot. * The link group of an ''n''-component unlink is the free group on ''n'' generators, and is used in classifying Brunnian links. Examples * The Hopf link is a simple example of a link with two components that is not an unlink. * The Borromean rings form a link with three components that is not an unlink; however, any two of the rings considered on their own do form a two-component unlink. * Taizo Kanenobu has shown that for all ''n'' > 1 there exists a hyperbolic link of ''n'' components such that any proper sublink is an unlink ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link Group
In knot theory, an area of mathematics, the link group of a link is an analog of the knot group of a knot. They were described by John Milnor in his Ph.D. thesis, . Notably, the link group is not in general the fundamental group of the link complement. Definition The link group of an ''n''-component link is essentially the set of (''n'' + 1)-component links extending this link, up to link homotopy. In other words, each component of the extended link is allowed to move through regular homotopy (homotopy through immersions), knotting or unknotting itself, but is not allowed to move through other components. This is a weaker condition than isotopy: for example, the Whitehead link has linking number 0, and thus is link homotopic to the unlink, but it is not isotopic to the unlink. The link group is not the fundamental group of the link complement, since the components of the link are allowed to move through themselves, though not each other, but thus is a q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
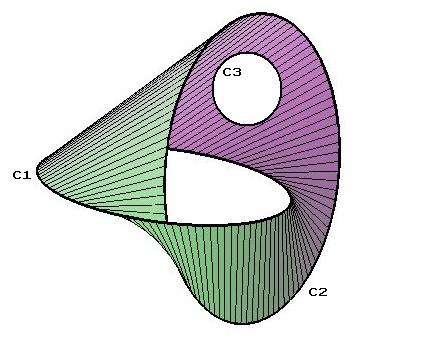
Brunnian Links
In knot theory, a branch of topology, a Brunnian link is a nontrivial link that becomes a set of trivial unlinked circles if any one component is removed. In other words, cutting any loop frees all the other loops (so that no two loops can be directly linked). The name ''Brunnian'' is after Hermann Brunn. Brunn's 1892 article ''Über Verkettung'' included examples of such links. Examples The best-known and simplest possible Brunnian link is the Borromean rings, a link of three unknots. However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: Image:Brunnian-3-not-Borromean.svg, 12-crossing link. Image:Three-triang-18crossings-Brunnian.svg, 18-crossing link. Image:Three-interlaced-squares-Brunnian-24crossings.svg, 24-crossing link. The simplest Brunnian link other than the 6-cros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brunnian Link
In knot theory, a branch of topology, a Brunnian link is a nontrivial link that becomes a set of trivial unlinked circles if any one component is removed. In other words, cutting any loop frees all the other loops (so that no two loops can be directly linked). The name ''Brunnian'' is after Hermann Brunn. Brunn's 1892 article ''Über Verkettung'' included examples of such links. Examples The best-known and simplest possible Brunnian link is the Borromean rings, a link of three unknots. However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: Image:Brunnian-3-not-Borromean.svg, 12-crossing link. Image:Three-triang-18crossings-Brunnian.svg, 18-crossing link. Image:Three-interlaced-squares-Brunnian-24crossings.svg, 24-crossing link. The simplest Brunnian link other than the 6-cros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In the mathematical field of topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, Unknot, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3 (in topology, a circle is not bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of descr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borromean Rings
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing. The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as a coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the logo of Ballantine beer, giving them the alternative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whitehead Link
In knot theory, the Whitehead link, named for J. H. C. Whitehead, is one of the most basic links. It can be drawn as an alternating link with five crossings, from the overlay of a circle and a figure-eight shaped loop. Structure A common way of describing this knot is formed by overlaying a figure-eight shaped loop with another circular loop surrounding the crossing of the figure-eight. The above-below relation between these two unknots is then set as an alternating link, with the consecutive crossings on each loop alternating between under and over. This drawing has five crossings, one of which is the self-crossing of the figure-eight curve, which does not count towards the linking number. Because the remaining crossings have equal numbers of under and over crossings on each loop, its linking number is 0. It is not isotopic to the unlink, but it is link homotopic to the unlink. Although this construction of the knot treats its two loops differently from each other, the two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hopf Link
In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once, and is named after Heinz Hopf. Geometric realization A concrete model consists of two unit circles in perpendicular planes, each passing through the center of the other.. See in particulap. 77 This model minimizes the ropelength of the link and until 2002 the Hopf link was the only link whose ropelength was known. The convex hull of these two circles forms a shape called an oloid. Properties Depending on the relative orientations of the two components the linking number of the Hopf link is ±1. The Hopf link is a (2,2)-torus link with the braid word :\sigma_1^2.\, The knot complement of the Hopf link is R × ''S''1 × ''S''1, the cylinder over a torus. This space has a locally Euclidean geometry, so the Hopf link is not a hyperbolic link. The knot group of the Hopf link (the fund ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambient Isotopy
In the mathematical subject of topology, an ambient isotopy, also called an ''h-isotopy'', is a kind of continuous distortion of an ambient space, for example a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the other without breaking it. Such a distortion is an example of an ambient isotopy. More precisely, let N and M be manifolds and g and h be embeddings of N in M. A continuous map :F:M \times ,1\rightarrow M is defined to be an ambient isotopy taking g to h if F_0 is the identity map, each map F_t is a homeomorphism from M to itself, and F_1 \circ g = h. This implies that the orientation must be preserved by ambient isotopies. For example, two knots that are mirror images of each other are, in general, not equivalent. See also * Isotopy * Regular homotopy *Regular isotopy References *M. A. Armstrong, ''Basic Topology'', Springer-Verlag Springer Science+Business Med ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknot
In the mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a knot tied into it, unknotted. To a knot theorist, an unknot is any embedded topological circle in the 3-sphere that is ambient isotopic (that is, deformable) to a geometrically round circle, the standard unknot. The unknot is the only knot that is the boundary of an embedded disk, which gives the characterization that only unknots have Seifert genus 0. Similarly, the unknot is the identity element with respect to the knot sum operation. Unknotting problem Deciding if a particular knot is the unknot was a major driving force behind knot invariants, since it was thought this approach would possibly give an efficient algorithm to recognize the unknot from some presentation such as a knot diagram. Unknot recognition is known to be in both NP and co-NP. It is known that knot Floer homology and Khova ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



.jpg)

