|
Ungula
In solid geometry, an ungula is a region of a solid of revolution, cut off by a plane oblique to its base. A common instance is the spherical wedge. The term ''ungula'' refers to the hoof of a horse, an anatomical feature that defines a class of mammals called ungulates. The volume of an ungula of a cylinder was calculated by Grégoire de Saint Vincent. Two cylinders with equal radii and perpendicular axes intersect in four double ungulae. Blaise Pascalbr>Lettre de Dettonville a Carcavidescribes the onglet and double onglet, link from HathiTrust The bicylinder formed by the intersection had been measured by Archimedes in The Method of Mechanical Theorems, but the manuscript was lost until 1906. A historian of calculus described the role of the ungula in integral calculus: :Grégoire himself was primarily concerned to illustrate by reference to the ''ungula'' that volumetric integration could be reduced, through the ''ductus in planum'', to a consideration of geometric relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ungulate
Ungulates ( ) are members of the diverse clade Ungulata which primarily consists of large mammals with hooves. These include odd-toed ungulates such as horses, rhinoceroses, and tapirs; and even-toed ungulates such as cattle, pigs, giraffes, camels, sheep, deer, and hippopotamuses. Cetaceans such as whales, dolphins, and porpoises are also classified as even-toed ungulates, although they do not have hooves. Most terrestrial ungulates use the hoofed tips of their toes to support their body weight while standing or moving. The term means, roughly, "being hoofed" or "hoofed animal". As a descriptive term, "ungulate" normally excludes cetaceans as they do not possess most of the typical morphological characteristics of other ungulates, but recent discoveries indicate that they were also descended from early artiodactyls. Ungulates are typically herbivorous and many employ specialized gut bacteria to allow them to digest cellulose. Some modern species, such as pigs, are omnivorous, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Wedge
In geometry, a spherical wedge or ungula is a portion of a ball bounded by two plane semidisks and a spherical lune (termed the wedge's ''base''). The angle between the radii lying within the bounding semidisks is the dihedral . If is a semidisk that forms a ball when completely revolved about the ''z''-axis, revolving only through a given produces a spherical wedge of the same angle . Beman (2008) remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon." A spherical wedge of radians (180°) is called a ''hemisphere'', while a spherical wedge of radians (360°) constitutes a complete ball. The volume of a spherical wedge can be intuitively related to the definition in that while the volume of a ball of radius is given by , the volume a spherical wedge of the same radius is given by :V = \frac \cdot \tfrac43 \pi r^3 = \tfrac23 \alpha r^3\,. Extrapolating the same principle and considering that the surface area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steinmetz Solid
In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse. The intersection of two cylinders is called a bicylinder. Topologically, it is equivalent to a square hosohedron. The intersection of three cylinders is called a tricylinder. A bisected bicylinder is called a vault, and a cloister vault in architecture has this shape. Steinmetz solids are named after mathematician Charles Proteus Steinmetz, who solved the problem of determining the volume of the intersection. However, the same problem had been solved earlier, by Archimedes in the ancient Greek world, Zu Chongzhi in ancient China, and Piero della Francesca in the early Italian Renaissance. Bicylinder A bicylinder generated by two cylinders with radius r has the ;volume :V=\frac r^3 and the ;surface area :A=16 r^2. The upper half of a bicylinder is the square ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mammal
Mammals () are a group of vertebrate animals constituting the class Mammalia (), characterized by the presence of mammary glands which in females produce milk for feeding (nursing) their young, a neocortex (a region of the brain), fur or hair, and three middle ear bones. These characteristics distinguish them from reptiles (including birds) from which they diverged in the Carboniferous, over 300 million years ago. Around 6,400 extant species of mammals have been described divided into 29 orders. The largest orders, in terms of number of species, are the rodents, bats, and Eulipotyphla (hedgehogs, moles, shrews, and others). The next three are the Primates (including humans, apes, monkeys, and others), the Artiodactyla ( cetaceans and even-toed ungulates), and the Carnivora (cats, dogs, seals, and others). In terms of cladistics, which reflects evolutionary history, mammals are the only living members of the Synapsida (synapsids); this clade, together with Saur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Wedge
In geometry, a spherical wedge or ungula is a portion of a ball bounded by two plane semidisks and a spherical lune (termed the wedge's ''base''). The angle between the radii lying within the bounding semidisks is the dihedral . If is a semidisk that forms a ball when completely revolved about the ''z''-axis, revolving only through a given produces a spherical wedge of the same angle . Beman (2008) remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon." A spherical wedge of radians (180°) is called a ''hemisphere'', while a spherical wedge of radians (360°) constitutes a complete ball. The volume of a spherical wedge can be intuitively related to the definition in that while the volume of a ball of radius is given by , the volume a spherical wedge of the same radius is given by :V = \frac \cdot \tfrac43 \pi r^3 = \tfrac23 \alpha r^3\,. Extrapolating the same principle and considering that the surface area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicylinder
In geometry, a Steinmetz solid is the solid body obtained as the intersection of two or three cylinders of equal radius at right angles. Each of the curves of the intersection of two cylinders is an ellipse. The intersection of two cylinders is called a bicylinder. Topologically, it is equivalent to a square hosohedron. The intersection of three cylinders is called a tricylinder. A bisected bicylinder is called a vault, and a cloister vault in architecture has this shape. Steinmetz solids are named after mathematician Charles Proteus Steinmetz, who solved the problem of determining the volume of the intersection. However, the same problem had been solved earlier, by Archimedes in the ancient Greek world, Zu Chongzhi in ancient China, and Piero della Francesca in the early Italian Renaissance. Bicylinder A bicylinder generated by two cylinders with radius r has the ;volume :V=\frac r^3 and the ;surface area :A=16 r^2. The upper half of a bicylinder is the square case of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution'') that lies on the same plane. The surface created by this revolution and which bounds the solid is the surface of revolution. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area ( Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the axis o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Geometry
In mathematics, solid geometry or stereometry is the traditional name for the geometry of Three-dimensional space, three-dimensional, Euclidean spaces (i.e., 3D geometry). Stereometry deals with the measurements of volumes of various solid figures (or 3D figures), including Pyramid (geometry), pyramids, Prism (geometry), prisms and other polyhedrons; Cylinder (geometry), cylinders; cone (geometry), cones; Frustum, truncated cones; and ball (mathematics), balls bounded by spheres. History The Pythagoreanism, Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonism, Platonists. Eudoxus of Cnidus, Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.Paraphrased and taken in part from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margaret Baron
Margaret E. Baron (1915 – 16 August 1996) was a British mathematics educator and historian of mathematics known for her book on the history of calculus. Life Baron was originally from Gateshead, in northeastern England, and earned a bachelor's degree from Durham University through King's College, Newcastle, which later became Newcastle University. She worked for a year as an English teacher in Frankfurt, and in 1938 became a mathematics teacher at the Bede School for Girls, later to become part of Sunderland College. Because she married George Baron, a teacher at the corresponding boys' school, she was dismissed as a teacher in 1940. She took two more teaching posts, at the Royal Grammar School, Newcastle upon Tyne and the High Storrs School in Sheffield, before leaving work to raise her family in Gateshead. Her husband returned from war service in 1946, and they moved to London. Eventually she returned to teaching, at Goldsmiths' College and then, in 1957, as head of mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Google Books
Google Books (previously known as Google Book Search, Google Print, and by its code-name Project Ocean) is a service from Google Inc. that searches the full text of books and magazines that Google has scanned, converted to text using optical character recognition (OCR), and stored in its digital database.The basic Google book link is found at: https://books.google.com/ . The "advanced" interface allowing more specific searches is found at: https://books.google.com/advanced_book_search Books are provided either by publishers and authors through the Google Books Partner Program, or by Google's library partners through the Library Project. Additionally, Google has partnered with a number of magazine publishers to digitize their archives. The Publisher Program was first known as Google Print when it was introduced at the Frankfurt Book Fair in October 2004. The Google Books Library Project, which scans works in the collections of library partners and adds them to the digital invent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
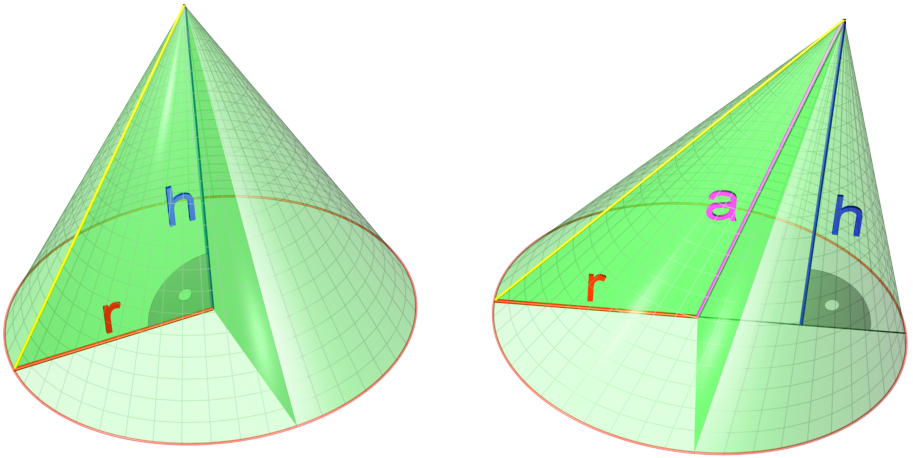
Conical Ungula
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shell Integration
Shell integration (the shell method in integral calculus) is a method for calculating the volume of a solid of revolution, when integrating along an axis ''perpendicular to'' the axis of revolution. This is in contrast to disc integration which integrates along the axis ''parallel'' to the axis of revolution. Definition The shell method goes as follows: Consider a volume in three dimensions obtained by rotating a cross-section in the -plane around the -axis. Suppose the cross-section is defined by the graph of the positive function on the interval . Then the formula for the volume will be: :2 \pi \int_a^b x f(x)\, dx If the function is of the coordinate and the axis of rotation is the -axis then the formula becomes: :2 \pi \int_a^b y f(y)\, dy If the function is rotating around the line then the formula becomes: :\begin \displaystyle 2 \pi \int_a^b (x-h) f(x)\,dx, & \text\ h \le a < b\\ \displaystyle 2 \pi \int_a^b (h-x) f(x)\,dx, & \text\ a < b \le h, \end and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
