 |
Urn Model
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems.Dodge, Yadolah (2003) ''Oxford Dictionary of Statistical Terms'', OUP. History In '' Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the '' inverse probability'' problem, and was a topic o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Election
An election is a formal group decision-making process by which a population chooses an individual or multiple individuals to hold public office. Elections have been the usual mechanism by which modern representative democracy has operated since the 17th century. Elections may fill offices in the legislature, sometimes in the executive and judiciary, and for regional and local government. This process is also used in many other private and business organisations, from clubs to voluntary associations and corporations. The global use of elections as a tool for selecting representatives in modern representative democracies is in contrast with the practice in the democratic archetype, ancient Athens, where the elections were considered an oligarchic institution and most political offices were filled using sortition, also known as allotment, by which officeholders were chosen by lot. Electoral reform describes the process of introducing fair electoral systems wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided dice rolled ''n'' times. For ''n'' independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the prefix, and ''k'' the suffix). The Bernoulli distribution models the outcome of a single Bernoulli tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number ''X'' of Bernoulli trials needed to get one success, supported on the set \; * The probability distribution of the number ''Y'' = ''X'' − 1 of failures before the first success, supported on the set \. Which of these is called the geometric distribution is a matter of convention and convenience. These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of the number ''X''); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires ''k'' independent trials, each with success probability ''p''. If the probability of suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
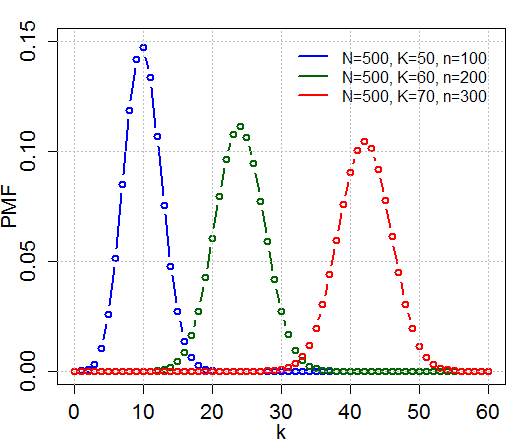 |
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ('' sampling without replacement'' from a finite population). A random variable X follows the hype ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Hoppe Urn
Hoppe or Hoppé is a German surname that may refer to: * Art Hoppe (1925–2000), columnist for the San Francisco Chronicle * Bettina Hoppe (born 21 May 1974), German actress. *Carl Hoppe (1897–1981), painter *David Heinrich Hoppe (1760–1846), German botanist * E. O. Hoppé (1878–1972), German-born British portrait, landscape and travel photographer *Else Hoppe, Czech figure skater *Erik Hoppe (1896–1968), Danish painter *Felicitas Hoppe (born 1960), German writer * Felix Hoppe-Seyler (1825–1895), German physiologist and chemist * Gunnar Hoppe (1914–2005), Swedish Quaternary geologist and geographer * Hans-Hermann Hoppe (born 1949), economics professor *Hans-Joachim Hoppe (born 1945), German expert on Russian and East European affairs *Jenny Hoppe (1870–1934), German-Belgian painter * Johannes Hoppe (born 1907), German astronomer ** 3499 Hoppe, a main-belt asteroid named after Johannes Hoppe *Kelly Hoppe, Canadian musician *Marianne Hoppe (1909–2002), German actress ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters ''n'' and ''p'' is the discrete probability distribution of the number of successes in a sequence of ''n'' independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: ''success'' (with probability ''p'') or ''failure'' (with probability q=1-p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., ''n'' = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size ''n'' drawn with replacement from a population of size ''N''. If the sampling is carried out without replacement, the draws are not independent and so the resultin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pólya Urn Model
In statistics, a Pólya urn model (also known as a Pólya urn scheme or simply as Pólya's urn), named after George Pólya, is a type of statistical model used as an idealized mental exercise framework, unifying many treatments. In an urn model, objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. In the basic Pólya urn model, the urn contains ''x'' white and ''y'' black balls; one ball is drawn randomly from the urn and its color observed; it is then returned in the urn, and an additional ball of the same color is added to the urn, and the selection process is repeated. Questions of interest are the evolution of the urn population and the sequence of colors of the balls drawn out. This endows the urn with a self-reinforcing property sometimes expressed as '' the rich get richer''. Note that in some sense, the Pólya urn model is the "opposite" of the model of sampling without replacement, where every ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Beta-binomial Model
In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of ''n'' trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data. The beta-binomial is a one-dimensional version of the Dirichlet-multinomial distribution as the binomial and beta distributions are univariate versions of the multinomial and Dirichlet distributions respectively. The special case where ''α'' and ''β'' are integers is also known as the negative hypergeometric distribution. Motivation and derivation As a compou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Sortition
In governance, sortition (also known as selection by lottery, selection by lot, allotment, demarchy, stochocracy, aleatoric democracy, democratic lottery, and lottocracy) is the selection of political officials as a random sample from a larger pool of candidates. The system intends to ensure that all competent and interested parties have an equal chance of holding public office. It also minimizes factionalism, since there would be no point making promises to win over key constituencies if one was to be chosen by lot, while elections, by contrast, foster it. In ancient Athenian democracy, sortition was the traditional and primary method for appointing political officials, and its use was regarded as a principal characteristic of democracy. Today, sortition is commonly used to select prospective jurors in common-law systems and is sometimes used in forming citizen groups with political advisory power. History Ancient Athens Athenian democracy developed in the 6th century BC o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |