|
Ultrarelativistic Limit
In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light . The expression for the relativistic energy of a particle with rest mass and momentum is given by :E^2 = m^2 c^4 + p^2 c^2. The energy of an ultrarelativistic particle is almost completely due to its momentum (), and thus can be approximated by . This can result from holding the mass fixed and increasing to very large values (the usual case); or by holding the energy fixed and shrinking the mass to negligible values. The latter is used to derive orbits of massless particles such as the photon from those of massive particles (cf. Kepler problem in general relativity). In general, the ultrarelativistic limit of an expression is the resulting simplified expression when pc \gg mc^2 is assumed. Or, similarly, in the limit where the Lorentz factor \gamma = 1/\sqrt is very large (\gamma \gg 1). Expression including mass value While it is possible to use the approximation E = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rapidity
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with distance and time coordinates. For one-dimensional motion, rapidities are additive whereas velocities must be combined by Einstein's velocity-addition formula. For low speeds, rapidity and velocity are proportional but, for higher velocities, rapidity takes a larger value, with the rapidity of light being infinite. Using the inverse hyperbolic function , the rapidity corresponding to velocity is where ''c'' is the velocity of light. For low speeds, is approximately . Since in relativity any velocity is constrained to the interval the ratio satisfies . The inverse hyperbolic tangent has the unit interval for its domain and the whole real line for its image; that is, the interval maps onto . History In 1908 Hermann Minkowski ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates: # The laws of physics are invariant (that is, identical) in all inertial frames of reference (that is, frames of reference with no acceleration). # The speed of light in vacuum is the same for all observers, regardless of the motion of the light source or the observer. Origins and significance Special relativity was originally proposed by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".Albert Einstein (1905)''Zur Elektrodynamik bewegter Körper'', ''Annalen der Physik'' 17: 891; English translatioOn the Electrodynamics of Moving Bodiesby George Barker Jeffery and Wilfrid Perrett (1923); Another English translation On the Electrodynamics of Moving Bodies by Megh Nad Saha (1920). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical mechanics, if the present state is known, it is possible to predict how it will move in the future (determinism), and how it has moved in the past (reversibility). The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on foundational works of Sir Isaac Newton, and the mathematical methods invented by Gottfried Wilhelm Leibniz, Joseph-Louis Lagrange, Leonhard Euler, and other contemporaries, in the 17th century to describe the motion of bodies under the influence of a system of forces. Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relativistic Particle
A relativistic particle is a particle which moves with a relativistic speed; that is, a speed comparable to the speed of light. This is achieved by photons to the extent that effects described by special relativity are able to describe those of such particles themselves. Several approaches exist as a means of describing the motion of single and multiple relativistic particles, with a prominent example being postulations through Dirac equations of single particle motion. Massive particles are relativistic when their kinetic energy is comparable to or greater than the energy mc^2 corresponding to their rest mass. In other words, a massive particle is relativistic when its total mass-energy (rest mass + kinetic energy) is at least twice its rest mass. This condition implies that the particle's speed is close to the speed of light. According to the Lorentz factor formula, this requires the particle to move at roughly 85% of the speed of light. Such relativistic particles are g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutrinos
A neutrino ( ; denoted by the Greek letter ) is a fermion (an elementary particle with spin of ) that interacts only via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass is so small ('' -ino'') that it was long thought to be zero. The rest mass of the neutrino is much smaller than that of the other known elementary particles excluding massless particles. The weak force has a very short range, the gravitational interaction is extremely weak due to the very small mass of the neutrino, and neutrinos do not participate in the strong interaction. Thus, neutrinos typically pass through normal matter unimpeded and undetected. Weak interactions create neutrinos in one of three leptonic flavors: electron neutrinos muon neutrinos (), or tau neutrinos (), in association with the corresponding charged lepton. Although neutrinos were long believed to be massless, it is now known that there are three discret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Error
The approximation error in a data value is the discrepancy between an exact value and some ''approximation'' to it. This error can be expressed as an absolute error (the numerical amount of the discrepancy) or as a relative error (the absolute error divided by the data value). An approximation error can occur because of computing machine precision or measurement error (e.g. the length of a piece of paper is 4.53 cm but the ruler only allows you to estimate it to the nearest 0.1 cm, so you measure it as 4.5 cm). In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm. Formal definition One commonly distinguishes between the relative error and the absolute error. Given some value ''v'' and its approximation ''v''approx, the absolute error is :\epsilon = , v-v_\text, \ , where the vertical bars denote the absolute value. If v \ne 0, the relative error is : \eta = \frac = \left, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Acceleration
In relativity theory, proper acceleration is the physical acceleration (i.e., measurable acceleration as by an accelerometer) experienced by an object. It is thus acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured. Gravitation therefore does not cause proper acceleration, because the same gravity acts equally on the inertial observer. As a consequence, all inertial observers always have a proper acceleration of zero. Proper acceleration contrasts with coordinate acceleration, which is dependent on choice of coordinate systems and thus upon choice of observers (see three-acceleration in special relativity). In the standard inertial coordinates of special relativity, for unidirectional motion, proper acceleration is the rate of change of proper velocity with respect to coordinate time. In an inertial frame in which the object is momentarily at rest, the proper acceleration 3-vector, combined with a ze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Expansion
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series, when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relativistic Energy
Relativity may refer to: Physics * Galilean relativity, Galileo's conception of relativity * Numerical relativity, a subfield of computational physics that aims to establish numerical solutions to Einstein's field equations in general relativity * Principle of relativity, used in Einstein's theories and derived from Galileo's principle * Theory of relativity, a general treatment that refers to both special relativity and general relativity ** General relativity, Albert Einstein's theory of gravitation ** Special relativity, a theory formulated by Albert Einstein, Henri Poincaré, and Hendrik Lorentz ** '' Relativity: The Special and the General Theory'', a 1920 book by Albert Einstein Social sciences * Linguistic relativity * Cultural relativity * Moral relativity Arts and entertainment Music * Relativity Music Group, a Universal subsidiary record label for releasing film soundtracks * Relativity Records, an American record label * Relativity (band), a Scots-Irish trad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
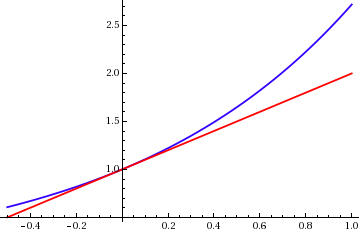
Lorentz Factor
The Lorentz factor or Lorentz term is a quantity expressing how much the measurements of time, length, and other physical properties change for an object while that object is moving. The expression appears in several equations in special relativity, and it arises in derivations of the Lorentz transformations. The name originates from its earlier appearance in Lorentzian electrodynamics – named after the Dutch physicist Hendrik Lorentz. It is generally denoted (the Greek lowercase letter gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as (Greek uppercase-gamma) rather than . Definition The Lorentz factor is defined as :\gamma = \frac = \frac = \frac , where: *''v'' is the relative velocity between inertial reference frames, *''c'' is the ''speed of light in a vacuum'', * is the ratio of ''v'' to ''c'', *''t'' is coordinate time, * is the proper time for an observer (measuring time intervals in the observer's own frame). This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |