|
Transversely Isotropic
A transversely isotropic material is one with physical properties that are symmetric about an axis that is normal to a plane of isotropy. This transverse plane has infinite planes of symmetry and thus, within this plane, the material properties are the same in all directions. Hence, such materials are also known as "polar anisotropic" materials. In geophysics, vertically transverse isotropy (VTI) is also known as radial anisotropy. This type of material exhibits hexagonal symmetry (though technically this ceases to be true for tensors of rank 6 and higher), so the number of independent constants in the (fourth-rank) elasticity tensor are reduced to 5 (from a total of 21 independent constants in the case of a fully anisotropic solid). The (second-rank) tensors of electrical resistivity, permeability, etc. have two independent constants. Example of transversely isotropic materials An example of a transversely isotropic material is the so-called on-axis unidirectional fiber compo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
USA 10052 Grand Canyon Luca Galuzzi 2007
The United States of America (U.S.A. or USA), commonly known as the United States (U.S. or US) or America, is a country Continental United States, primarily located in North America. It consists of 50 U.S. state, states, a Washington, D.C., federal district, five major unincorporated territories, nine United States Minor Outlying Islands, Minor Outlying Islands, and 326 Indian reservations. The United States is also in Compact of Free Association, free association with three Oceania, Pacific Island Sovereign state, sovereign states: the Federated States of Micronesia, the Marshall Islands, and the Palau, Republic of Palau. It is the world's List of countries and dependencies by area, third-largest country by both land and total area. It shares land borders Canada–United States border, with Canada to its north and Mexico–United States border, with Mexico to its south and has maritime borders with the Bahamas, Cuba, Russia, and other nations. With a population of over 333 m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Displacement
In physics, the electric displacement field (denoted by D) or electric induction is a vector field that appears in Maxwell's equations. It accounts for the effects of free and bound charge within materials. "D" stands for "displacement", as in the related concept of displacement current in dielectrics. In free space, the electric displacement field is equivalent to flux density, a concept that lends understanding of Gauss's law. In the International System of Units (SI), it is expressed in units of coulomb per meter square (C⋅m−2). Definition In a dielectric material, the presence of an electric field E causes the bound charges in the material (atomic nuclei and their electrons) to slightly separate, inducing a local electric dipole moment. The electric displacement field "D" is defined as \mathbf \equiv \varepsilon_ \mathbf + \mathbf, where \varepsilon_ is the vacuum permittivity (also called permittivity of free space), and P is the (macroscopic) density of the pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Diffusivity
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of 16 mm2/s, and in water its diffusion coefficient is 0.0016 mm2/s. Diffusivity has dimensions of length2 / time, or m2/s in SI units and cm2/s in CGS units. Temperature dependence of the diffusion coefficient Solids The diffusion coefficient in solids at different temperatures is generally found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concentration Gradient
Molecular diffusion, often simply called diffusion, is the thermal motion of all (liquid or gas) particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size (mass) of the particles. Diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a phase with uniform temperature, absent external net forces acting on the particles, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications to physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface. Terminology The word ''flux'' comes from Latin: ''fluxus'' means "flow", and ''fluere'' is "to flow". As ''fluxion'', this term was introduced into differential calculus by Isaac Newton. The concept of heat flux was a key contribution of Joseph Fourier, in the analysis of heat transfer phenomena. His seminal treatise ''Théorie analytique de la chaleur'' (''The Analytical Theory of Heat''), defines ''fluxion'' as a central quantity and proceeds to derive the now well-known express ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
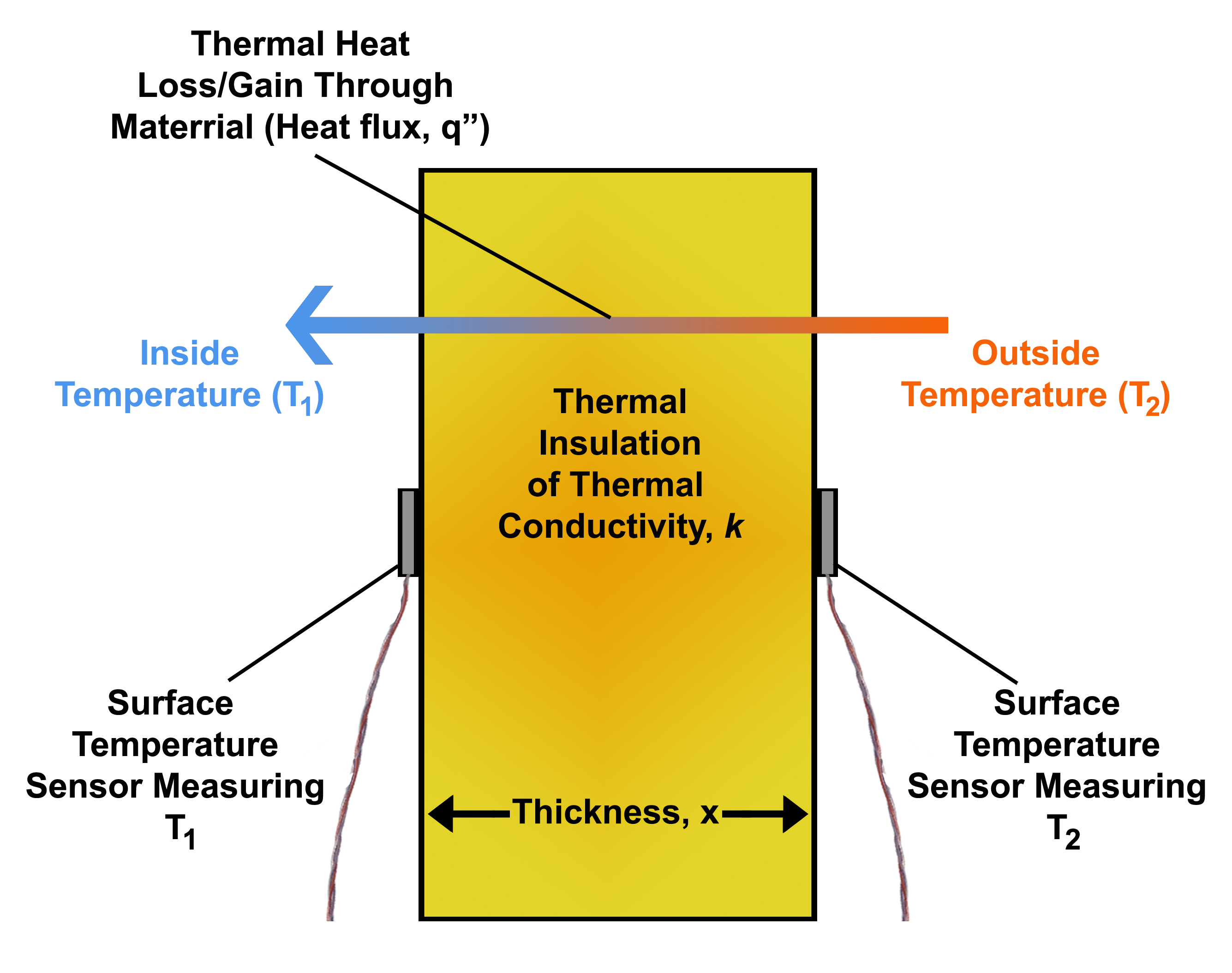
Thermal Conductivity
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by k, \lambda, or \kappa. Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal conductivity. For instance, metals typically have high thermal conductivity and are very efficient at conducting heat, while the opposite is true for insulating materials like Rockwool or Styrofoam. Correspondingly, materials of high thermal conductivity are widely used in heat sink applications, and materials of low thermal conductivity are used as thermal insulation. The reciprocal of thermal conductivity is called thermal resistivity. The defining equation for thermal conductivity is \mathbf = - k \nabla T, where \mathbf is the heat flux, k is the thermal conductivity, and \nabla T is the temperature gradient. This is known as Fourier's Law for heat conduction. Although commonly expressed as a scalar, the most general form of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature Gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature gradient is a dimensional quantity expressed in units of degrees (on a particular temperature scale) per unit length. The SI unit is kelvin per meter (K/m). Temperature gradients in the atmosphere are important in the atmospheric sciences (meteorology, climatology and related fields). Mathematical description Assuming that the temperature ''T'' is an intensive quantity, i.e., a single-valued, continuous and differentiable function of three-dimensional space (often called a scalar field), i.e., that :T=T(x,y,z) where ''x'', ''y'' and ''z'' are the coordinates of the location of interest, then the temperature gradient is the vector quantity defined as :\nabla T = \begin , , \end Physical processes Climatology On a global and annual basis, the dynamics of the atmosphere (and the oceans) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Flux
Heat flux or thermal flux, sometimes also referred to as ''heat flux density'', heat-flow density or ''heat flow rate intensity'' is a flow of energy per unit area per unit time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''mass'' or ''momentum'' flux. Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi_\text = -k \frac where k is the thermal conductivity. The negative sign shows that heat flux moves from higher temperature regions to lower temperature regions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Conduction
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its ''thermal conductivity'', and is denoted . Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform. In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which may be separated spatially. Heat can also be transferred by a combination of conduction and radiation. In solids, conduction is mediated by the combination of vibrations and collisions of molecul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Permeability
In electromagnetism, permeability is the measure of magnetization that a material obtains in response to an applied magnetic field. Permeability is typically represented by the (italicized) Greek letter ''μ''. The term was coined by William Thomson, 1st Baron Kelvin in 1872, and used alongside permittivity by Oliver Heaviside in 1885. The reciprocal of permeability is magnetic reluctivity. In SI units, permeability is measured in henries per meter (H/m), or equivalently in newtons per ampere squared (N/A2). The permeability constant ''μ''0, also known as the magnetic constant or the permeability of free space, is the proportionality between magnetic induction and magnetizing force when forming a magnetic field in a classical vacuum. A closely related property of materials is magnetic susceptibility, which is a dimensionless proportionality factor that indicates the degree of magnetization of a material in response to an applied magnetic field. Explanation In the ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, and are created by electric currents such as those used in electromagnets, and by electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function assigning a vector to each point of space, cal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |