|
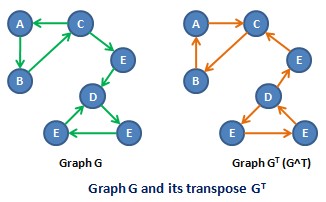
Transpose Graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of Vertex (graph theory), vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa. Notation The name arises because the reversal of arrows corresponds to taking the Converse (logic), converse of an implication in logic. The name is because the adjacency matrix of the transpose directed graph is the transpose of the adjacency matrix of the original directed graph. There is no general agreement on preferred terminology. The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation. Applications Although there is little difference mathematically between a graph and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Strongly Connected Component
In the mathematics, mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachability, reachable from every other vertex. The strongly connected components of a directed graph form a partition of a set, partition into subgraph (graph theory), subgraphs that are themselves strongly connected. It is possible to test the strong connectivity (graph theory), connectivity of a graph, or to find its strongly connected components, in linear time (that is, Θ(''V'' + ''E'')). Definitions A directed graph is called strongly connected if there is a path (graph theory), path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first. In a directed graph ''G'' that may not itself be strongly connected, a pair of vertices ''u'' and ''v'' are said to be strongly connected to each other if there is a path in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are also called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph, each edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transitive Closure
In mathematics, the transitive closure of a homogeneous binary relation on a set (mathematics), set is the smallest Relation (mathematics), relation on that contains and is Transitive relation, transitive. For finite sets, "smallest" can be taken in its usual sense, of having the fewest related pairs; for infinite sets is the unique minimal element, minimal transitive superset of . For example, if is a set of airports and means "there is a direct flight from airport to airport " (for and in ), then the transitive closure of on is the relation such that means "it is possible to fly from to in one or more flights". More formally, the transitive closure of a binary relation on a set is the smallest (w.r.t. ⊆) transitive relation on such that ⊆ ; see . We have = if, and only if, itself is transitive. Conversely, transitive reduction adduces a minimal relation from a given relation such that they have the same closure, that is, ; however, many differen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partial Order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable. Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set (poset for short) is an ordered pair P=(X,\leq) consisting of a set X (called the ''ground set'' of P) and a partial order \leq on X. When the meaning is clear from context and there is no ambiguity about the partial order, the set X itself is sometimes called a poset. Partial order relations The term ''partial order'' usually refers to the reflexive partial order relations, referred to in this article as ''non-strict'' partial orders. However som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Duality (order Theory)
In the mathematical area of order theory, every partially ordered set ''P'' gives rise to a dual (or opposite) partially ordered set which is often denoted by ''P''op or ''P''''d''. This dual order ''P''op is defined to be the same set, but with the inverse order, i.e. ''x'' ≤ ''y'' holds in ''P''op if and only if ''y'' ≤ ''x'' holds in ''P''. It is easy to see that this construction, which can be depicted by flipping the Hasse diagram for ''P'' upside down, will indeed yield a partially ordered set. In a broader sense, two partially ordered sets are also said to be duals if they are dually isomorphic, i.e. if one poset is order isomorphic to the dual of the other. The importance of this simple definition stems from the fact that every definition and theorem of order theory can readily be transferred to the dual order. Formally, this is captured by the Duality Principle for ordered sets: : If a given statement is valid for all partially ordered sets, then its dual statement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs (x, y), where x is an element of X and y is an element of Y. It encodes the common concept of relation: an element x is ''related'' to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. An example of a binary relation is the "divides" relation over the set of prime numbers \mathbb and the set of integers \mathbb, in which each prime p is related to each integer z that is a Divisibility, multiple of p, but not to an integer that is not a Multiple (mathematics), multiple of p. In this relation, for instance, the prime number 2 is related to numbers such as -4, 0, 6, 10, but not to 1 or 9, just as the prime number 3 is related to 0, 6, and 9, but not to 4 or 13. Binary relations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Converse Relation
In mathematics, the converse of a binary relation is the relation that occurs when the order of the elements is switched in the relation. For example, the converse of the relation 'child of' is the relation 'parent of'. In formal terms, if X and Y are sets and L \subseteq X \times Y is a relation from X to Y, then L^ is the relation defined so that yL^x if and only if xLy. In set-builder notation, :L^ = \. Since a relation may be represented by a logical matrix, and the logical matrix of the converse relation is the transpose of the original, the converse relation is also called the transpose relation. It has also been called the opposite or dual of the original relation, the inverse of the original relation,Gerard O'Regan (2016): ''Guide to Discrete Mathematics: An Accessible Introduction to the History, Theory, Logic and Applications'' or the reciprocal L^ of the relation L. Other notations for the converse relation include L^, L^, \breve, L^, or L^. The notati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Isomorphism
In graph theory, an isomorphism of graphs ''G'' and ''H'' is a bijection between the vertex sets of ''G'' and ''H'' : f \colon V(G) \to V(H) such that any two vertices ''u'' and ''v'' of ''G'' are adjacent in ''G'' if and only if f(u) and f(v) are adjacent in ''H''. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection. If an isomorphism exists between two graphs, then the graphs are called isomorphic, often denoted by G\simeq H. In the case when the isomorphism is a mapping of a graph onto itself, i.e., when ''G'' and ''H'' are one and the same graph, the isomorphism is called an automorphism of ''G''. Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to each other is called an isomorphism class of graphs. The question of whether graph isomorphism can be dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Skew-symmetric Graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is graph isomorphism, isomorphic to its own transpose graph, the graph formed by reversing all of its edges, under an isomorphism that is an involution (mathematics), involution without any Fixed point (mathematics), fixed points. Skew-symmetric graphs are identical to the Bipartite double cover, double covering graphs of bidirected graphs. Skew-symmetric graphs were first introduced under the name of ''antisymmetrical digraphs'' by , later as the double covering graphs of polar graphs by , and still later as the double covering graphs of bidirected graphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding Matching (graph theory), matchings in graphs, in testing whether a still life (cellular automaton), still life pattern in Conway's Game of Life may be partitioned into simpler components, in graph drawing, and in the implication gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Depth-first Search
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. Extra memory, usually a stack, is needed to keep track of the nodes discovered so far along a specified branch which helps in backtracking of the graph. A version of depth-first search was investigated in the 19th century by French mathematician Charles Pierre Trémaux as a strategy for solving mazes. Properties The time and space analysis of DFS differs according to its application area. In theoretical computer science, DFS is typically used to traverse an entire graph, and takes time where , V, is the number of vertices and , E, the number of edges. This is linear in the size of the graph. In these applications it also uses space O(, V, ) in the worst case to store the stack of vertices on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kosaraju's Algorithm
In computer science, Kosaraju-Sharir's algorithm (also known as Kosaraju's algorithm) is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph (the same graph with the direction of every edge reversed) has exactly the same strongly connected components as the original graph. The algorithm The primitive graph operations that the algorithm uses are to enumerate the vertices of the graph, to store data per vertex (if not in the graph data structure itself, then in some table that can use vertices as indices), to enumerate the out-neighbours of a vertex (traverse edges in the forward direction), and to enumerate the in-neighbours of a vertex (traverse edges in the backward direction); however the last can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |