|
Total Sum Of Squares
In statistical data analysis the total sum of squares (TSS or SST) is a quantity that appears as part of a standard way of presenting results of such analyses. For a set of observations, y_i, i\leq n, it is defined as the sum over all squared differences between the observations and their overall mean \bar.:Everitt, B.S. (2002) ''The Cambridge Dictionary of Statistics'', CUP, :\mathrm=\sum_^\left(y_-\bar\right)^2 For wide classes of linear models, the total sum of squares equals the explained sum of squares plus the residual sum of squares. For proof of this in the multivariate OLS case, see partitioning in the general OLS model. In analysis of variance (ANOVA) the total sum of squares is the sum of the so-called "within-samples" sum of squares and "between-samples" sum of squares, i.e., partitioning of the sum of squares. In multivariate analysis of variance (MANOVA) the following equation applies Especially chapters 11 and 12. :\mathbf = \mathbf + \mathbf, where T is the to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the ''sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the ''population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of mean are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called '' simple linear regression''; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regression focuses on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Explained Sum Of Squares
In statistics, the explained sum of squares (ESS), alternatively known as the model sum of squares or sum of squares due to regression (SSR – not to be confused with the residual sum of squares (RSS) or sum of squares of errors), is a quantity used in describing how well a model, often a regression model, represents the data being modelled. In particular, the explained sum of squares measures how much variation there is in the modelled values and this is compared to the total sum of squares (TSS), which measures how much variation there is in the observed data, and to the residual sum of squares, which measures the variation in the error between the observed data and modelled values. Definition The explained sum of squares (ESS) is the sum of the squares of the deviations of the predicted values from the mean value of a response variable, in a standard regression model — for example, , where ''y''''i'' is the ''i'' th observation of the response variable, ''x''''ji'' is the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residual Sum Of Squares
In statistics, the residual sum of squares (RSS), also known as the sum of squared estimate of errors (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model, such as a linear regression. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection. In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model. One explanatory variable In a model with a single explanatory variable, RSS is given by: :\operatorname = \sum_^n (y_i - f(x_i))^2 where ''y''''i'' is the ''i''th value of the variable to be predicted, ''x''''i'' is the ''i''th value of the explanatory variable, and f(x_i) is the predicted value of ''y''''i'' (also te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Explained Sum Of Squares
In statistics, the explained sum of squares (ESS), alternatively known as the model sum of squares or sum of squares due to regression (SSR – not to be confused with the residual sum of squares (RSS) or sum of squares of errors), is a quantity used in describing how well a model, often a regression model, represents the data being modelled. In particular, the explained sum of squares measures how much variation there is in the modelled values and this is compared to the total sum of squares (TSS), which measures how much variation there is in the observed data, and to the residual sum of squares, which measures the variation in the error between the observed data and modelled values. Definition The explained sum of squares (ESS) is the sum of the squares of the deviations of the predicted values from the mean value of a response variable, in a standard regression model — for example, , where ''y''''i'' is the ''i'' th observation of the response variable, ''x''''ji'' is the '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Analysis Of Variance
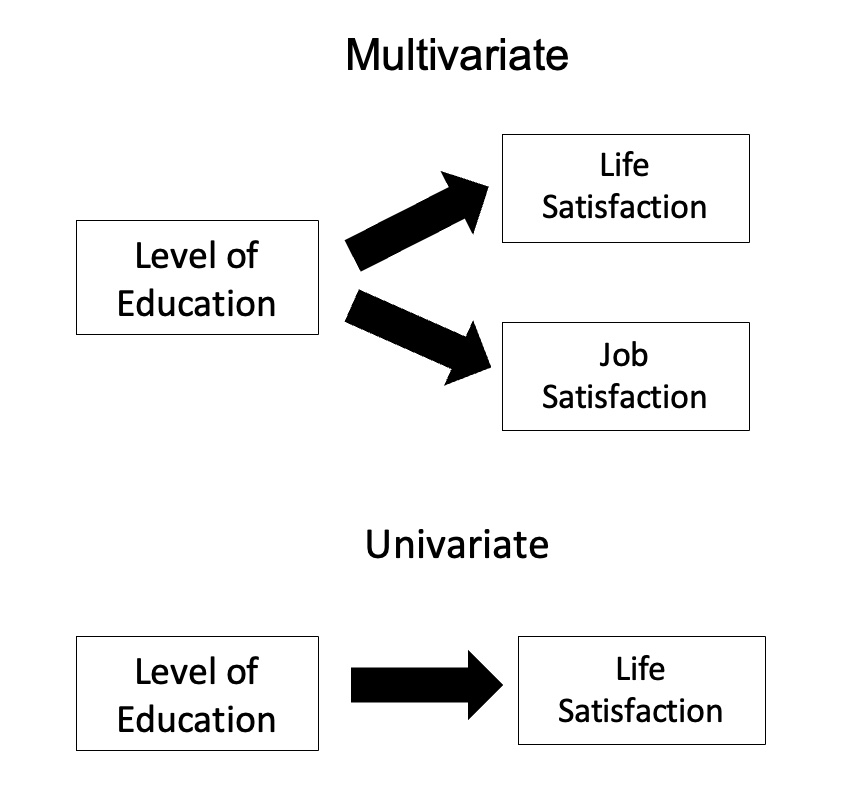
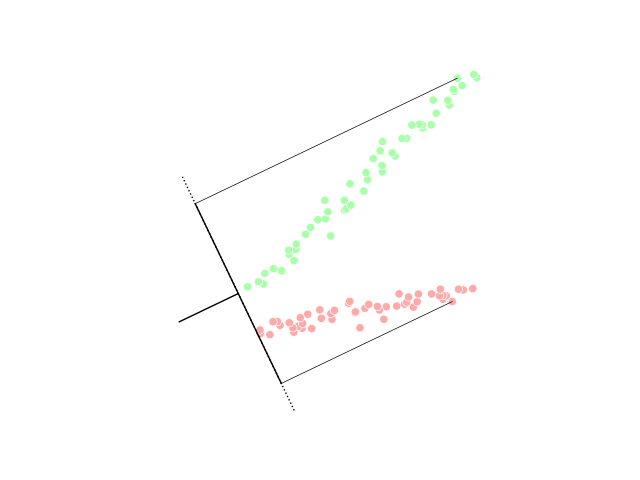
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately. Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers. Relationship with ANOVA MANOVA is a generalized form of univariate analysis of variance (ANOVA), although, unlike univariate ANOVA, it uses the covariance between outcome variables in testing the statistical significance of the mean differences. Where sums o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Academic Press
Academic Press (AP) is an academic book publisher founded in 1941. It was acquired by Harcourt, Brace & World in 1969. Reed Elsevier bought Harcourt in 2000, and Academic Press is now an imprint of Elsevier. Academic Press publishes reference books, serials and online products in the subject areas of: * Communications engineering * Economics * Environmental science * Finance * Food science and nutrition * Geophysics * Life sciences * Mathematics and statistics * Neuroscience * Physical sciences * Psychology Well-known products include the ''Methods in Enzymology'' series and encyclopedias such as ''The International Encyclopedia of Public Health'' and the ''Encyclopedia of Neuroscience''. See also * Akademische Verlagsgesellschaft (AVG) — the German predecessor, founded in 1906 by Leo Jolowicz (1868–1940), the father of Walter Jolowicz Walter may refer to: People * Walter (name), both a surname and a given name * Little Walter, American blues harmonica player Marion Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squared Deviations From The Mean
Squared deviations from the mean (SDM) result from squaring deviations. In probability theory and statistics, the definition of ''variance'' is either the expected value of the SDM (when considering a theoretical distribution) or its average value (for actual experimental data). Computations for ''analysis of variance'' involve the partitioning of a sum of SDM. Background An understanding of the computations involved is greatly enhanced by a study of the statistical value : \operatorname( X ^ 2 ), where \operatorname is the expected value operator. For a random variable X with mean \mu and variance \sigma^2, : \sigma^2 = \operatorname( X ^ 2 ) - \mu^2.Mood & Graybill: ''An introduction to the Theory of Statistics'' (McGraw Hill) Therefore, : \operatorname( X ^ 2 ) = \sigma^2 + \mu^2. From the above, the following can be derived: : \operatorname\left( \sum\left( X ^ 2\right) \right) = n\sigma^2 + n\mu^2, : \operatorname\left( \left(\sum X \right)^ 2 \right) = n\sigma^2 + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |