|
Time–frequency Analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains ''simultaneously,'' using various time–frequency representations. Rather than viewing a 1-dimensional signal (a function, real or complex-valued, whose domain is the real line) and some transform (another function whose domain is the real line, obtained from the original via some transform), time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform. The mathematical motivation for this study is that functions and their transform representation are tightly connected, and they can be understood better by studying them jointly, as a two-dimensional object, rather than separately. A simple example is that the 4-fold periodicity of the Fourier transform – and the fact that two-fold Fourier transform reverses direction – can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, subjective video quality and to also detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was published in the Bell System Technical Journal. The paper laid the groundwork for later development of information c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Wigner Distribution Function
:''Note: the Wigner distribution function is abbreviated here as WD rather than WDF as used at Wigner distribution function'' A Modified Wigner distribution function is a variation of the Wigner distribution function (WD) with reduced or removed cross-terms. The Wigner distribution (WD) was first proposed for corrections to classical statistical mechanics in 1932 by Eugene Wigner. The Wigner distribution function, or Wigner–Ville distribution (WVD) for analytic signals, also has applications in time frequency analysis. The Wigner distribution gives better auto term localisation compared to the smeared out spectrogram (SP). However, when applied to a signal with multi frequency components, cross terms appear due to its quadratic nature. Several methods have been proposed to reduce the cross terms. For example, in 1994 L. Stankovic proposed a novel technique, now mostly referred to as S-method, resulting in the reduction or removal of cross terms. The concept of the S-method i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter Tf
Filter, filtering or filters may refer to: Science and technology Computing * Filter (higher-order function), in functional programming * Filter (software), a computer program to process a data stream * Filter (video), a software component that performs some operation on a multimedia stream * Email filtering, the processing of email to organize it according to specified criteria * Content-control software also known as an Internet filter * Wordfilter, a script typically used on Internet forums or chat rooms * Berkeley Packet Filter, filter expression used in the qualification of network data * DSL filter, a low-pass filter installed between analog devices and a telephone line * Helicon Filter, a raster graphics editor * Filter (large eddy simulation), a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations * Kalman filter, an approximating algorithm in optimal control applications and problems Device * Filter (che ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
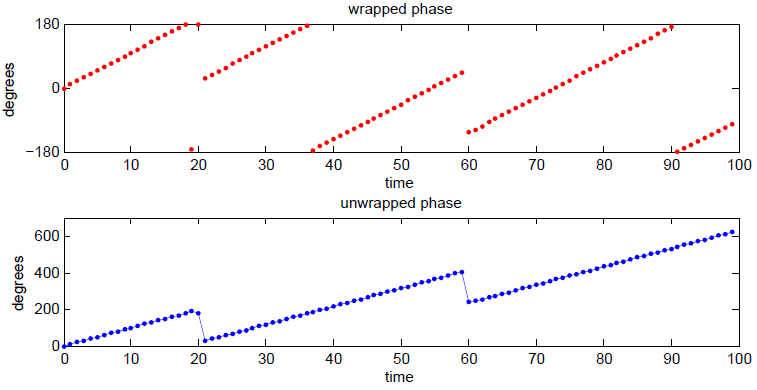
Instantaneous Phase
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instantaneous Frequency
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Fourier Transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform (FRFT) is a family of linear transformations generalizing the Fourier transform. It can be thought of as the Fourier transform to the ''n''-th power, where ''n'' need not be an integer — thus, it can transform a function to any ''intermediate'' domain between time and frequency. Its applications range from filter design and signal analysis to phase retrieval and pattern recognition. The FRFT can be used to define fractional convolution, correlation, and other operations, and can also be further generalized into the linear canonical transformation (LCT). An early definition of the FRFT was introduced by Condon, by solving for the Green's function for phase-space rotations, and also by Namias, generalizing work of Wiener on Hermite polynomials. However, it was not widely recognized in signal processing until it was independently reintroduced around 1993 by several groups. Since then, there h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Canonical Transform
In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms. It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). As this defines the original function up to a sign, this translates into an action of its double cover on the original function space. The LCT generalizes the Fourier, fractional Fourier, Laplace, Gauss–Weierstrass, Bargmann and the Fresnel transforms as particular cases. The name "linear canonical transformation" is from canonical transformation, a map that preserves the symplectic structure, as SL2(R) can also be interpreted as the symplectic group Sp2, and thus LCTs are the linear maps of the time–frequency domain which preserve the symplectic form, and their action on the Hilbert space is given by the Metaplectic group. The basic properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter Design For White Noise
Filter, filtering or filters may refer to: Science and technology Computing * Filter (higher-order function), in functional programming * Filter (software), a computer program to process a data stream * Filter (video), a software component that performs some operation on a multimedia stream * Email filtering, the processing of email to organize it according to specified criteria * Content-control software also known as an Internet filter * Wordfilter, a script typically used on Internet forums or chat rooms * Berkeley Packet Filter, filter expression used in the qualification of network data * DSL filter, a low-pass filter installed between analog devices and a telephone line * Helicon Filter, a raster graphics editor * Filter (large eddy simulation), a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations * Kalman filter, an approximating algorithm in optimal control applications and problems Device * Filter (che ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Random Process's WDF And AF
In addition to its common meaning, stationary may have the following specialized scientific meanings: Mathematics * Stationary point * Stationary process * Stationary state Meteorology * A stationary front is a weather front that is not moving Physics * A time-invariant system quantity, such as a constant position or temperature * A steady state physical process, such as a vibration at constant amplitude and frequency or a steady fluid flow * A stationary wave is a standing wave In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect ... * Stationary spacetime in general relativity Other uses * "Stationary", a song from ''Copacetic'' (Knuckle Puck album) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Process
In mathematics and statistics, a stationary process (or a strict/strictly stationary process or strong/strongly stationary process) is a stochastic process whose unconditional joint probability distribution does not change when shifted in time. Consequently, parameters such as mean and variance also do not change over time. If you draw a line through the middle of a stationary process then it should be flat; it may have 'seasonal' cycles, but overall it does not trend up nor down. Since stationarity is an assumption underlying many statistical procedures used in time series analysis, non-stationary data are often transformed to become stationary. The most common cause of violation of stationarity is a trend in the mean, which can be due either to the presence of a unit root or of a deterministic trend. In the former case of a unit root, stochastic shocks have permanent effects, and the process is not mean-reverting. In the latter case of a deterministic trend, the process is called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambiguity Function
In pulsed radar and sonar signal processing, an ambiguity function is a two-dimensional function of propagation delay \tau and Doppler frequency f, \chi(\tau,f). It represents the distortion of a returned pulse due to the receiver matched filter (commonly, but not exclusively, used in pulse compression radar) of the return from a moving target. The ambiguity function is defined by the properties of the pulse and of the filter, and not any particular target scenario. Many definitions of the ambiguity function exist; some are restricted to narrowband signals and others are suitable to describe the delay and Doppler relationship of wideband signals. Often the definition of the ambiguity function is given as the magnitude squared of other definitions (WeissWeiss, Lora G. "Wavelets and Wideband Correlation Processing". ''IEEE Signal Processing Magazine'', pp. 13–32, Jan 1994). For a given complex baseband pulse s(t), the narrowband ambiguity function is given by :\chi(\tau,f)=\int_^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone-shape Distribution Function
The cone-shape distribution function, also known as the Zhao–Atlas–Marks time-frequency distribution,Leon Cohen, Time Frequency Analysis: Theory and Applications, Prentice Hall, (1994) (acronymized as the ZAM distribution or ZAMD), is one of the members of Cohen's class distribution function. It was first proposed by Yunxin Zhao, Les E. Atlas, and Robert J. Marks II in 1990. The distribution's name stems from the twin cone shape of the distribution's kernel function on the t, \tau plane. The advantage of the cone kernel function is that it can completely remove the cross-term between two components having the same center frequency. Cross-term results from components with the same time center, however, cannot be completely removed by the cone-shaped kernel. Mathematical definition The definition of the cone-shape distribution function is: :C_x(t, f)=\int_^\int_^A_x(\eta,\tau)\Phi(\eta,\tau)\exp (j2\pi(\eta t-\tau f))\, d\eta\, d\tau, where :A_x(\eta,\tau)=\int_^x(t+\tau / ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
