|
Trigonometric Integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth spherical Bessel function. Since is an even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of the sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency dom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plot Of The Hyperbolic Sine Integral Function Shi(z) In The Complex Plane From -2-2i To 2+2i With Colors Created With Mathematica 13
Plot or Plotting may refer to: Art, media and entertainment * Plot (narrative), the story of a piece of fiction Music * ''The Plot'' (album), a 1976 album by jazz trumpeter Enrico Rava * The Plot (band), a band formed in 2003 Other * ''Plot'' (film), a 1973 French-Italian film * ''Plotting'' (video game), a 1989 Taito puzzle video game, also called Flipull * ''The Plot'' (video game), a platform game released in 1988 for the Amstrad CPC and Sinclair Spectrum * ''Plotting'' (non-fiction), a 1939 book on writing by Jack Woodford * ''The Plot'' (novel), a 2021 mystery by Jean Hanff Korelitz Graphics * Plot (graphics), a graphical technique for representing a data set * Plot (radar), a graphic display that shows all collated data from a ship's on-board sensors * Plot plan, a type of drawing which shows existing and proposed conditions for a given area Land * Plot (land), a piece of land used for building on ** Burial plot, a piece of land a person is buried in * Quadrat, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Integral
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line: : \int_0^\infty \frac \,dx = \frac. This integral is not absolutely convergent, meaning \Biggl, \frac \Biggl, is not Lebesgue-integrable, and so the Dirichlet integral is undefined in the sense of Lebesgue integration. It is, however, defined in the sense of the improper Riemann integral or the generalized Riemann or Henstock–Kurzweil integral. This can be seen by using Dirichlet's test for improper integrals. Although the sine integral, an antiderivative of the sinc function, is not an elementary function, the value of the integral (in the Riemann or Henstock sense) can be derived using various ways, including the Laplace transform, double integration, differentiating under the integral sign, contour integration, and the Dirichlet kernel. Eva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosine Integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth spherical Bessel function. Since is an even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of the sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency domain r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''period''), the number of components, and their amplitudes and phase parameters. With appropriate choices, one cycle (or ''period'') of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic). The number of components is theoretically infinite, in which case the other parameters can be chosen to cause the series to converge to almost any ''well behaved'' periodic function (see Pathological and Dirichlet–Jordan test). The components of a particular function are determined by ''analysis'' techniques described in this article. Sometimes the components are known first, and the unknown function is ''synthesized'' by a Fourier series. Such is the case of a discrete- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heaviside Step Function
The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , or ), is a step function, named after Oliver Heaviside (1850–1925), the value of which is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as . The Heaviside function may be defined as: * a piecewise function: H(x) := \begin 1, & x > 0 \\ 0, & x \le 0 \end * using the Iverson bracket notation: H(x) := 0.html" ;"title=">0">>0/math> * an indicator function: H(x) := \mathbf_=\mathbf 1_(x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions ( and ) that produces a third function (f*g) that expresses how the shape of one is modified by the other. The term ''convolution'' refers to both the result function and to the process of computing it. It is defined as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). The integral is evaluated for all values of shift, producing the convolution function. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution (f*g) differs from cross-correlation (f \star g) only in that either or is reflected about the y-axis in convolution; thus it is a cross-correlation of and , or and . For complex-valued fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Phenomenon
In mathematics, the Gibbs phenomenon, discovered by Available on-line at:National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979. and rediscovered by , is the oscillatory behavior of the Fourier series of a piecewise continuously differentiable periodic function around a jump discontinuity. The function's Nth partial Fourier series (formed by summing its N lowest constituent sinusoids) produces large peaks around the jump which overshoot and undershoot the function's actual values. This approximation error approaches a limit of about 9% of the jump as more sinusoids are used, though the infinite Fourier series sum does eventually converge almost everywhere except the point of discontinuity. The Gibbs phenomenon was observed by experimental physicists, but was believed to be due to imperfections in the measuring apparatus, and it is one cause of ringing artifacts in signal processing. Description The Gibbs phenomenon involves both the fact that Fourier sums ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Low-pass Filter
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter design. The filter is sometimes called a high-cut filter, or treble-cut filter in audio applications. A low-pass filter is the complement of a high-pass filter. In optics, high-pass and low-pass may have different meanings, depending on whether referring to frequency or wavelength of light, since these variables are inversely related. High-pass frequency filters would act as low-pass wavelength filters, and vice versa. For this reason it is a good practice to refer to wavelength filters as ''short-pass'' and ''long-pass'' to avoid confusion, which would correspond to ''high-pass'' and ''low-pass'' frequencies. Low-pass filters exist in many different forms, including electronic circuits such as a hiss filter used in audio, anti-alia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Domain
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signal changes over time, whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies. A frequency-domain representation can also include information on the phase shift that must be applied to each sinusoid in order to be able to recombine the frequency components to recover the original time signal. A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transform, which converts a time function into a complex valued sum or integral of sine waves of different frequencies, with amplitudes and phases, each of which represents a frequency component. The "spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Filter
In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given cutoff frequency, without affecting lower frequencies, and has linear phase response. The filter's impulse response is a sinc function in the time domain and its frequency response is a rectangular function. It is an "ideal" low-pass filter in the frequency sense, perfectly passing low frequencies, perfectly cutting high frequencies; and thus may be considered to be a ''brick-wall filter''. Real-time filters can only approximate this ideal, since an ideal sinc filter (a.k.a. ''rectangular filter'') is non-causal and has an infinite delay, but it is commonly found in conceptual demonstrations or proofs, such as the sampling theorem and the Whittaker–Shannon interpolation formula. In mathematical terms, the desired frequency response is the rectangular function: :H(f) = \operatorname \left( \frac \right) = \begin 0, & \text , f, > B, \\ \frac, & \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

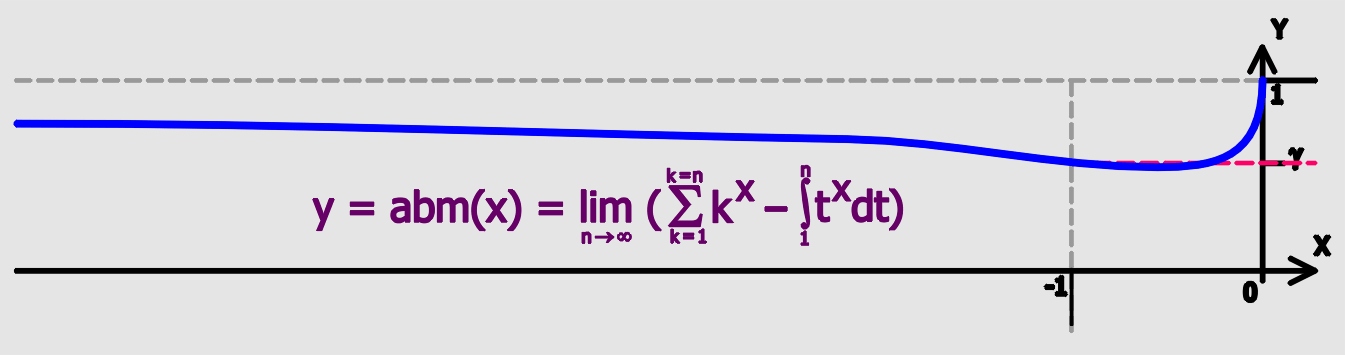

.gif)