|
Ternary
Ternary (from Latin ''ternarius'') or trinary is an adjective meaning "composed of three items". It can refer to: Mathematics and logic * Ternary numeral system, a base-3 counting system ** Balanced ternary, a positional numeral system, useful for comparison logic * Ternary logic, a logic system with the values ''true'', ''false'', and some other value * Ternary plot or ternary graph, a plot that shows the ratios of three proportions * Ternary relation, a finitary relation in which the number of places in the relation is three * Ternary operation, an operation that takes three parameters * Ternary function, a function that takes three arguments Computing * Ternary signal, a signal that can assume three significant values * Ternary computer, a computer using a ternary numeral system * Ternary tree, a tree data structure in computer science ** Ternary search tree, a ternary (three-way) tree data structure of strings * Ternary search, a computer science technique for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Balanced Ternary
Balanced ternary is a ternary numeral system (i.e. base 3 with three digits) that uses a balanced signed-digit representation of the integers in which the digits have the values −1, 0, and 1. This stands in contrast to the standard (unbalanced) ternary system, in which digits have values 0, 1 and 2. The balanced ternary system can represent all integers without using a separate minus sign; the value of the leading non-zero digit of a number has the sign of the number itself. The balanced ternary system is an example of a non-standard positional numeral system. It was used in some early computers and also in some solutions of balance puzzles. Different sources use different glyphs used to represent the three digits in balanced ternary. In this article, T (which resembles a ligature of the minus sign and 1) represents −1, while 0 and 1 represent themselves. Other conventions include using '−' and '+' to represent −1 and 1 respectively, or using Greek letter theta ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Numeral System
A ternary numeral system (also called base 3 or trinary) has three as its base. Analogous to a bit, a ternary digit is a trit (trinary digit). One trit is equivalent to log2 3 (about 1.58496) bits of information. Although ''ternary'' most often refers to a system in which the three digits are all non–negative numbers; specifically , , and , the adjective also lends its name to the balanced ternary system; comprising the digits −1, 0 and +1, used in comparison logic and ternary computers. Comparison to other bases Representations of integer numbers in ternary do not get uncomfortably lengthy as quickly as in binary. For example, decimal 365 or senary 1405 corresponds to binary 101101101 (nine digits) and to ternary 111112 (six digits). However, they are still far less compact than the corresponding representations in bases such as decimalsee below for a compact way to codify ternary using nonary (base 9) and septemvigesimal (base 27). As for rational num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Computer
A ternary computer, also called trinary computer, is one that uses ternary logic (i.e., base 3) instead of the more common binary system (i.e., base 2) in its calculations. This means it uses trits (instead of bits, as most computers do). Types of states Ternary computing deals with three discrete states, but the ternary digits themselves can be defined differently: Ternary quantum computers use qutrits rather than trits. A qutrit is a quantum state that is a complex unit vector in three dimensions, which can be written as , \Psi\rangle = \alpha, 0\rangle + \beta, 1\rangle + \gamma, 2\rangle in the bra-ket notation. The labels given to the basis vectors (, 0\rangle, , 1\rangle, , 2\rangle) can be replaced with other labels, for example those given above. History One early calculating machine, built entirely from wood by Thomas Fowler in 1840, operated in balanced ternary. The first modern, electronic ternary computer, Setun, was built in 1958 in the Soviet Union a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
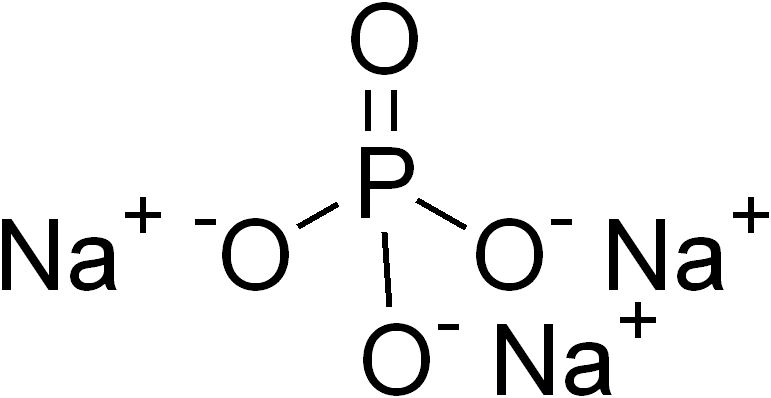
Ternary Compound
In inorganic chemistry and materials chemistry, a ternary compound or ternary phase is a chemical compound containing three different elements. While some ternary compounds are molecular, ''e.g.'' chloroform (), more typically ternary phases refer to extended solids. Famous example are the perovskites. Binary phases, with only two elements, have lower degrees of complexity than ternary phases. With four elements, quaternary phases are more complex. The number of isomers of a ternary compound provide a distinction between inorganic and organic chemistry: "In inorganic chemistry one or, at most, only a few compounds composed of any two or three elements were known, whereas in organic chemistry the situation was very different." Ternary crystalline compounds An example is sodium phosphate, . The sodium ion has a charge of 1+ and the phosphate ion has a charge of 3–. Therefore, three sodium ions are needed to balance the charge of one phosphate ion. Another example of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Search Tree
In computer science, a ternary search tree is a type of trie (sometimes called a ''prefix tree'') where nodes are arranged in a manner similar to a binary search tree, but with up to three children rather than the binary tree's limit of two. Like other prefix trees, a ternary search tree can be used as an associative map structure with the ability for incremental string search. However, ternary search trees are more space efficient compared to standard prefix trees, at the cost of speed. Common applications for ternary search trees include spell-checking and auto-completion. Description Each node of a ternary search tree stores a single character, an object (or a pointer to an object depending on implementation), and pointers to its three children conventionally named ''equal kid'', ''lo kid'' and ''hi kid'', which can also be referred respectively as ''middle (child)'', ''lower (child)'' and ''higher (child)''. A node may also have a pointer to its parent node as well as an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Plot
A ternary plot, ternary graph, triangle plot, simplex plot, Gibbs triangle or de Finetti diagram is a barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle. It is used in physical chemistry, petrology, mineralogy, metallurgy, and other physical sciences to show the compositions of systems composed of three species. In population genetics, a triangle plot of genotype frequencies is called a de Finetti diagram. In game theory, it is often called a simplex plot.Karl Tuyls, "An evolutionary game-theoretic analysis of poker strategies", ''Entertainment Computing'' January 2009 , p. 9 Ternary plots are tools for analyzing compositional data in the three-dimensional case. In a ternary plot, the values of the three variables , , and must sum to some constant, . Usually, this constant is represented as 1.0 or 100%. Because for all substances being graphed, any one variable is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Golay Code
In coding theory, the ternary Golay codes are two closely related error-correcting codes. The code generally known simply as the ternary Golay code is an 1, 6, 53-code, that is, it is a linear code over a ternary alphabet; the relative distance of the code is as large as it possibly can be for a ternary code, and hence, the ternary Golay code is a perfect code. The extended ternary Golay code is a 2, 6, 6linear code obtained by adding a zero-sum check digit to the 1, 6, 5code. In finite group theory, the extended ternary Golay code is sometimes referred to as the ternary Golay code. Properties Ternary Golay code The ternary Golay code consists of 36 = 729 codewords. Its parity check matrix is : \left[ \begin 1 & 1 & 1 & 2 & 2 & 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 2 & 1 & 0 & 2 & 0 & 1 & 0 & 0 & 0\\ 1 & 2 & 1 & 0 & 1 & 2 & 0 & 0 & 1 & 0 & 0\\ 1 & 2 & 0 & 1 & 2 & 1 & 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 2 & 2 & 1 & 1 & 0 & 0 & 0 & 0 & 1 \end \right]. Any two different ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Operation
In mathematics, a ternary operation is an ''n''- ary operation with ''n'' = 3. A ternary operation on a set ''A'' takes any given three elements of ''A'' and combines them to form a single element of ''A''. In computer science, a ternary operator is an operator that takes three arguments as input and returns one output. Examples The function T(a, b, c) = ab + c is an example of a ternary operation on the integers (or on any structure where + and \times are both defined). Properties of this ternary operation have been used to define planar ternary rings in the foundations of projective geometry. In the Euclidean plane with points ''a'', ''b'', ''c'' referred to an origin, the ternary operation , b, c= a - b + c has been used to define free vectors. Since (''abc'') = ''d'' implies ''a'' – ''b'' = ''c'' – ''d'', these directed segments are equipollent and are associated with the same free vector. Any three points in the plane ''a, b, c'' thus determine a parallelogram w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Logic
In logic, a three-valued logic (also trinary logic, trivalent, ternary, or trilean, sometimes abbreviated 3VL) is any of several many-valued logic systems in which there are three truth values indicating ''true'', ''false'' and some indeterminate third value. This is contrasted with the more commonly known bivalent logics (such as classical sentential or Boolean logic) which provide only for ''true'' and ''false''. Emil Leon Post is credited with first introducing additional logical truth degrees in his 1921 theory of elementary propositions. The conceptual form and basic ideas of three-valued logic were initially published by Jan Łukasiewicz and Clarence Irving Lewis. These were then re-formulated by Grigore Constantin Moisil in an axiomatic algebraic form, and also extended to ''n''-valued logics in 1945. Pre-discovery Around 1910, Charles Sanders Peirce defined a many-valued logic system. He never published it. In fact, he did not even number the three pages of notes wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Form
Ternary form, sometimes called song form, is a three-part musical form consisting of an opening section (A), a following section (B) and then a repetition of the first section (A). It is usually schematized as A–B–A. Prominent examples include the da capo aria "The trumpet shall sound" from Handel's ''Messiah'', Chopin's Prelude in D-Flat Major "Raindrop", ( Op. 28) and the opening chorus of Bach's ''St John Passion''. Simple ternary form In ternary form each section is self-contained both thematically as well as tonally (that is, each section contains distinct and complete themes), and ends with an authentic cadence. The B section is generally in a contrasting but closely related key, usually a perfect fifth above or the parallel minor of the home key of the A section (V or i); however, in many works of the Classical period, the B section stays in tonic but has contrasting thematic material. It usually also has a contrasting character; for example section A might be stif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Relation
In mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place. Just as a binary relation is formally defined as a set of ''pairs'', i.e. a subset of the Cartesian product of some sets ''A'' and ''B'', so a ternary relation is a set of triples, forming a subset of the Cartesian product of three sets ''A'', ''B'' and ''C''. An example of a ternary relation in elementary geometry can be given on triples of points, where a triple is in the relation if the three points are collinear. Another geometric example can be obtained by considering triples consisting of two points and a line, where a triple is in the ternary relation if the two points determine (are incident with) the line. Examples Binary functions A function in two variables, mapping two values from sets ''A'' and ''B'', respectively, to a value in ''C'' associat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Tree
: In computer science, a ternary tree is a tree data structure in which each node has at most three child nodes, usually distinguished as "left", “mid” and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to the "root" node (the ancestor of all nodes), if it exists. Any node in the data structure can be reached by starting at root node and repeatedly following references to either the left, mid or right child. Ternary trees are used to implement Ternary search trees and Ternary heaps. Definition * Directed Edge - The link from the parent to the child. * Root - The node with no parents. There is at most one root node in a rooted tree. * Leaf Node - Any node that has no children. * Parent Node - Any node connected by a directed edge to its child or children. * Child Node - Any node connected to a parent node by a directed edge. * Depth - Length of the path from the root to the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |