|
T-value
In statistics, the ''t''-statistic is the ratio of the difference in a number’s estimated value from its assumed value to its Standard error (statistics), standard error. It is used in statistical hypothesis testing, hypothesis testing via Student's t-test, Student's ''t''-test. The ''t''-statistic is used in a ''t''-test to determine whether to support or reject the null hypothesis. It is very similar to the Standard score, z-score but with the difference that ''t''-statistic is used when the sample size is small or the population standard deviation is unknown. For example, the ''t''-statistic is used in estimating the population mean from a sampling distribution of sample means if the population standard deviation is unknown. It is also used along with p-value when running hypothesis tests where the p-value tells us what the odds are of the results to have happened. Definition and features Let \hat\beta be an estimator of parameter ''β'' in some statistical model. Then a ''t' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-value
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely ''under the null hypothesis''. Even though reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields, misinterpretation and misuse of p-values is widespread and has been a major topic in mathematics and metascience. In 2016, the American Statistical Association (ASA) made a formal statement that "''p''-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone" and that "a ''p''-value, or statistical significance, does not measure the size of an effect or the importance of a result" or "evidence regarding a model or hypothesis". That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Dickey–Fuller Test
In statistics, an augmented Dickey–Fuller test (ADF) tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis depends on which version of the test is used, but is usually stationarity or trend-stationarity. It is an augmented version of the Dickey–Fuller test for a larger and more complicated set of time series models. The augmented Dickey–Fuller (ADF) statistic, used in the test, is a negative number. The more negative it is, the stronger the rejection of the hypothesis that there is a unit root at some level of confidence. Testing procedure The procedure for the ADF test is the same as for the Dickey–Fuller test but it is applied to the model :\Delta y_t = \alpha + \beta t + \gamma y_ + \delta_1 \Delta y_ + \cdots + \delta_ \Delta y_ + \varepsilon_t, where \alpha is a constant, \beta the coefficient on a time trend and p the lag order of the autoregressive process. Imposing the constraints \alpha = 0 and \beta = 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-distribution
In probability theory and statistics, Student's distribution (or simply the distribution) t_\nu is a continuous probability distribution that generalizes the Normal distribution#Standard normal distribution, standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped. However, t_\nu has Heavy-tailed distribution, heavier tails, and the amount of probability mass in the tails is controlled by the parameter \nu. For \nu = 1 the Student's distribution t_\nu becomes the standard Cauchy distribution, which has very fat-tailed distribution, "fat" tails; whereas for \nu \to \infty it becomes the standard normal distribution \mathcal(0, 1), which has very "thin" tails. The name "Student" is a pseudonym used by William Sealy Gosset in his scientific paper publications during his work at the Guinness Brewery in Dublin, Ireland. The Student's distribution plays a role in a number of widely used statistical analyses, including Student's t- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prediction Interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval (statistics), interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis. A simple example is given by a six-sided die with face values ranging from 1 to 6. The confidence interval for the estimated expected value of the face value will be around 3.5 and will become narrower with a larger sample size. However, the prediction interval for the next roll will approximately range from 1 to 6, even with any number of samples seen so far. Prediction intervals are used in both frequentist statistics and Bayesian statistics: a prediction interval bears the same relationship to a future observation that a frequentist confidence interval or Bayesian credible interval bears to an unobservable population parameter: prediction intervals predict the distribution of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancillary Statistic
In statistics, ancillarity is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. An ancillary statistic has the same distribution regardless of the value of the parameters and thus provides no information about them. It is opposed to the concept of a complete statistic which contains no ancillary information. It is closely related to the concept of a sufficient statistic which contains all of the information that the dataset provides about the parameters. A ancillary statistic is a specific case of a pivotal quantity that is computed only from the data and not from the parameters. They can be used to construct prediction intervals. They are also used in connection with Basu's theorem to prove independence between statistics. This concept was first introduced by Ronald Fisher in the 1920s, but its formal definition was only provided in 1964 by Debabrata Basu. Examples Suppose ''X''1, ..., ''X''''n'' are independent a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z-score
In statistics, the standard score or ''z''-score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores. It is calculated by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation. This process of converting a raw score into a standard score is called standardizing or normalizing (however, "normalizing" can refer to many types of ratios; see ''Normalization'' for more). Standard scores are most commonly called ''z''-scores; the two terms may be used interchangeably, as they are in this article. Other equivalent terms in use include z-value, z-statistic, normal score, standardized variable and pull in high energy physics. Computing a z-score requires knowledge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pivotal Quantity
In statistics, a pivotal quantity or pivot is a function of observations and unobservable parameters such that the function's probability distribution does not depend on the unknown parameters (including nuisance parameters). A pivot need not be a statistic — the function and its can depend on the parameters of the model, but its must not. If it is a statistic, then it is known as an ''ancillary statistic''. More formally, let X = (X_1,X_2,\ldots,X_n) be a random sample from a distribution that depends on a parameter (or vector of parameters) \theta . Let g(X,\theta) be a random variable whose distribution is the same for all \theta . Then g is called a ''pivotal quantity'' (or simply a ''pivot''). Pivotal quantities are commonly used for Normalization (statistics), normalization to allow data from different data sets to be compared. It is relatively easy to construct pivots for location and scale parameters: for the former we form differences so that location cancels, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
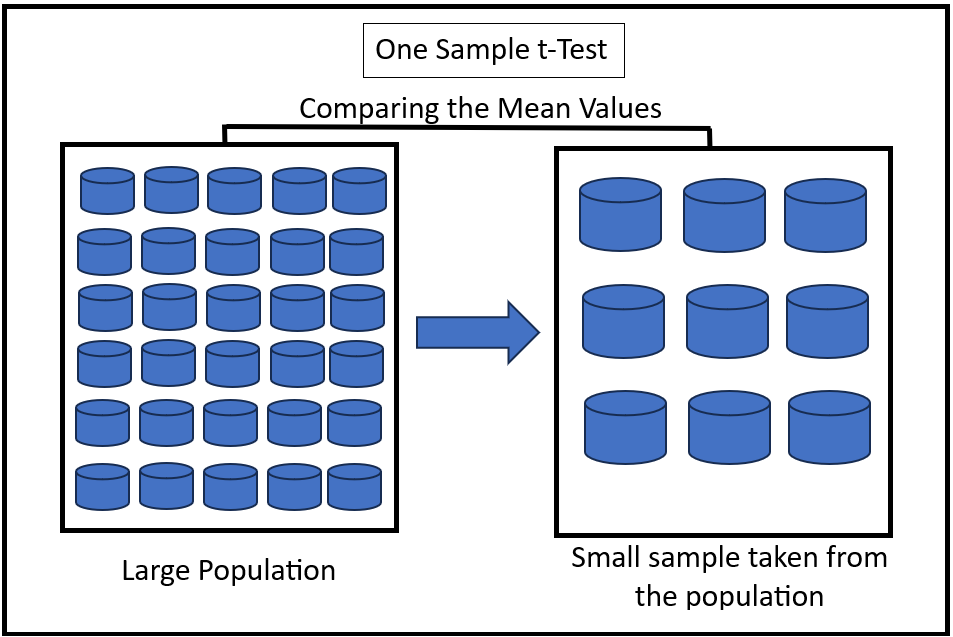
Student's T Test
Student's ''t''-test is a statistical test used to test whether the difference between the response of two groups is statistically significant or not. It is any statistical hypothesis test in which the test statistic follows a Student's ''t''-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known (typically, the scaling term is unknown and is therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's ''t'' distribution. The ''t''-test's most common application is to test whether the means of two populations are significantly different. In many cases, a ''Z''-test will yield very similar results to a ''t''-test because the latter converges to the former as the size of the dataset increases. History The term "''t''-statistic" is abbreviated from "hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Root
In probability theory and statistics, a unit root is a feature of some stochastic processes (such as random walks) that can cause problems in statistical inference involving time series models. A linear stochastic process has a unit root if 1 is a root of the process's characteristic equation. Such a process is non-stationary but does not always have a trend. If the other roots of the characteristic equation lie inside the unit circle—that is, have a modulus (absolute value) less than one—then the first difference of the process will be stationary; otherwise, the process will need to be differenced multiple times to become stationary. If there are ''d'' unit roots, the process will have to be differenced ''d'' times in order to make it stationary. Due to this characteristic, unit root processes are also called difference stationary. Unit root processes may sometimes be confused with trend-stationary processes; while they share many properties, they are different in m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |